What Is Congruent in geometry? This concept refers to figures being identical in shape and size. At WHAT.EDU.VN, we aim to demystify this fundamental idea with clear explanations and practical examples. Explore geometric congruence, coinciding shapes, and equal figures with us!
1. Delving Into Congruent Meaning in Geometry
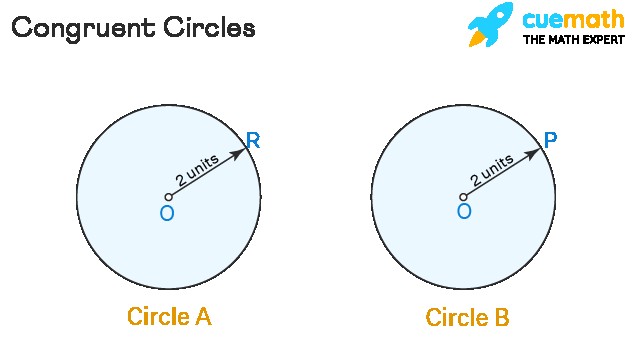
The term ‘congruent’ in geometry signifies that two figures are precisely the same in terms of their shape and size. This equivalence holds true even when the shapes are turned, flipped, or rotated. Consider two circles with identical radii; if you were to cut them out and place one on top of the other, they would perfectly overlap. This perfect overlap illustrates the concept of congruence. Since circle A is congruent to circle B, we can express this fact as follows: Circle A ≅ Circle B.
Alt Text: Two circles with equal radii, demonstrating congruent shapes.
2. Exploring Congruent Figures
Two figures are considered congruent if one can be placed precisely over the other, perfectly coinciding. The term ‘congruence’ describes the relationship between these identical figures. Geometrical figures that can be superimposed on one another are classified as congruent figures. This principle applies universally to figures such as triangles, quadrilaterals, and beyond. Additionally, line segments and angles are considered congruent when they possess equal measures.
Alt Text: Examples of congruent figures including triangles, squares, and other polygons.
3. Congruent vs. Similar Figures: Understanding the Difference
It’s crucial to differentiate between congruent and similar figures. Congruent figures possess not only the same shape but also identical side lengths and angles. Similar figures, on the other hand, share the same shape but may differ in size. In congruent figures, all corresponding sides and angles are equal. In similar figures, corresponding angles are equal, but the sides are proportional, not necessarily equal.
Alt Text: A comparison showing congruent figures with equal sides and angles versus similar figures with proportional sides and equal angles.
4. Diving Deep into Congruence of Triangles
Two triangles are deemed congruent if their corresponding sides are equal in length, their corresponding angles are of equal measure, and one can be superimposed exactly onto the other.
Alt Text: Two congruent triangles labeled ABC and PQR, highlighting corresponding equal sides and angles.
In the figure above, Δ ABC and Δ PQR are congruent triangles. This signifies that the corresponding angles and corresponding sides in both triangles are equivalent.
- Sides: AB = PQ, BC = QR, and AC = PR
- Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R
Therefore, Δ ABC ≅ Δ PQR
Several congruence theorems or triangle congruence criteria exist to prove the congruence of triangles:
- SSS (Side, Side, Side)
- SAS (Side, Angle, Side)
- ASA (Angle, Side, Angle)
- AAS (Angle, Angle, Side)
- RHS (Right angle-Hypotenuse-Side or the Hypotenuse Leg theorem)
5. Exploring Congruent Polygons Beyond Triangles
The concept of congruence extends beyond triangles to encompass all polygons. Two polygons are congruent if and only if all their corresponding sides and angles are equal. Consider two squares; if their side lengths are identical, they are congruent. Similarly, two regular pentagons are congruent if their side lengths are the same.
6. Practical Applications of Congruence
Congruence is not merely a theoretical concept; it has numerous practical applications in various fields:
- Construction: Ensuring that building components are congruent is crucial for structural integrity.
- Manufacturing: Mass production relies on creating congruent parts to ensure consistency and interchangeability.
- Engineering: Designing structures and machines requires precise congruence for proper functionality.
- Computer Graphics: Congruence is used in creating symmetrical designs and patterns.
- Architecture: From laying identical bricks to ensuring windows are the same size, congruent measurements are used constantly in this field.
- Art: Congruence can be used to create symmetrical designs, patterns, and tessellations in various forms of art, offering visual balance and harmony to the overall composition.
7. Congruence in Real Life: Everyday Examples
Congruence is all around us in everyday life:
- Identical coins: Coins of the same denomination produced at the same mint are congruent.
- Matching tiles: Tiles used in flooring or walls are designed to be congruent for a seamless appearance.
- Stackable chairs: Chairs designed to be stacked are congruent for efficient storage.
- Dominoes: Dominoes in a standard set are congruent rectangles with varying numbers of dots.
- Crystals: Certain crystals exhibit congruent faces and angles, reflecting their symmetrical atomic structure.
- Snowflakes: While each snowflake is unique, snowflakes often exhibit six-fold symmetry, with congruent patterns repeating across their structure.
8. Mastering Congruence: Tips and Tricks
Here are some helpful tips for understanding and working with congruence:
- Visualize superimposition: Imagine placing one figure on top of the other to check for congruence.
- Focus on corresponding parts: Ensure that all corresponding sides and angles are equal.
- Use congruence theorems: Apply the appropriate theorems (SSS, SAS, ASA, AAS, RHS) to prove triangle congruence.
- Pay attention to notation: Use the congruence symbol (≅) correctly.
- Practice problem-solving: Work through various examples to solidify your understanding.
9. Common Mistakes to Avoid When Working with Congruence
- Confusing congruence with similarity: Remember that congruent figures are identical in size and shape, while similar figures only share the same shape.
- Assuming congruence based on appearance: Always verify congruence by checking corresponding sides and angles.
- Misinterpreting congruence theorems: Ensure that you are applying the correct theorem based on the given information.
- Neglecting to check all corresponding parts: All corresponding sides and angles must be equal for congruence to hold true.
- Ignoring transformations: Keep in mind that congruent figures remain congruent even after transformations such as rotations, reflections, and translations.
10. Exploring Congruence Transformations: Preserving Shapes
Congruence transformations are operations that preserve the shape and size of a figure while changing its position or orientation. There are four main types of congruence transformations:
- Translation: Sliding a figure along a straight line without changing its orientation.
- Rotation: Turning a figure around a fixed point.
- Reflection: Flipping a figure over a line, creating a mirror image.
- Glide Reflection: A combination of a translation and a reflection.
11. The Importance of Congruence in Advanced Mathematics
Congruence forms the foundation for many advanced mathematical concepts:
- Geometry: Congruence is used in proofs, constructions, and geometric transformations.
- Trigonometry: Congruent triangles are used to define trigonometric ratios and solve problems involving angles and sides of triangles.
- Calculus: Congruence is used in understanding symmetry and transformations of functions.
- Linear Algebra: Congruent matrices have the same eigenvalues, which are important in analyzing linear transformations.
12. Congruence and Symmetry: A Harmonious Relationship
Symmetry is closely related to congruence. A figure is symmetrical if it can be divided into two or more congruent parts that are mirror images of each other or that can be rotated to coincide with each other.
There are different types of symmetry:
- Line Symmetry (Reflectional Symmetry): A figure has line symmetry if it can be reflected across a line to coincide with itself.
- Rotational Symmetry: A figure has rotational symmetry if it can be rotated around a point to coincide with itself.
- Point Symmetry (Inversional Symmetry): A figure has point symmetry if it can be rotated 180 degrees around a point to coincide with itself.
13. Common Notations and Symbols for Congruence
- The symbol for congruence is ≅. For example, Δ ABC ≅ Δ XYZ means that triangle ABC is congruent to triangle XYZ.
- Tick marks are used to indicate congruent sides in figures.
- Arc marks are used to indicate congruent angles in figures.
- Corresponding vertices are listed in the same order when stating congruence. For example, if Δ ABC ≅ Δ XYZ, then A corresponds to X, B corresponds to Y, and C corresponds to Z.
14. The Historical Development of Congruence
The concept of congruence has been used implicitly throughout the history of mathematics. The ancient Greeks, including Euclid, used congruence in their geometric constructions and proofs. However, a formal definition of congruence and the development of congruence theorems came later, during the 19th century.
15. Advanced Congruence Theorems and Concepts
Beyond the basic congruence theorems (SSS, SAS, ASA, AAS, RHS), there are more advanced concepts and theorems related to congruence:
- CPCTC (Corresponding Parts of Congruent Triangles are Congruent): This theorem states that if two triangles are congruent, then all their corresponding parts (sides and angles) are congruent.
- The Hinge Theorem (SAS Inequality): This theorem states that if two sides of one triangle are congruent to two sides of another triangle, but the included angle of the first triangle is larger than the included angle of the second triangle, then the third side of the first triangle is longer than the third side of the second triangle.
- The Converse of the Hinge Theorem (SSS Inequality): This theorem states that if two sides of one triangle are congruent to two sides of another triangle, but the third side of the first triangle is longer than the third side of the second triangle, then the included angle of the first triangle is larger than the included angle of the second triangle.
16. The Role of Congruence in Geometric Proofs
Congruence plays a crucial role in geometric proofs. By proving that two figures are congruent, you can establish that their corresponding parts are equal, which can then be used to prove other statements. Congruence theorems are essential tools for constructing logical arguments and demonstrating geometric relationships.
17. Exploring Tessellations with Congruent Shapes
A tessellation is a pattern of congruent shapes that covers a plane without gaps or overlaps. Tessellations can be created using regular polygons (equilateral and equiangular) such as squares, equilateral triangles, and regular hexagons. They can also be created using irregular polygons and other shapes.
18. Congruence in Three-Dimensional Geometry
The concept of congruence extends to three-dimensional geometry as well. Two three-dimensional figures are congruent if they have the same shape and size. For example, two cubes with the same side length are congruent. Similarly, two spheres with the same radius are congruent.
19. Further Exploration: Resources for Learning More About Congruence
To deepen your understanding of congruence, consider exploring these resources:
- Textbooks: Geometry textbooks provide comprehensive coverage of congruence and related concepts.
- Online Courses: Platforms like Coursera, Khan Academy, and Udemy offer courses on geometry that cover congruence.
- Websites: Websites like MathWorld and Wolfram Alpha provide detailed explanations and examples of congruence.
- Interactive Tools: GeoGebra and other interactive geometry software allow you to explore congruence visually.
20. Congruence in Art and Design: Creating Harmony
Congruence plays a significant role in art and design, contributing to visual harmony and balance. Artists and designers use congruence to create patterns, symmetries, and repeating motifs. Congruent elements can create a sense of order and predictability, while variations in congruence can add visual interest and complexity.
21. Congruence and the Golden Ratio: Perfect Proportions
The golden ratio, approximately 1.618, is a mathematical constant that appears frequently in nature and is often used in art and design to create aesthetically pleasing proportions. Congruence can be used in conjunction with the golden ratio to create harmonious compositions. For example, a rectangle with sides in the golden ratio can be divided into a square and another rectangle that is similar to the original rectangle. This process can be repeated infinitely, creating a self-similar pattern.
22. Congruence in Nature: Patterns of Repetition
Nature is full of examples of congruence, from the repeating patterns in snowflakes to the symmetrical arrangement of petals in a flower. These patterns often arise from underlying mathematical principles and contribute to the beauty and complexity of the natural world.
23. Congruence in Music: Repeating Themes and Motifs
In music, congruence can be seen in the repetition of themes, motifs, and rhythmic patterns. These repeating elements create a sense of unity and coherence in a musical composition. Variations in these elements can add interest and complexity, while still maintaining a sense of overall structure.
24. Common Congruence Problems and Solutions
Let’s explore some common problems related to congruence and their solutions:
Problem 1: Given two triangles, Δ ABC and Δ DEF, with AB = DE, BC = EF, and CA = FD, prove that Δ ABC ≅ Δ DEF.
Solution: By the SSS (Side, Side, Side) congruence theorem, if all three sides of one triangle are congruent to the corresponding sides of another triangle, then the triangles are congruent. Therefore, Δ ABC ≅ Δ DEF.
Problem 2: Given two triangles, Δ PQR and Δ XYZ, with PQ = XY, ∠P = ∠X, and ∠Q = ∠Y, prove that Δ PQR ≅ Δ XYZ.
Solution: By the ASA (Angle, Side, Angle) congruence theorem, if two angles and the included side of one triangle are congruent to the corresponding two angles and included side of another triangle, then the triangles are congruent. Therefore, Δ PQR ≅ Δ XYZ.
Problem 3: Given two right triangles, Δ LMN and Δ OPQ, with ∠M = ∠P = 90°, LN = OQ, and LM = OP, prove that Δ LMN ≅ Δ OPQ.
Solution: By the RHS (Right angle-Hypotenuse-Side) congruence theorem, if the hypotenuse and one side of one right triangle are congruent to the hypotenuse and the corresponding side of another right triangle, then the triangles are congruent. Therefore, Δ LMN ≅ Δ OPQ.
25. Real-World Congruence Examples
Congruence is an important concept with many real-world applications. Here are some real-world examples of congruence:
- Assembly Lines: In manufacturing, parts are often made to be congruent so that they can be easily interchanged.
- Construction: Builders use congruent materials and measurements to ensure that structures are stable and safe.
- Design: Designers use congruent shapes and patterns to create visually appealing and functional products.
26. Visualizing Congruence with Interactive Tools
Interactive geometry software like GeoGebra can be used to visualize and explore congruence. These tools allow you to create and manipulate geometric figures, measure their sides and angles, and test for congruence.
27. The Cognitive Benefits of Understanding Congruence
Understanding congruence can enhance cognitive skills such as:
- Spatial Reasoning: Congruence helps develop spatial reasoning skills, which are important for problem-solving and decision-making in various fields.
- Logical Thinking: Proving congruence requires logical thinking and deductive reasoning skills.
- Visual Perception: Congruence enhances visual perception skills, allowing you to identify and analyze geometric patterns.
28. How to Explain Congruence to a Child
Explaining congruence to a child can be done using simple and relatable examples:
- Cookies: “Imagine you have two cookies that are exactly the same shape and size. Those cookies are congruent!”
- Building Blocks: “If you have two building blocks that are the same shape and size, you can stack them perfectly on top of each other. That means they are congruent.”
- Hands: “Your hands are almost congruent. They are the same shape, but they are mirror images of each other.”
29. Congruence in Computer Graphics and Animation
In computer graphics and animation, congruence is used to create realistic and visually appealing images. Congruent objects can be easily duplicated and manipulated, saving time and resources.
30. Congruence and Cryptography: Secure Communication
Congruence can be used in cryptography to create secure communication systems. For example, congruent keys can be used to encrypt and decrypt messages, ensuring that only authorized users can read them.
Still have questions about congruence? Head over to WHAT.EDU.VN! Our community of experts is ready to provide you with personalized guidance and answer any questions you may have.
We understand that finding answers can sometimes feel like navigating a maze. You might not know who to ask, or where to find reliable information. That’s why WHAT.EDU.VN is here. We offer a free platform where you can ask any question and receive prompt, accurate answers.
Don’t let your curiosity wait! Visit WHAT.EDU.VN today and experience the ease of getting your questions answered.
Contact us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: what.edu.vn