Cosecant: Are you curious about the cosecant function and its significance in trigonometry? WHAT.EDU.VN offers a clear explanation, providing the cosecant definition, formula, and applications. Discover the cosecant, its properties, and how it relates to other trigonometric functions. Need free answers?
Table of Contents
- Delving into the Cosecant Function
- The Cosecant Formula Unveiled
- Exploring the Domain and Range of Cosecant
- Visualizing the Cosecant Graph
- Essential Cosecant Identities
- Key Properties of the Cosecant Function
- Common Cosecant Values
- Cosecant Function in Real-World Applications
- Practical Cosecant Examples
- Frequently Asked Questions About Cosecant
1. Delving into the Cosecant Function
The cosecant function, often abbreviated as csc(x), stands as a fundamental concept within trigonometry. It’s one of the six primary trigonometric functions, alongside sine, cosine, tangent, cotangent, and secant.
But What Is Cosecant? In essence, the cosecant is the reciprocal of the sine function. This means that csc(x) = 1 / sin(x). In a right-angled triangle, the cosecant of an angle is defined as the ratio of the length of the hypotenuse to the length of the side opposite that angle. Understanding the cosecant function unlocks a deeper understanding of trigonometric relationships and their applications in various fields.
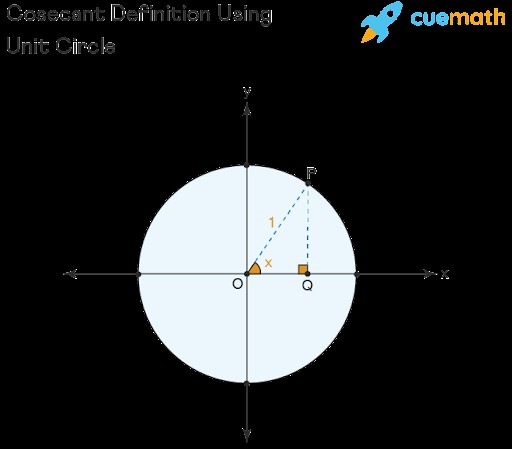
Understanding the cosecant function in relation to the unit circle
Let’s consider a unit circle, a circle with a radius of 1 unit, centered at the origin of a coordinate plane. If we draw a line from the origin to a point P on the circumference of the circle, forming an angle x with the positive x-axis, then the sine of x is represented by the y-coordinate of point P. Consequently, the cosecant of x is the reciprocal of that y-coordinate, or 1 divided by the y-coordinate.
2. The Cosecant Formula Unveiled
The cosecant formula is a direct consequence of its definition as the reciprocal of the sine function. As previously stated, this relationship is mathematically expressed as:
csc(x) = 1 / sin(x)
This formula is the cornerstone of calculating the cosecant of any angle, provided you know the sine of that angle. It also highlights the inverse relationship between these two trigonometric functions.
Another perspective on the cosecant formula comes from considering a right-angled triangle. In this context, the cosecant of an angle (let’s call it θ) is defined as the ratio of the length of the hypotenuse to the length of the side opposite to the angle:
csc(θ) = Hypotenuse / Opposite
The cosecant function and its relationship to the sides of a right-angled triangle
This formula is particularly useful when dealing with problems involving triangles and geometric calculations.
3. Exploring the Domain and Range of Cosecant
The domain and range of a function define the set of possible input values (domain) and the set of possible output values (range). For the cosecant function, these are determined by its relationship to the sine function.
Domain of Cosecant
Since csc(x) = 1 / sin(x), the cosecant function is undefined wherever the sine function is equal to zero. The sine function equals zero at all integer multiples of π (i.e., 0, π, 2π, -π, -2π, and so on). Therefore, the domain of the cosecant function is all real numbers except for these values. Mathematically, this can be expressed as:
Domain of csc(x) = {x ∈ ℝ | x ≠ nπ, where n is an integer}
This means that you can input any real number into the cosecant function, as long as it’s not an integer multiple of pi.
Range of Cosecant
The range of the cosecant function is also influenced by its reciprocal relationship with the sine function. The sine function has a range of [-1, 1], meaning its output values are always between -1 and 1, inclusive.
Because the cosecant is the reciprocal of the sine, its range consists of all real numbers greater than or equal to 1, and all real numbers less than or equal to -1. In interval notation, this is expressed as:
Range of csc(x) = (-∞, -1] ∪ [1, ∞)
This means that the output of the cosecant function will never fall between -1 and 1. It will always be either greater than or equal to 1, or less than or equal to -1.
4. Visualizing the Cosecant Graph
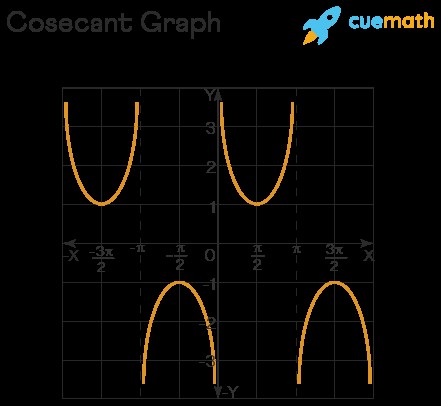
The cosecant graph provides a visual representation of the function’s behavior. It illustrates the domain, range, periodicity, and asymptotes of the cosecant function.
A visual representation of the cosecant graph, highlighting its key features
Key features of the cosecant graph:
- Vertical Asymptotes: As discussed earlier, the cosecant function is undefined at integer multiples of π. This results in vertical asymptotes at these points on the graph. As the x-value approaches these asymptotes, the value of csc(x) approaches either positive or negative infinity.
- Periodicity: The cosecant function is periodic with a period of 2π. This means that the graph repeats itself every 2π units along the x-axis.
- Shape: The graph consists of a series of U-shaped curves that alternate between opening upwards and downwards. These curves approach the vertical asymptotes but never intersect them.
- Range: As mentioned before, the range of the cosecant function is (-∞, -1] ∪ [1, ∞). This is reflected in the graph, as the curves never fall between the y-values of -1 and 1.
5. Essential Cosecant Identities
Trigonometric identities are equations that are true for all values of the variables involved. Cosecant identities are particularly useful for simplifying expressions, solving equations, and proving other trigonometric relationships. Here are some essential cosecant identities:
-
Reciprocal Identity: csc(x) = 1 / sin(x)
-
Pythagorean Identity: 1 + cot²(x) = csc²(x)
- This identity is derived from the fundamental Pythagorean identity sin²(x) + cos²(x) = 1. By dividing both sides of this equation by sin²(x), we obtain the cosecant form.
-
Cofunction Identities:
-
csc(π/2 – x) = sec(x)
-
sec(π/2 – x) = csc(x)
-
These identities relate the cosecant function to the secant function.
-
-
Odd Function Identity: csc(-x) = -csc(x)
- This identity indicates that the cosecant function is an odd function, meaning it is symmetrical about the origin.
6. Key Properties of the Cosecant Function
Understanding the properties of the cosecant function is crucial for working with it effectively. Here are some key properties:
- Periodicity: The cosecant function is periodic with a period of 2π. This means that csc(x + 2π) = csc(x) for all x in the domain of the function.
- Odd Function: The cosecant function is an odd function, meaning csc(-x) = -csc(x). This implies that the graph of the cosecant function is symmetrical about the origin.
- Vertical Asymptotes: The cosecant function has vertical asymptotes at x = nπ, where n is an integer. This is because the sine function is equal to zero at these points, and the cosecant is the reciprocal of the sine.
- Range: The range of the cosecant function is (-∞, -1] ∪ [1, ∞). This means that the value of csc(x) is always greater than or equal to 1, or less than or equal to -1.
- No x-intercepts: The cosecant graph does not intersect the x-axis. This is because the cosecant function is never equal to zero.
7. Common Cosecant Values
Memorizing the cosecant values for certain common angles can be helpful for quick calculations and problem-solving. Here’s a table of cosecant values for some frequently used angles:
| Angle (x) | Cosecant (csc x) |
|---|---|
| 0 | Undefined |
| π/6 (30°) | 2 |
| π/4 (45°) | √2 |
| π/3 (60°) | 2/√3 |
| π/2 (90°) | 1 |
| π (180°) | Undefined |
| 3π/2 (270°) | -1 |
| 2π (360°) | Undefined |

These values can be derived from the corresponding sine values, as csc(x) = 1 / sin(x).
8. Cosecant Function in Real-World Applications
While the cosecant function may seem abstract, it has practical applications in various fields, including:
- Navigation: Calculating angles and distances in surveying and marine navigation.
- Engineering: Designing structures, analyzing forces, and working with oscillatory motion.
- Physics: Modeling wave phenomena, such as light and sound waves.
- Astronomy: Determining the positions and distances of celestial objects.
In many of these applications, the cosecant function is used in conjunction with other trigonometric functions to solve complex problems involving angles, triangles, and periodic phenomena.
9. Practical Cosecant Examples
Let’s work through a few examples to solidify your understanding of the cosecant function:
Example 1: Finding the Cosecant from Sine
If sin(x) = 3/5, find csc(x).
Solution:
Using the reciprocal identity, we know that csc(x) = 1 / sin(x).
Therefore, csc(x) = 1 / (3/5) = 5/3.
Example 2: Using the Pythagorean Identity
If cot(x) = 4/3 and x is in the first quadrant, find csc(x).
Solution:
Using the Pythagorean identity, 1 + cot²(x) = csc²(x).
Substituting the given value, we have 1 + (4/3)² = csc²(x).
Simplifying, 1 + 16/9 = csc²(x).
Therefore, csc²(x) = 25/9.
Taking the square root of both sides, we get csc(x) = ±5/3.
Since x is in the first quadrant, csc(x) is positive. Therefore, csc(x) = 5/3.
Example 3: Solving a Right Triangle Problem
In a right triangle, the hypotenuse is 13 cm and the side opposite angle θ is 5 cm. Find csc(θ).
Solution:
Using the definition of cosecant in a right triangle, csc(θ) = Hypotenuse / Opposite.
Therefore, csc(θ) = 13 cm / 5 cm = 2.6.
10. Frequently Asked Questions About Cosecant
What is the cosecant function?
The cosecant function (csc) is a trigonometric function that is the reciprocal of the sine function. In a right-angled triangle, it is the ratio of the hypotenuse to the length of the opposite side.
What is the formula for cosecant?
The formula for cosecant is csc(x) = 1 / sin(x) or csc(θ) = Hypotenuse / Opposite.
What is the domain of the cosecant function?
The domain of the cosecant function is all real numbers except for integer multiples of π, i.e., x ≠ nπ, where n is an integer.
What is the range of the cosecant function?
The range of the cosecant function is all real numbers greater than or equal to 1, or less than or equal to -1, i.e., (-∞, -1] ∪ [1, ∞).
Is the cosecant function even or odd?
The cosecant function is an odd function, meaning csc(-x) = -csc(x).
What is the period of the cosecant function?
The period of the cosecant function is 2π.
Where can I get more help with trigonometry?
WHAT.EDU.VN provides a platform for asking any question and receiving free answers. If you need help with the cosecant function or any other topic in trigonometry, simply ask your question on our website. Our community of experts is ready to provide clear, concise, and helpful explanations.
Do you have more questions about the cosecant function or other math topics? Don’t hesitate to ask!
Contact us at:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: what.edu.vn
We are here to help you learn and succeed!
