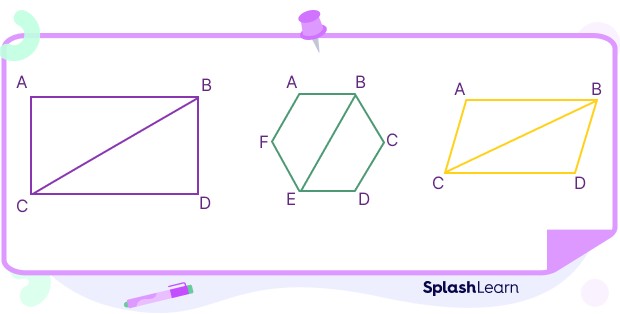
Are you struggling to grasp the concept of What Is Diagonal? At WHAT.EDU.VN, we simplify geometry for everyone, providing clear explanations and examples. Discover the definition of a diagonal, explore its formula, and see real-world applications.
1. Understanding What Is Diagonal: A Comprehensive Guide
A diagonal is a line segment that connects two non-adjacent vertices (corners) of a polygon or a polyhedron. In simpler terms, it’s a line that goes from one corner of a shape to another, but it’s not one of the sides. Diagonals are fundamental in geometry and have various applications in mathematics, engineering, and design. Let’s explore this concept further.
1.1. What is Diagonal in Polygons?
In polygons, a diagonal is a line segment joining two vertices that are not already connected by a side. For example, in a square, a diagonal connects opposite corners.
Alt Text: A square with a red diagonal line connecting opposite corners, illustrating what is diagonal in a polygon.
1.2. What is Diagonal in Solid Shapes?
In solid or three-dimensional shapes, diagonals can be classified into two types: face diagonals and space diagonals. Face diagonals lie on one of the faces of the solid, while space diagonals pass through the interior of the solid.
Alt Text: Illustration of diagonals in 3D shapes including a cube and a cuboid, showing face and space diagonals.
1.3. Historical Perspective on Diagonals
The term “diagonal” has its roots in ancient Greek. The word diagonios meant “from angle to angle.” Ancient mathematicians like Euclid and Strabo used the term to describe lines connecting vertices in shapes like rhombuses and cuboids. The Latin term diagonus, meaning “slanting line,” further solidified its usage.
2. Delving into Diagonal Formulas and Calculations
Understanding how to calculate the number and length of diagonals is crucial. Here, we explore the formulas and methods used for different shapes.
2.1. Diagonal Formula for Polygons
The number of diagonals in a polygon with n vertices can be calculated using the formula:
Number of diagonals = $frac{n(n-3)}{2}$
Alt Text: Formula for calculating the number of diagonals in a polygon with n vertices.
For example, a hexagon (6 sides) has $frac{6(6-3)}{2}$ = 9 diagonals.
2.2. Length of Diagonal in a Square
The length of the diagonal (d) of a square with side a can be found using the Pythagorean theorem:
$d = asqrt{2}$
So, if a square has sides of 5 cm, the diagonal is $5sqrt{2}$ cm.
2.3. Length of Diagonal in a Rectangle
For a rectangle with length (l) and breadth (b), the diagonal (d) is:
$d = sqrt{l^{2} + b^{2}}$
Alt Text: Rectangle with labeled length l, breadth b, and diagonal d, illustrating the formula to calculate diagonal length.
For example, if a rectangle is 8 cm long and 6 cm wide, the diagonal is $sqrt{8^{2} + 6^{2}}$ = 10 cm.
3. Practical Examples and Solved Problems
To solidify your understanding, let’s walk through some solved examples involving diagonals.
3.1. Example 1: Number of Diagonals in a Decagon
Question: How many diagonals does a decagon (10 sides) have?
Solution: Using the formula $frac{n(n-3)}{2}$, we get:
$frac{10(10-3)}{2} = frac{10 times 7}{2} = 35$
A decagon has 35 diagonals.
3.2. Example 2: Diagonal Length of a Square
Question: What is the length of the diagonal of a square with a side of 7 cm?
Solution: Using the formula $d = asqrt{2}$, we get:
$d = 7sqrt{2}$ cm
3.3. Example 3: Diagonal Length of a Rectangle
Question: A rectangle has a length of 12 cm and a width of 5 cm. What is the length of its diagonal?
Solution: Using the formula $d = sqrt{l^{2} + b^{2}}$, we get:
$d = sqrt{12^{2} + 5^{2}} = sqrt{144 + 25} = sqrt{169} = 13$ cm
4. Common Questions and Answers About Diagonals
4.1. What Polygons Have Diagonals That Bisect Each Other?
In some quadrilaterals such as rectangles, squares, parallelograms, and rhombuses, the diagonals bisect each other, meaning they cut each other into two equal parts.
4.2. Why Doesn’t a Triangle Have a Diagonal?
A diagonal is a line connecting non-adjacent vertices. A triangle is the simplest polygon, and every vertex is adjacent to every other vertex. Therefore, it is not possible to draw a diagonal in a triangle.
4.3. Which Polygon Has the Same Number of Sides and Diagonals?
A pentagon has five sides and five diagonals. Using the formula, $frac{5(5-3)}{2} = 5$.
5. Practice Problems to Test Your Knowledge
Test your understanding with these practice problems.
5.1. Problem 1
How many diagonals does an octagon (8 sides) have?
5.2. Problem 2
The side of a square is 9 cm. What is the length of its diagonal?
5.3. Problem 3
A rectangle has a length of 15 cm and a breadth of 8 cm. Find the length of its diagonal.
6. Real-World Applications of Diagonals
Diagonals are not just theoretical concepts. They are used in various practical applications.
6.1. Engineering and Architecture
In structural engineering, diagonals are used to provide stability to structures. For example, diagonal beams in bridges and buildings help distribute weight and resist deformation.
6.2. Computer Graphics
Diagonals are used in computer graphics to calculate distances and create geometric shapes. They are also used in image processing and pattern recognition.
6.3. Sports and Games
In sports like basketball and soccer, understanding diagonals can help players make better passes and strategic moves. In board games like chess, the diagonal movement of pieces is crucial for gameplay.
7. Diagonals in Different Geometric Shapes
7.1. Diagonals in Quadrilaterals
Quadrilaterals, with their four sides and four vertices, present interesting diagonal properties. Depending on the type of quadrilateral, the diagonals may or may not bisect each other, be equal in length, or intersect at right angles.
- Square: Diagonals are equal in length, bisect each other at right angles.
- Rectangle: Diagonals are equal in length and bisect each other.
- Parallelogram: Diagonals bisect each other but are not equal in length.
- Rhombus: Diagonals bisect each other at right angles but are not equal in length.
- Trapezoid: Diagonals do not necessarily bisect each other nor are they equal, unless it’s an isosceles trapezoid.
7.2. Diagonals in Regular Polygons
Regular polygons, with their equal sides and equal angles, have diagonals that exhibit symmetry and predictability. The number of diagonals increases significantly as the number of sides increases.
- Pentagon: 5 diagonals
- Hexagon: 9 diagonals
- Heptagon: 14 diagonals
- Octagon: 20 diagonals
7.3. Diagonals in Three-Dimensional Shapes
In three-dimensional shapes, diagonals can be categorized into face diagonals (lying on the faces) and space diagonals (passing through the interior). Understanding these diagonals is crucial in fields like architecture and engineering.
- Cube: Has face diagonals on each of its six faces and space diagonals that connect opposite vertices through the center of the cube.
- Cuboid: Similar to a cube, but with varying lengths, widths, and heights, affecting the lengths of the diagonals.
8. Advanced Concepts Related to Diagonals
8.1. Using Diagonals to Find Area
Diagonals can be used to calculate the area of certain polygons. For example, the area of a rhombus can be calculated as half the product of its diagonals:
Area = $frac{1}{2} times d_1 times d_2$
where $d_1$ and $d_2$ are the lengths of the diagonals.
8.2. Diagonals and Symmetry
Diagonals often reveal the symmetry of a polygon. In regular polygons, diagonals create symmetrical patterns that can be mathematically analyzed. This is particularly useful in fields like crystallography and material science.
8.3. Diagonals in Graph Theory
In graph theory, the concept of diagonals extends to the connections between vertices in a graph. Understanding these connections is vital in network analysis, computer science, and operations research.
9. Visualizing Diagonals
9.1. Interactive Tools for Exploring Diagonals
Online interactive tools like GeoGebra and Desmos allow users to visualize diagonals in various polygons and explore their properties. These tools are invaluable for both students and educators.
9.2. Diagrams and Illustrations
Clear diagrams and illustrations are essential for understanding diagonals. Visual aids help to clarify the concept and make it easier to remember the formulas and properties.
9.3. Real-Life Examples
Looking for diagonals in real-life objects can reinforce understanding. Examples include the crossbars in gates, the support structures in bridges, and the patterns in architectural designs.
10. Why Understanding Diagonals is Important
10.1. Problem-Solving Skills
Understanding diagonals enhances problem-solving skills, particularly in geometry and spatial reasoning. These skills are transferable to various fields, including engineering, architecture, and computer science.
10.2. Mathematical Foundations
Diagonals provide a foundation for more advanced mathematical concepts. They are essential in understanding trigonometry, calculus, and linear algebra.
10.3. Practical Applications
From structural engineering to computer graphics, diagonals have numerous practical applications. Understanding diagonals enables you to apply mathematical principles to real-world problems.
11. Common Mistakes to Avoid When Working with Diagonals
11.1. Confusing Sides with Diagonals
One common mistake is confusing the sides of a polygon with its diagonals. Remember that diagonals connect non-adjacent vertices, while sides connect adjacent vertices.
11.2. Incorrectly Applying Formulas
Another mistake is applying the diagonal formula incorrectly. Ensure you are using the correct formula for the specific shape you are working with.
11.3. Misunderstanding Three-Dimensional Diagonals
Three-dimensional diagonals can be tricky. Differentiate between face diagonals (which lie on the surface) and space diagonals (which pass through the interior).
12. Tips and Tricks for Mastering Diagonals
12.1. Practice Regularly
Consistent practice is key to mastering diagonals. Work through a variety of problems and examples to reinforce your understanding.
12.2. Use Visual Aids
Visual aids like diagrams and interactive tools can help you visualize diagonals and understand their properties.
12.3. Seek Help When Needed
Don’t hesitate to seek help from teachers, tutors, or online resources if you are struggling with diagonals. At WHAT.EDU.VN, we are here to help.
13. Diagonals in Art and Design
13.1. Composition and Balance
In art and design, diagonals are often used to create a sense of movement and dynamism. They can add tension or balance to a composition.
13.2. Perspective and Depth
Diagonals play a crucial role in creating perspective and depth in visual art. They guide the viewer’s eye and create a sense of space.
13.3. Geometric Patterns
Diagonals are used to create intricate geometric patterns in various art forms, from mosaics to textile designs.
14. Diagonals in Games and Puzzles
14.1. Chess and Checkers
In chess and checkers, diagonal moves are fundamental to gameplay. They allow pieces to control key squares and launch attacks.
14.2. Sudoku and Crosswords
Diagonals can add an extra layer of complexity to puzzles like Sudoku and crosswords. They require players to think strategically and make connections between different parts of the puzzle.
14.3. Video Games
Diagonals are essential in video games for character movement, camera angles, and level design. They create a more immersive and dynamic gaming experience.
15. The Role of Diagonals in Tessellations
15.1. Creating Repeating Patterns
Tessellations are repeating patterns made up of geometric shapes. Diagonals can be used to create tessellations with intricate designs and symmetries.
15.2. Mathematical Properties
The mathematical properties of diagonals determine which shapes can be used to create tessellations. Understanding these properties is crucial in fields like architecture and design.
15.3. Examples in Nature and Architecture
Tessellations can be found in nature, from honeycombs to crystal structures. They are also commonly used in architecture, from tiled floors to decorative facades.
16. Diagonals in Surveying and Mapping
16.1. Measuring Distances
In surveying and mapping, diagonals are used to measure distances and create accurate maps. They provide a direct line of sight between two points, allowing for precise measurements.
16.2. Creating Triangulation Networks
Diagonals are used to create triangulation networks, which are essential for accurate surveying and mapping. These networks provide a framework for measuring distances and elevations.
16.3. Applications in Construction and Land Management
The principles of surveying and mapping are used in construction and land management to ensure accurate measurements and proper alignment of structures.
17. Diagonals in Computer-Aided Design (CAD)
17.1. Creating Geometric Models
In CAD, diagonals are used to create precise geometric models. They define the shapes and dimensions of objects, allowing for accurate design and manufacturing.
17.2. Analyzing Structural Integrity
Diagonals are used to analyze the structural integrity of designs. They help engineers identify potential weaknesses and ensure that structures are strong and stable.
17.3. Applications in Engineering and Architecture
CAD is used in a wide range of engineering and architectural applications, from designing bridges and buildings to creating consumer products.
18. Diagonals in Robotics
18.1. Navigation and Path Planning
In robotics, diagonals are used for navigation and path planning. They help robots find the shortest and most efficient routes between two points.
18.2. Object Recognition
Diagonals are used in object recognition to identify and classify objects based on their geometric properties. This is essential for tasks like autonomous driving and industrial automation.
18.3. Applications in Manufacturing and Exploration
Robotics is used in a variety of manufacturing and exploration applications, from assembling products on a factory floor to exploring distant planets.
19. The Future of Diagonals in Mathematics and Technology
19.1. Advancements in Geometric Research
Ongoing research in geometry continues to explore the properties and applications of diagonals. These advancements may lead to new discoveries and innovations in mathematics and technology.
19.2. Emerging Technologies
Emerging technologies like artificial intelligence and virtual reality are creating new opportunities for the use of diagonals. These technologies can enhance our understanding of geometric concepts and enable new applications.
19.3. Educational Tools and Resources
The development of new educational tools and resources is making it easier for students to learn about diagonals. These tools can help students visualize geometric concepts and develop problem-solving skills.
20. Resources for Further Learning
20.1. Online Courses and Tutorials
Numerous online courses and tutorials are available for learning about diagonals. These resources provide in-depth explanations and examples that can help you master the concept.
20.2. Textbooks and Reference Materials
Textbooks and reference materials offer a comprehensive overview of diagonals and their applications. These resources are valuable for students and professionals alike.
20.3. Websites and Forums
Websites and forums dedicated to mathematics and geometry provide a platform for discussing diagonals and related topics. These resources can help you connect with other learners and experts in the field.
21. Test Your Knowledge: Quiz on Diagonals
21.1. Question 1:
How many diagonals does a polygon with 7 sides have?
A) 14
B) 7
C) 10
D) 21
21.2. Question 2:
What is the length of the diagonal of a square with a side length of 4 cm?
A) 4 cm
B) $4sqrt{2}$ cm
C) 8 cm
D) $8sqrt{2}$ cm
21.3. Question 3:
What quadrilateral has diagonals that bisect each other at right angles?
A) Rectangle
B) Parallelogram
C) Rhombus
D) Trapezoid
22. Conclusion: Mastering the Concept of Diagonals
Understanding what is diagonal is essential for anyone studying geometry or related fields. From calculating the number of diagonals in a polygon to applying diagonals in engineering and design, this concept has numerous practical applications. By mastering diagonals, you can enhance your problem-solving skills and gain a deeper appreciation for mathematics.
At WHAT.EDU.VN, we are committed to providing clear, concise, and accurate information to help you succeed. If you have any questions or need further assistance, don’t hesitate to reach out.
Are you still curious about geometrical concepts? Do you need help with a tricky math problem? Don’t worry! At WHAT.EDU.VN, we offer a free question-and-answer service. Simply post your question, and our community of experts will provide you with a detailed and accurate answer.
We’re here to help you succeed in your academic pursuits. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or via Whatsapp at +1 (206) 555-7890. Visit our website at WHAT.EDU.VN to ask your questions and explore more learning resources. Let WHAT.EDU.VN be your guide to mastering geometry and beyond. Let us help you clarify those definitions and formulas today, and remember, no question is too difficult for our team of experts. Benefit from our community-driven knowledge base today. Master shape properties with what.edu.vn and our dedicated team committed to knowledge sharing and growth.