Functions are fundamental tools in mathematics, acting like machines that take an input and produce a unique output. Understanding the domain and range is crucial for grasping how functions work and their limitations. Just like a vending machine accepts specific coins and dispenses certain items, a function operates on a defined set of inputs (domain) to generate a set of possible outputs (range).
Let’s explore the concepts of domain and range in detail, learning how to identify them for different types of functions and interpret them from graphs.
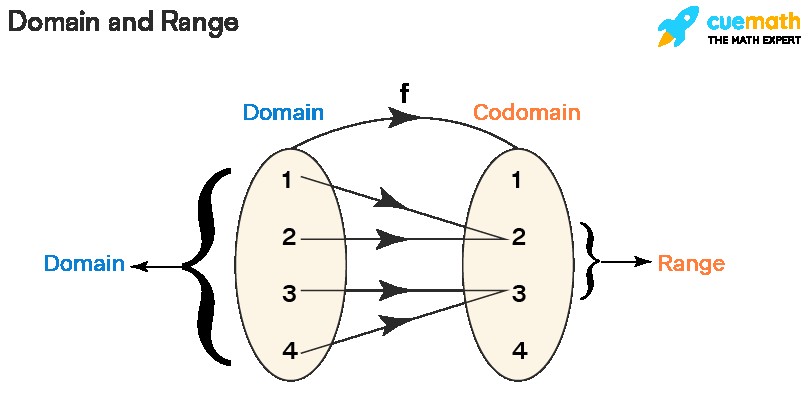
Understanding Domain and Range
In mathematics, particularly in the study of relations and functions, domain and range are essential concepts. For a relation, which is simply a set of ordered pairs, the domain is the set of all first elements (x-coordinates), and the range is the set of all second elements (y-coordinates).
Consider this relation R = {(1, 2), (2, 2), (3, 3), (4, 3)}.
- Domain = {1, 2, 3, 4} (set of all x-values)
- Range = {2, 3} (set of all y-values)
This can be visualized as:
The concept of domain and range becomes even more significant when we talk about functions, which are special types of relations.
Defining Domain of a Function
The domain of a function is formally defined as the complete set of possible input values, or independent variable values, for which the function is defined. In simpler terms, it’s all the ‘x’ values that you are allowed to plug into the function without causing it to be undefined.
Imagine a function as a process, like our earlier vending machine example. The domain is like the types of currency the machine accepts – if it only takes quarters and dollar bills, then pennies are not in the domain of acceptable inputs.
For a function denoted as f(x), the domain encompasses all possible values of ‘x’ that produce a valid output. For instance, if we have a function f(x) = 2x, and we consider the domain to be natural numbers (N), then inputs are {1, 2, 3, 4,…}. However, if no specific domain is mentioned, we generally consider the domain to be all real numbers (ℝ) for which the function is mathematically defined. For f(x) = 2x without restrictions, the domain is all real numbers, expressed in interval notation as (-∞, ∞).
Here’s a table summarizing rules for finding the domain for common function types:
| Function Type | Rule for Domain | Example | Domain |
|---|---|---|---|
| Polynomial Function | All real numbers | f(x) = x² + 3x – 2 | ℝ or (-∞, ∞) |
| Rational Function | Denominator cannot be zero | g(x) = 1/(x – 2) | ℝ except x = 2 or (-∞, 2) ∪ (2, ∞) |
| Square Root Function | Expression under the root must be non-negative (≥ 0) | h(x) = √(x + 3) | x ≥ -3 or [-3, ∞) |
| Logarithmic Function | Argument of logarithm must be positive (> 0) | k(x) = ln(x) | x > 0 or (0, ∞) |
How to Determine the Domain of a Function?
To find the domain, you need to identify any restrictions on the input values based on the function’s definition. Let’s look at examples:
Example 1: Finding the Domain of a Square Root Function
For f(x) = √(x + 3), the expression under the square root (x + 3) must be greater than or equal to zero.
x + 3 ≥ 0
x ≥ -3
Therefore, the domain of f(x) is [-3, ∞).
Example 2: Finding the Domain of a Rational Function
For g(x) = (2x + 1) / (x – 2), the denominator (x – 2) cannot be zero.
x – 2 ≠ 0
x ≠ 2
Thus, the domain of g(x) is all real numbers except 2, which is written in interval notation as (-∞, 2) ∪ (2, ∞).
Exploring Range of a Function
The range of a function is the set of all possible output values, or dependent variable values, that the function can produce. It’s the set of all ‘y’ values that result from plugging in all possible ‘x’ values from the domain.
Continuing with our function-as-a-machine analogy, the range is like the selection of soda flavors the vending machine offers. No matter how much money you insert (within the domain), you will only get a soda flavor that’s within the machine’s range of outputs, not a cheeseburger.
For a function f: A → B, where A is the domain and B is the codomain, the range is a subset of the codomain B and consists of all images of elements in A. For f(x) = 2x with domain A (natural numbers) and codomain B (natural numbers), the range is the set of even natural numbers. Elements of the domain are pre-images, and corresponding elements in the range are images.
Rules for Determining the Range of a Function
Finding the range can sometimes be more complex than finding the domain. Graphing the function is often the most visual and effective method to determine the range by observing the y-values the graph covers. However, here are general rules for common function types:
| Function Type | Rule for Range | Example | Range |
|---|---|---|---|
| Linear Function | All real numbers | f(x) = 2x + 1 | ℝ or (-∞, ∞) |
| Quadratic Function | Depends on the vertex form y = a(x – h)² + k: y ≥ k if a > 0, y ≤ k if a < 0 | g(x) = 2(x – 1)² + 3 (a>0) | y ≥ 3 or [3, ∞) |
| Square Root Function | Non-negative real numbers | h(x) = √x | y ≥ 0 or [0, ∞) |
| Exponential Function (y=aˣ) | Positive real numbers | k(x) = 2ˣ | y > 0 or (0, ∞) |
| Logarithmic Function | All real numbers | m(x) = log(x) | ℝ or (-∞, ∞) |
| Rational Function | Solve for x in terms of y, then find domain restrictions for y (denominator ≠ 0) | n(x) = 1/x | ℝ except y = 0 or (-∞, 0) ∪ (0, ∞) |
How to Calculate the Range of a Function?
If your function fits one of the types listed above, you can directly apply the rules. Otherwise, consider graphing the function to visually identify the range.
Example 1: Range of a Quadratic Function
For f(x) = 2(x – 3)² – 5, using the rule for quadratic functions in vertex form, since a = 2 (positive), the parabola opens upwards, and the minimum value is k = -5. The range is y ≥ -5, or [-5, ∞).
Example 2: Range of a Logarithmic Function
For g(x) = ln(2x – 3) + 4, the range of any basic logarithmic function is all real numbers. The additional terms here do not change that fundamental range. So the range is ℝ or (-∞, ∞).
Methods to Calculate Domain and Range
Let’s illustrate with a discrete example before moving to continuous functions.
Suppose set X = {1, 2, 3, 4, 5} and set Y = {1, 2, 3, 4, 5, 6}. Consider a function f: X → Y defined by the rule y = x + 1.
- Domain = X = {1, 2, 3, 4, 5} (all input values from set X)
- Range = {f(1), f(2), f(3), f(4), f(5)} = {1+1, 2+1, 3+1, 4+1, 5+1} = {2, 3, 4, 5, 6} (corresponding output values)
Note that Y is the codomain, which is the set where the range exists, but it’s not necessarily equal to the range itself.
Now, let’s examine domain and range for specific types of continuous functions.
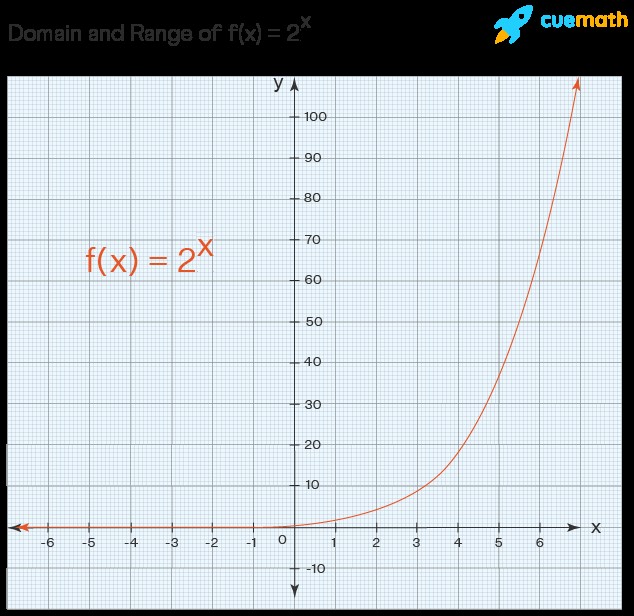
Domain and Range of Exponential Functions
Exponential functions, generally in the form y = aˣ (where a > 0 and a ≠ 1), have distinctive domain and range characteristics.
The function y = aˣ is defined for all real numbers x. Therefore, the domain of an exponential function is always all real numbers (ℝ).
Exponential functions always produce positive values. As x approaches negative infinity, aˣ approaches 0 but never actually reaches it. Thus, the range of an exponential function y = aˣ is all positive real numbers (0, ∞).
Example: Consider f(x) = 2ˣ.
- Domain: ℝ or (-∞, ∞)
- Range: (0, ∞)
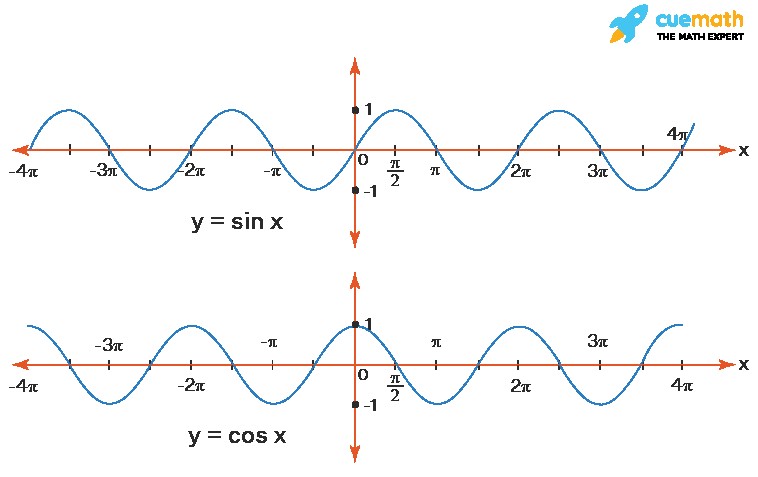
Domain and Range of Trigonometric Functions
Trigonometric functions like sine (sin θ) and cosine (cos θ) exhibit periodic behavior and have specific domain and range properties.
Sine and cosine functions are defined for all real numbers. Their values oscillate between -1 and 1.
For both sine and cosine functions:
- Domain: ℝ or (-∞, ∞)
- Range: [-1, 1]
Here’s a table summarizing the domain and range for all basic trigonometric functions:
| Trigonometric Function | Domain | Range |
|---|---|---|
| sin θ | (-∞, + ∞) | [-1, +1] |
| cos θ | (-∞, +∞) | [-1, +1] |
| tan θ | ℝ except (2n + 1)π/2, n∈ℤ | (-∞, +∞) |
| cot θ | ℝ except nπ, n∈ℤ | (-∞, +∞) |
| sec θ | ℝ except (2n + 1)π/2, n∈ℤ | (-∞, -1] ∪ [1, +∞) |
| cosec θ | ℝ except nπ, n∈ℤ | (-∞, -1] ∪ [1, +∞) |
Domain and Range of Absolute Value Functions
Absolute value functions, of the form y = |ax + b|, always return non-negative values.
The function y = |ax + b| is defined for all real numbers. So, the domain of an absolute value function is ℝ.
The absolute value of any expression is always greater than or equal to zero. Therefore, the range of an absolute value function y = |ax + b| is [0, ∞).
- Domain = ℝ or (-∞, ∞)
- Range = [0, ∞)
Example: Find the domain and range of f(x) = |6 – x|.
- Domain: ℝ
- Range: [0, ∞)
Domain and Range of Square Root Functions
Square root functions, in the form f(x) = √(ax + b), involve a restriction due to the nature of square roots in real numbers.
The square root of a negative number is not a real number. Thus, f(x) = √(ax + b) is defined only when ax + b ≥ 0. Solving this inequality gives the domain.
The square root of a non-negative number is always non-negative. Hence, the range of a square root function is always [0, ∞).
For f(x) = √(ax + b):
- Domain = x ≥ -b/a or [-b/a, ∞)
- Range = [0, ∞)
Example: Find the domain and range of h(x) = 2 – √(-3x + 2).
Domain: -3x + 2 ≥ 0 => -3x ≥ -2 => x ≤ 2/3. Domain = (-∞, 2/3].
Range: √(-3x + 2) ≥ 0 => -√(-3x + 2) ≤ 0 => 2 – √(-3x + 2) ≤ 2. Range = (-∞, 2].
Determining Domain and Range from Graphs
Graphs provide a visual way to understand domain and range.
- Domain from Graph: Look at all the x-values covered by the graph. Project the graph onto the x-axis; the covered interval(s) represent the domain.
- Range from Graph: Look at all the y-values covered by the graph. Project the graph onto the y-axis; the covered interval(s) represent the range.
When analyzing graphs, consider:
- Vertical Line Test: Ensure it’s a function (passes the vertical line test).
- Holes: Exclude x and y values corresponding to holes.
- Vertical Asymptotes: Exclude x-values of vertical asymptotes from the domain.
- Horizontal Asymptotes: Exclude y-values of horizontal asymptotes from the range.
- Discontinuities: Handle piecewise functions by considering each piece separately and using union (∪) to combine intervals.
- Arrows: Arrows indicate infinite extension in that direction.
Example 1:
- Domain: (-∞, ∞) (graph covers all x-values)
- Range: [0, ∞) (graph covers y-values from 0 upwards)
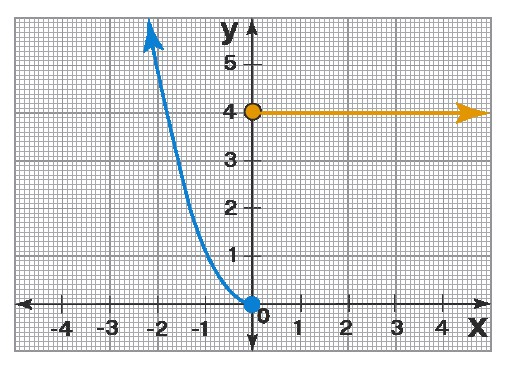
Example 2:
- Domain: [-5, ∞)
- Range: (-∞, 5]
Key takeaways:
- Domain: Possible inputs (x-values).
- Range: Possible outputs (y-values).
- Graphing is a powerful tool for visualizing range.
Frequently Asked Questions about Domain and Range
What is the Domain and Range of a Function?
The domain is the set of all possible input values (x-values) for which a function is defined. The range is the set of all possible output values (y-values) that the function can produce. For y = f(x), domain is the set of all permissible x values, and range is the set of all resulting f(x) values.
How Do You Write the Domain and Range?
Domain and range are written as sets, often using interval notation, set builder notation, or roster form. Interval notation uses brackets and parentheses to indicate inclusive and exclusive endpoints.
How to Find Domain and Range of a Graph?
For domain, examine the x-axis coverage of the graph. For range, examine the y-axis coverage. Consider any breaks, asymptotes, or endpoints.
What is The Domain and Range of a Constant Function?
For a constant function f(x) = k, the domain is all real numbers (ℝ) because you can input any x-value. The range is just {k}, a singleton set, as the output is always k, regardless of the input.
What is the Definition of Domain in Math?
In mathematics, the domain of a function is the set of all possible input values for which the function produces a valid output.
How to Find the Domain of a Function which is Rational?
For a rational function (a fraction where numerator and denominator are polynomials), the domain is all real numbers except for the values that make the denominator zero. Set the denominator ≠ 0 and solve for x to find the excluded values.
What are the Rules to Find the Domain of a Function?
General rules include:
- Polynomials: Domain is ℝ.
- Rational functions: Denominator ≠ 0.
- Square root functions: Expression under radical ≥ 0.
- Logarithmic functions: Argument > 0.
How to Find Domain and Range of Function?
To find the domain, identify restrictions on x-values that would make the function undefined (division by zero, square root of negative, etc.). To find the range, consider the possible y-values the function can output, often aided by graphing.
How to Find Range of a Rational Function?
Solve the rational function equation for x in terms of y. Then, determine the domain of this inverse relation in terms of y. This domain of the inverse relation is the range of the original function. Specifically, find the values of y that would make the denominator zero in the rearranged equation. These y-values are excluded from the range.
How to Find Domain and Range of an Equation?
For an equation y = f(x), find the domain by considering restrictions on x. To find the range, rearrange the equation to x = g(y) and find the domain of g(y) in terms of y.
How to Calculate the Domain and Range From the Graph of a Function?
Project the graph onto the x-axis to determine the domain and onto the y-axis to determine the range.
What is The Difference Between Domain and Range of a Function?
Domain is the set of inputs, range is the set of outputs. Domain is about what you can put into the function; range is about what you get out.
What is The Domain and Range of a Relation?
For a relation (set of ordered pairs), the domain is the set of all first elements (x-coordinates), and the range is the set of all second elements (y-coordinates).
What is the Domain and Range of Composite Functions?
For a composite function h(x) = (f ∘ g)(x) = f(g(x)), the domain of h is restricted by both the domain of g and the domain of f. Specifically, x must be in the domain of g, and g(x) must be in the domain of f. The range of h is a subset of the range of f.
What is the Domain and Range of a Quadratic Function?
For a quadratic function y = a(x – h)² + k, the domain is always ℝ. The range depends on the parabola’s orientation:
- If a > 0 (opens upwards), range is [k, ∞).
- If a < 0 (opens downwards), range is (-∞, k].
How to Find the Range of a Graph?
Visually inspect the graph and identify the lowest and highest y-values it reaches. The continuous set of these y-values constitutes the range.
Understanding domain and range is fundamental for working with functions in mathematics. By mastering these concepts, you gain a deeper insight into the behavior and characteristics of various functions.