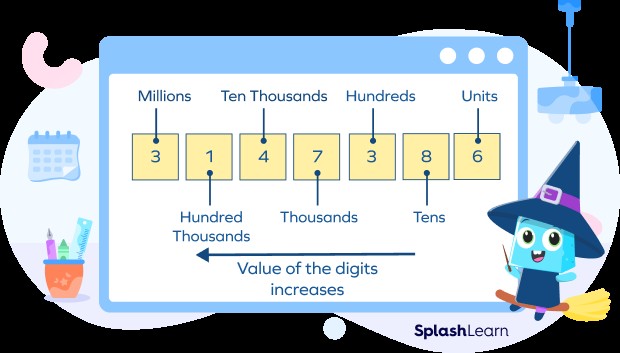
Expanded form is a fundamental concept in mathematics that helps us understand the value of each digit in a number. If you’re looking to grasp expanded form, its uses, and how it simplifies complex numbers, then WHAT.EDU.VN is here to guide you. We will explore how expanded form works, look at various examples, and provide resources for further learning.
Expanded form, also known as expanded notation, is a way of breaking down a number to show the value of each digit. It’s like taking a number apart and seeing what each piece is worth. This method is especially helpful for understanding place value and performing arithmetic operations. Let’s dive deeper into this topic and unravel its intricacies.
1. Understanding the Basics of Expanded Form
Expanded form is a way to represent a number as the sum of the values of its individual digits. This method highlights the place value of each digit, making it easier to understand the composition of the number.
For instance, the number 345 can be written in expanded form as:
300 + 40 + 5
This shows that 3 represents 300 (3 x 100), 4 represents 40 (4 x 10), and 5 represents 5 (5 x 1).
1.1. Place Value Explained
Place value is the foundation of expanded form. Each digit in a number has a specific place value depending on its position. Starting from the right, the place values are ones, tens, hundreds, thousands, and so on. Understanding place value is crucial for writing numbers in expanded form. Understanding place value is essential for mastering the expanded notation of numbers, helping with operations like addition, subtraction, multiplication, and division by breaking down numbers into manageable components.
- Ones: The rightmost digit represents the number of ones.
- Tens: The second digit from the right represents the number of tens.
- Hundreds: The third digit from the right represents the number of hundreds.
- Thousands: The fourth digit from the right represents the number of thousands.
1.2. How to Write Numbers in Expanded Form
To write a number in expanded form, follow these steps:
- Identify the place value of each digit in the number.
- Multiply each digit by its place value.
- Write the number as the sum of these values.
Example:
Let’s take the number 6,289.
- 6 is in the thousands place (6 x 1000 = 6000)
- 2 is in the hundreds place (2 x 100 = 200)
- 8 is in the tens place (8 x 10 = 80)
- 9 is in the ones place (9 x 1 = 9)
So, the expanded form of 6,289 is:
6000 + 200 + 80 + 9
2. Expanded Form with Whole Numbers
Expanded form is commonly used with whole numbers to break them down into their constituent parts. This is helpful for understanding the magnitude of each digit and performing arithmetic operations.
2.1. Examples of Expanded Form with Whole Numbers
Let’s look at some examples to illustrate how to write whole numbers in expanded form:
- 47: 40 + 7 (4 tens + 7 ones)
- 256: 200 + 50 + 6 (2 hundreds + 5 tens + 6 ones)
- 1,382: 1000 + 300 + 80 + 2 (1 thousand + 3 hundreds + 8 tens + 2 ones)
- 15,794: 10000 + 5000 + 700 + 90 + 4 (1 ten-thousand + 5 thousands + 7 hundreds + 9 tens + 4 ones)
- 328,451: 300000 + 20000 + 8000 + 400 + 50 + 1 (3 hundred-thousands + 2 ten-thousands + 8 thousands + 4 hundreds + 5 tens + 1 one)
2.2. Breaking Down Larger Numbers
Expanded form becomes particularly useful when dealing with larger numbers. It simplifies the process of understanding and working with these numbers. For instance:
- 1,234,567: 1000000 + 200000 + 30000 + 4000 + 500 + 60 + 7
This representation makes it clear that the number is composed of 1 million, 2 hundred-thousands, 3 ten-thousands, 4 thousands, 5 hundreds, 6 tens, and 7 ones.
3. Expanded Form with Decimals
Expanded form isn’t just for whole numbers; it also applies to decimals. When dealing with decimals, the place values extend to the right of the decimal point, representing tenths, hundredths, thousandths, and so on.
3.1. Understanding Decimal Place Values
To understand expanded form with decimals, it’s important to know the place values to the right of the decimal point:
- Tenths: The first digit to the right of the decimal point represents tenths (1/10 or 0.1).
- Hundredths: The second digit to the right of the decimal point represents hundredths (1/100 or 0.01).
- Thousandths: The third digit to the right of the decimal point represents thousandths (1/1000 or 0.001).
And so on, with each subsequent digit representing a smaller fraction of one.
3.2. Examples of Expanded Form with Decimals
Here are some examples of writing decimals in expanded form:
- 2.5: 2 + 0.5 (2 ones + 5 tenths)
- 7.38: 7 + 0.3 + 0.08 (7 ones + 3 tenths + 8 hundredths)
- 15.429: 10 + 5 + 0.4 + 0.02 + 0.009 (1 ten + 5 ones + 4 tenths + 2 hundredths + 9 thousandths)
- 0.675: 0.6 + 0.07 + 0.005 (6 tenths + 7 hundredths + 5 thousandths)
- 123.456: 100 + 20 + 3 + 0.4 + 0.05 + 0.006 (1 hundred + 2 tens + 3 ones + 4 tenths + 5 hundredths + 6 thousandths)
3.3. Decimals with Whole Numbers
When a number includes both whole numbers and decimals, the expanded form combines the principles of both. For example:
- 42.19: 40 + 2 + 0.1 + 0.09
Here, 42 is the whole number part, and 0.19 is the decimal part.
4. Why Use Expanded Form?
Expanded form is a valuable tool for several reasons:
- Understanding Place Value: It reinforces the understanding of place value, which is crucial for arithmetic operations.
- Simplifying Arithmetic: It can simplify addition, subtraction, multiplication, and division by breaking down numbers into more manageable components.
- Comparing Numbers: It makes it easier to compare numbers, especially when they have many digits.
- Teaching Tool: It’s an excellent teaching tool for helping students grasp the concept of number composition.
4.1. Benefits in Arithmetic Operations
Expanded form can be particularly helpful in arithmetic operations. For example, when adding two numbers, breaking them down into expanded form can make the process clearer:
Example:
Add 345 and 287 using expanded form:
- 345 = 300 + 40 + 5
- 287 = 200 + 80 + 7
Adding the corresponding parts:
- (300 + 200) + (40 + 80) + (5 + 7)
- 500 + 120 + 12
- 500 + 100 + 20 + 10 + 2
- 632
This approach can make complex additions more manageable, especially for learners who are still developing their arithmetic skills.
4.2. Comparing Numbers More Easily
When comparing numbers, expanded form can help identify the larger or smaller number more easily. By breaking down each number, you can compare the digits in each place value.
Example:
Compare 1,234 and 1,243:
- 1,234 = 1000 + 200 + 30 + 4
- 1,243 = 1000 + 200 + 40 + 3
By comparing the tens place, you can see that 40 is greater than 30, so 1,243 is greater than 1,234.
5. Expanded Form vs. Standard Form
It’s important to differentiate between expanded form and standard form:
- Standard Form: The usual way of writing numbers (e.g., 123, 4.56).
- Expanded Form: Writing the number as the sum of the values of its digits (e.g., 100 + 20 + 3, 4 + 0.5 + 0.06).
Standard form is compact and easy to read, while expanded form provides a detailed breakdown of the number.
5.1. Converting Between Expanded and Standard Forms
Converting between expanded and standard forms is a fundamental skill.
From Expanded to Standard Form:
Simply add the values in the expanded form together.
Example:
Convert 2000 + 300 + 50 + 8 to standard form:
2000 + 300 + 50 + 8 = 2358
From Standard to Expanded Form:
Follow the steps outlined earlier to break down the number into its constituent parts.
Example:
Convert 5,678 to expanded form:
5,678 = 5000 + 600 + 70 + 8
6. Common Mistakes to Avoid
When working with expanded form, there are some common mistakes to avoid:
- Incorrect Place Values: Ensure you correctly identify the place value of each digit.
- Missing Zeros: Don’t forget to include zeros for place values that don’t have a digit (e.g., in 1,056, include the 0 for the hundreds place).
- Decimal Point Errors: Pay close attention to the decimal point and ensure you’re using the correct decimal place values.
- Addition Errors: Double-check your addition when converting from expanded form to standard form.
6.1. Tips for Accuracy
To ensure accuracy when working with expanded form:
- Use a Place Value Chart: This can help you visually organize the place values of each digit.
- Double-Check Your Work: Always review your expanded form to ensure it accurately represents the original number.
- Practice Regularly: The more you practice, the more comfortable you’ll become with expanded form.
7. Advanced Applications of Expanded Form
Beyond basic arithmetic, expanded form has advanced applications in algebra and other areas of mathematics.
7.1. Expanded Form in Algebra
In algebra, expanded form can be used to simplify expressions and solve equations. For example, when dealing with polynomials, expanding them can make it easier to combine like terms.
Example:
Expand and simplify the expression (x + 2)(x + 3):
- (x + 2)(x + 3) = x(x + 3) + 2(x + 3)
- = x^2 + 3x + 2x + 6
- = x^2 + 5x + 6
Expanded form helps to break down the expression into simpler terms, making it easier to manipulate.
7.2. Expanded Form in Computer Science
In computer science, expanded form can be used to represent numbers in different bases, such as binary or hexadecimal. Understanding expanded form is essential for working with these number systems.
Example:
Represent the binary number 1011 in decimal form:
- 1011 (binary) = (1 x 2^3) + (0 x 2^2) + (1 x 2^1) + (1 x 2^0)
- = 8 + 0 + 2 + 1
- = 11 (decimal)
8. Real-World Examples of Expanded Form
Expanded form is not just a theoretical concept; it has practical applications in everyday life.
8.1. Financial Calculations
In financial calculations, expanded form can be used to understand the components of large sums of money. For example, when dealing with a loan or mortgage, breaking down the principal amount into expanded form can help understand the scale of the debt.
Example:
A mortgage of $250,000 can be understood as:
- $200,000 + $50,000 + $0 + $0 + $0
This breakdown can help visualize the magnitude of each part of the loan.
8.2. Measurement and Conversions
In measurement and conversions, expanded form can be used to break down units into smaller components. For example, when converting kilometers to meters, understanding the expanded form can simplify the process.
Example:
Convert 3.5 kilometers to meters:
-
- 5 km = 3 km + 0.5 km
- = (3 x 1000) meters + (0.5 x 1000) meters
- = 3000 meters + 500 meters
- = 3500 meters
9. Interactive Exercises to Practice Expanded Form
To reinforce your understanding of expanded form, try these interactive exercises:
- Write the following numbers in expanded form:
- 456
- 1,789
- 23.45
- 0.897
- Convert the following expanded forms to standard form:
- 500 + 70 + 2
- 1000 + 400 + 60 + 9
- 8 + 0.3 + 0.01
- 0.6 + 0.05 + 0.004
- Solve the following addition problems using expanded form:
- 123 + 456
- 789 + 321
- 45.6 + 78.9
9.1. Solutions to the Exercises
Here are the solutions to the interactive exercises:
- Expanded Form:
- 456 = 400 + 50 + 6
- 1,789 = 1000 + 700 + 80 + 9
- 23.45 = 20 + 3 + 0.4 + 0.05
- 0.897 = 0.8 + 0.09 + 0.007
- Standard Form:
- 500 + 70 + 2 = 572
- 1000 + 400 + 60 + 9 = 1469
- 8 + 0.3 + 0.01 = 8.31
- 0.6 + 0.05 + 0.004 = 0.654
- Addition with Expanded Form:
- 123 + 456 = (100 + 20 + 3) + (400 + 50 + 6) = 500 + 70 + 9 = 579
- 789 + 321 = (700 + 80 + 9) + (300 + 20 + 1) = 1000 + 100 + 10 = 1110
- 45.6 + 78.9 = (40 + 5 + 0.6) + (70 + 8 + 0.9) = 110 + 13 + 1.5 = 124.5
10. Resources for Further Learning
To deepen your understanding of expanded form, here are some resources:
- Online Math Tutorials: Websites like Khan Academy and Coursera offer comprehensive math tutorials that cover expanded form.
- Math Textbooks: Consult math textbooks for detailed explanations and examples of expanded form.
- Educational Websites: Websites like SplashLearn and Math Playground offer interactive games and worksheets to practice expanded form.
10.1. Additional Tips and Tricks
Here are some additional tips and tricks to help you master expanded form:
- Visualize Place Values: Use visual aids like place value charts to understand the position of each digit.
- Break Down Complex Numbers: Practice breaking down complex numbers into their expanded form to simplify arithmetic operations.
- Apply Expanded Form in Real-World Scenarios: Look for opportunities to use expanded form in everyday life, such as when calculating expenses or measuring distances.
11. The Importance of Understanding Numerical Notation
Understanding numerical notation, including expanded form, is vital for mathematical proficiency. It enhances problem-solving skills, supports further mathematical learning, and has practical applications in everyday life, from managing finances to understanding measurements.
11.1. Developing Problem-Solving Skills
Understanding expanded notation notation helps individuals develop strong problem-solving skills. By breaking down numbers into their constituent parts, learners can approach complex problems with greater clarity and confidence. This analytical approach is beneficial not only in mathematics but also in various other fields.
11.2. Foundation for Advanced Mathematics
Numerical notation serves as a foundation for advanced mathematics. Concepts like algebra, calculus, and statistics rely on a solid understanding of how numbers are constructed and manipulated. Mastering expanded notation early on sets the stage for success in these advanced topics.
11.3. Daily Life Applications
The ability to work with numbers effectively is essential in many aspects of daily life. Whether it’s managing personal finances, calculating grocery bills, or understanding statistical data, a strong grasp of numerical notation can make these tasks easier and more accurate.
12. Addressing Common Misconceptions About Numerical Notation
Several misconceptions exist regarding numerical notation, particularly with concepts like expanded form. Addressing these misconceptions is essential for fostering a clear and accurate understanding.
12.1. Misconception: Expanded Form Is Only for Beginners
One common misconception is that expanded form is only for beginners. While it’s often introduced in elementary school, expanded form is useful for simplifying complex arithmetic and algebraic problems. It provides a way to visualize the components of a number, making it valuable at all levels of mathematics.
12.2. Misconception: Expanded Form and Standard Form Are Unrelated
Another misconception is that expanded form and standard form are unrelated. In reality, they are two sides of the same coin. Expanded form breaks down a number into its constituent parts, while standard form presents the number as a whole. Understanding the relationship between these forms is key to mastering numerical notation.
12.3. Misconception: Decimals Cannot Be Written in Expanded Form
Many people believe that decimals cannot be written in expanded form. However, as discussed earlier, decimals can be easily represented in expanded form by understanding the place values to the right of the decimal point. This representation helps to clarify the magnitude of each digit in the decimal number.
13. The Role of Technology in Teaching and Learning Numerical Notation
Technology plays a significant role in teaching and learning numerical notation. Various tools and resources are available to enhance understanding and practice.
13.1. Online Educational Platforms
Online educational platforms like Khan Academy, Coursera, and Udemy offer comprehensive courses on numerical notation. These platforms provide video lessons, interactive exercises, and quizzes to help learners master the concepts.
13.2. Interactive Math Games
Interactive math games can make learning numerical notation more engaging and fun. Websites like SplashLearn, Math Playground, and Prodigy offer a variety of games that help learners practice expanded form and other numerical notation concepts in an entertaining way.
13.3. Mobile Apps for Math Practice
Mobile apps provide a convenient way to practice numerical notation on the go. Apps like Photomath, WolframAlpha, and Mathway can help learners solve problems and check their work.
14. Tips for Parents and Educators to Support Numerical Notation Learning
Parents and educators can play a crucial role in supporting the learning of numerical notation. Here are some tips to help:
14.1. Use Real-Life Examples
Connect numerical notation to real-life examples to make it more relatable and meaningful. For instance, use expanded form when discussing money, measurements, or time.
14.2. Provide Hands-On Activities
Engage learners in hands-on activities that reinforce numerical notation concepts. Use manipulatives like base-ten blocks to visualize place value and expanded form.
14.3. Encourage Regular Practice
Encourage regular practice to build fluency in numerical notation. Set aside dedicated time for math practice and provide plenty of opportunities for learners to work on problems independently.
15. The Future of Numerical Notation in Education
As education continues to evolve, the way numerical notation is taught and learned will likely change as well. Emerging trends and technologies will shape the future of this fundamental topic.
15.1. Personalized Learning Approaches
Personalized learning approaches tailor instruction to meet the individual needs of each learner. Adaptive learning platforms can assess a learner’s understanding of numerical notation and provide targeted practice to address any gaps in knowledge.
15.2. Integration of Artificial Intelligence
Artificial intelligence (AI) can play a significant role in teaching and learning numerical notation. AI-powered tutors can provide personalized feedback and support to learners, helping them master the concepts more effectively.
15.3. Emphasis on Conceptual Understanding
The future of numerical notation education will likely place a greater emphasis on conceptual understanding rather than rote memorization. By focusing on why numerical notation works and how it can be applied in real-world situations, educators can help learners develop a deeper and more meaningful understanding of mathematics.
16. Common Questions About Expanded Form
Let’s explore some frequently asked questions about expanded form to further clarify its concepts and applications. These questions cover a range of topics, from the basic definition to more complex uses and benefits.
16.1. What is the Definition of Expanded Form?
Expanded form is a method of expressing a number as the sum of the values of its individual digits. Each digit’s value is determined by its place value (ones, tens, hundreds, etc.). This representation helps to visualize the composition of the number.
16.2. How is Expanded Form Different from Standard Form?
Standard form is the typical way we write numbers (e.g., 345, 6.78), while expanded form breaks down the number into the sum of its digits based on their place values (e.g., 300 + 40 + 5). Standard form is compact and easy to read, whereas expanded form provides a detailed breakdown.
16.3. Can Expanded Form be Used with Decimal Numbers?
Yes, expanded form can be used with decimal numbers. The place values to the right of the decimal point are tenths, hundredths, thousandths, and so on. For example, the expanded form of 2.5 is 2 + 0.5, and the expanded form of 7.38 is 7 + 0.3 + 0.08.
16.4. Why is Expanded Form Important in Mathematics?
Expanded form is important because it reinforces the understanding of place value, simplifies arithmetic operations, aids in comparing numbers, and serves as an excellent teaching tool for understanding number composition.
16.5. How Can Expanded Form Help in Arithmetic Operations?
Expanded form simplifies arithmetic operations by breaking down numbers into more manageable components. For example, when adding 345 and 287, you can break them down into (300 + 40 + 5) + (200 + 80 + 7), making the addition clearer.
16.6. What are Some Common Mistakes to Avoid When Using Expanded Form?
Common mistakes include incorrect identification of place values, missing zeros for place values without a digit, decimal point errors, and addition errors when converting from expanded form to standard form.
16.7. How Can I Improve My Accuracy When Working with Expanded Form?
To improve accuracy, use a place value chart to visually organize the place values, double-check your work, and practice regularly. These steps will help you become more comfortable and proficient with expanded form.
16.8. Can Expanded Form Be Used in Algebra?
Yes, expanded form can be used in algebra to simplify expressions and solve equations. For example, expanding polynomials can make it easier to combine like terms and manipulate the expression.
16.9. Are There Any Real-World Applications of Expanded Form?
Yes, expanded form has real-world applications in financial calculations (understanding the components of large sums of money) and measurement and conversions (breaking down units into smaller components).
16.10. Where Can I Find More Resources to Learn About Expanded Form?
More resources can be found on online educational platforms like Khan Academy, in math textbooks, and on educational websites like SplashLearn and Math Playground, which offer interactive games and worksheets.
17. Practical Examples of Expanded Form in Daily Life
Expanded form isn’t just a theoretical concept; it’s a practical tool that can be applied in various everyday situations. Understanding how to use expanded form can help simplify complex numbers and make calculations easier.
17.1. Budgeting and Financial Planning
When creating a budget or planning finances, expanded form can help break down large sums of money into manageable components. For instance, if you have a monthly income of $3,500, you can think of it as:
- $3,000 (thousands) + $500 (hundreds) + $0 (tens) + $0 (ones)
This breakdown can help you allocate your funds more effectively and track where your money is going.
17.2. Calculating Large Purchases
When making a large purchase, such as a car or a house, expanded form can help you understand the total cost and the components that make up that cost. For example, if you’re buying a car for $25,750, you can break it down as:
- $20,000 (ten thousands) + $5,000 (thousands) + $700 (hundreds) + $50 (tens) + $0 (ones)
This can help you see the scale of each part of the loan and plan your payments accordingly.
17.3. Measurement and Conversions
Expanded form can be useful in measurement and conversions, especially when dealing with metric units. For instance, if you need to convert 4.2 kilometers to meters, you can use expanded form:
-
- 2 km = 4 km + 0.2 km
- = (4 x 1000) meters + (0.2 x 1000) meters
- = 4000 meters + 200 meters
- = 4200 meters
This makes the conversion process clearer and easier to understand.
17.4. Cooking and Baking
In cooking and baking, recipes often involve measurements that can be simplified using expanded form. For example, if a recipe calls for 2.75 cups of flour, you can think of it as:
- 2 cups + 0.75 cups
- = 2 cups + (0.75 x 1 cup)
- = 2 cups + (3/4 cup)
This can help you accurately measure the ingredients and ensure the recipe turns out correctly.
17.5. Understanding Scientific Notation
Expanded form is also useful for understanding scientific notation, which is used to represent very large or very small numbers. For example, the number 3.4 x 10^5 can be understood as:
-
- 4 x 100,000
- = 340,000
Breaking down the scientific notation into expanded form helps you grasp the magnitude of the number.
18. Advanced Techniques for Mastery of Expanded Form
To truly master expanded form, it’s essential to move beyond the basics and explore advanced techniques that enhance understanding and application. These techniques involve using expanded form in more complex mathematical scenarios and real-world situations.
18.1. Applying Expanded Form to Polynomials
Expanded form is particularly useful when working with polynomials in algebra. By expanding polynomial expressions, you can simplify them, combine like terms, and solve equations more effectively. For example, consider the polynomial expression (x + 2)(x + 3):
- (x + 2)(x + 3) = x(x + 3) + 2(x + 3)
- = x^2 + 3x + 2x + 6
- = x^2 + 5x + 6
Expanding the expression allows you to combine the ‘3x’ and ‘2x’ terms, resulting in a simplified form that’s easier to work with.
18.2. Utilizing Expanded Form in Calculus
In calculus, expanded form can be used to approximate functions and solve complex problems. For instance, Taylor series expansions use expanded form to represent functions as infinite sums of terms, making it easier to analyze and compute their values.
- f(x) = f(a) + f'(a)(x-a) + f”(a)(x-a)^2/2! + …
Each term in the Taylor series is an expansion of the function at a particular point, allowing for accurate approximations.
18.3. Understanding Financial Models
Financial models often involve complex calculations that can be simplified using expanded form. For example, when calculating compound interest, expanding the formula can help you understand how each component contributes to the final amount:
- A = P(1 + r/n)^(nt)
Where:
- A is the future value of the investment/loan, including interest
- P is the principal investment amount (the initial deposit or loan amount)
- r is the annual interest rate (as a decimal)
- n is the number of times that interest is compounded per year
- t is the number of years the money is invested or borrowed for
Expanding this formula can help visualize the impact of each variable on the final result.
18.4. Optimizing Computer Algorithms
In computer science, expanded form can be used to optimize algorithms and improve performance. By breaking down complex calculations into simpler steps, you can identify areas where the algorithm can be made more efficient.
For example, in signal processing, Fourier series expansions use expanded form to represent signals as sums of sine and cosine waves, allowing for efficient filtering and analysis.
18.5. Enhancing Data Analysis
Expanded form can also be applied in data analysis to simplify complex datasets and identify patterns. By breaking down the data into individual components, you can gain a deeper understanding of the underlying trends and relationships.
For instance, in statistical analysis, regression models use expanded form to represent the relationship between variables, allowing for accurate predictions and insights.
19. The Future of Expanded Form in Mathematics Education
As mathematics education evolves, expanded form will continue to play a crucial role in helping students develop a strong foundation in numerical concepts. The future of expanded form in mathematics education involves integrating new technologies, emphasizing conceptual understanding, and promoting real-world applications.
19.1. Integration of Technology
Technology will play an increasingly important role in teaching and learning expanded form. Interactive simulations, educational apps, and online platforms can provide students with engaging and personalized learning experiences.
For example, virtual manipulatives can help students visualize place value and expanded form, while adaptive learning systems can provide targeted feedback and support.
19.2. Emphasis on Conceptual Understanding
Future mathematics education will focus more on conceptual understanding rather than rote memorization. Students will be encouraged to explore why expanded form works and how it relates to other mathematical concepts.
This approach will help students develop a deeper and more meaningful understanding of numbers and operations.
19.3. Real-World Applications
Connecting expanded form to real-world applications will make it more relevant and engaging for students. By exploring how expanded form is used in finance, science, and engineering, students will see the value of this concept and be more motivated to learn it.
19.4. Collaborative Learning
Collaborative learning activities can help students develop a deeper understanding of expanded form. By working together to solve problems and explain their reasoning, students can learn from each other and build stronger communication skills.
19.5. Assessment and Feedback
Effective assessment and feedback are essential for monitoring student progress and identifying areas where they need additional support. Formative assessments, such as quizzes and class discussions, can provide valuable insights into student understanding.
20. Embrace Continuous Learning and Curiosity
Expanded form is a stepping stone to understanding more complex mathematical concepts. Never stop asking questions and seeking new ways to apply what you’ve learned.
At WHAT.EDU.VN, we’re committed to providing you with the knowledge and resources you need to succeed. If you have any questions or need further assistance, don’t hesitate to reach out. Our team of experts is here to help you every step of the way.
Do you have any burning questions? Visit WHAT.EDU.VN today and ask away! Our platform offers free answers to any question you might have.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn
Remember, learning is a journey, not a destination. Embrace the challenges, celebrate your successes, and never stop exploring the wonderful world of mathematics.