Are you curious about what linear algebra is and how it’s used? WHAT.EDU.VN offers clear explanations and free answers to all your questions. Discover the foundations of vector spaces, linear equations, and matrix transformations.
1. Understanding Linear Algebra: A Comprehensive Overview
Linear algebra is a branch of mathematics that focuses on the study of vectors, vector spaces, linear transformations, and systems of linear equations. It is a fundamental tool in many areas of science, technology, engineering, and mathematics (STEM), as well as in fields like economics and computer science.
1.1. The Core Concepts of Linear Algebra
At its heart, linear algebra deals with:
- Vectors: Objects that have both magnitude and direction, often represented as arrows or ordered lists of numbers.
- Vector Spaces: Collections of vectors that satisfy certain axioms, allowing for operations like addition and scalar multiplication.
- Linear Transformations: Functions that preserve vector addition and scalar multiplication, mapping one vector space to another.
- Matrices: Rectangular arrays of numbers used to represent linear transformations and solve systems of linear equations.
- Systems of Linear Equations: Sets of equations where the variables are raised to the power of one.
1.2. Why is Linear Algebra Important?
Linear algebra is essential because it provides a framework for modeling and solving problems involving linear relationships. These relationships are prevalent in many real-world applications, making linear algebra a powerful tool for:
- Solving Systems of Equations: Finding the values of variables that satisfy multiple linear equations simultaneously.
- Data Analysis: Performing operations on large datasets to extract meaningful information and patterns.
- Computer Graphics: Transforming and manipulating images and 3D models.
- Machine Learning: Developing algorithms for pattern recognition, classification, and prediction.
- Physics and Engineering: Modeling physical systems and solving problems in areas like mechanics, electromagnetism, and signal processing.
- Optimization: Finding the best solutions to problems with linear constraints.
1.3. Linear Algebra and WHAT.EDU.VN: Your Questions Answered
Have questions about linear algebra or need help with a specific problem? Don’t struggle alone. Visit WHAT.EDU.VN and ask your question for free. Get clear, concise answers from knowledgeable experts and join a community of learners.
2. Diving Deeper: Key Concepts in Linear Algebra Explained
To truly grasp what linear algebra is all about, let’s explore some of its fundamental concepts in more detail.
2.1. Vectors: The Building Blocks of Linear Algebra
A vector is an object that has both magnitude (length) and direction. Vectors can be represented geometrically as arrows or algebraically as ordered lists of numbers called components.
2.1.1. Vector Representation
- Geometric Representation: An arrow originating from a point (usually the origin) and pointing in a specific direction. The length of the arrow represents the magnitude of the vector.
- Algebraic Representation: An ordered list of numbers, such as (1, 2, 3) in three dimensions. Each number represents the component of the vector along a specific axis.
2.1.2. Vector Operations
-
Addition: Adding two vectors involves adding their corresponding components. For example, (1, 2) + (3, 4) = (4, 6). Geometrically, this corresponds to placing the tail of the second vector at the head of the first vector and drawing the resulting vector from the tail of the first to the head of the second.
Alternative text: Coordinate vector addition showing how vectors are added by adding their corresponding x and y coordinates.
-
Scalar Multiplication: Multiplying a vector by a scalar (a number) involves multiplying each component of the vector by the scalar. For example, 2 * (1, 2) = (2, 4). Geometrically, this corresponds to scaling the length of the vector by the scalar.
2.2. Vector Spaces: Abstracting the Concept of Space
A vector space is a set of vectors that satisfies certain axioms, allowing for operations like addition and scalar multiplication to be performed within the set. This abstract definition allows us to treat various mathematical objects as vectors, even if they are not traditional geometric vectors.
2.2.1. Axioms of a Vector Space
A vector space must satisfy the following axioms:
- Closure under Addition: If u and v are vectors in the space, then u + v is also in the space.
- Commutativity of Addition: u + v = v + u for all vectors u and v in the space.
- Associativity of Addition: (u + v) + w = u + (v + w) for all vectors u, v, and w in the space.
- Existence of Additive Identity: There exists a vector 0 in the space such that u + 0 = u for all vectors u in the space.
- Existence of Additive Inverse: For every vector u in the space, there exists a vector –u in the space such that u + (-u) = 0.
- Closure under Scalar Multiplication: If u is a vector in the space and c is a scalar, then *c*u is also in the space.
- Distributivity of Scalar Multiplication with respect to Vector Addition: c (u + v) = *cu + cv for all scalars c* and vectors u and v in the space.
- Distributivity of Scalar Multiplication with respect to Scalar Addition: (c + d) u = *cu + du for all scalars c and d* and vectors u in the space.
- Associativity of Scalar Multiplication: (c d) u = c (*du) for all scalars c and d* and vectors u in the space.
- Existence of Multiplicative Identity: 1u = u for all vectors u in the space, where 1 is the multiplicative identity scalar.
2.2.2. Examples of Vector Spaces
- Euclidean Space (R^n): The set of all n-tuples of real numbers, with component-wise addition and scalar multiplication.
- The Set of All Polynomials: Polynomials can be added and multiplied by scalars, satisfying the vector space axioms.
- The Set of All Continuous Functions: Continuous functions can be added and multiplied by scalars, also satisfying the vector space axioms.
2.3. Linear Transformations: Mapping Between Vector Spaces
A linear transformation is a function that maps vectors from one vector space to another, preserving the operations of vector addition and scalar multiplication.
2.3.1. Properties of Linear Transformations
A function T: V -> W is a linear transformation if it satisfies the following properties:
- Additivity: T(u + v) = T(u) + T(v) for all vectors u and v in V.
- Homogeneity: T(*cu) = cT(u) for all scalars c* and vectors u in V.
2.3.2. Examples of Linear Transformations
- Scaling: Multiplying a vector by a constant scales its length but preserves its direction.
- Rotation: Rotating a vector around the origin changes its direction but preserves its length.
- Projection: Projecting a vector onto a subspace maps it to its closest point in that subspace.
2.4. Matrices: Representing Linear Transformations
A matrix is a rectangular array of numbers that can be used to represent a linear transformation. Matrices provide a convenient way to perform computations and solve systems of linear equations.
2.4.1. Matrix Representation of Linear Transformations
Any linear transformation from R^n to R^m can be represented by an m x n matrix. The columns of the matrix represent the images of the standard basis vectors of R^n under the transformation.
2.4.2. Matrix Operations
- Addition: Adding two matrices of the same size involves adding their corresponding entries.
- Scalar Multiplication: Multiplying a matrix by a scalar involves multiplying each entry of the matrix by the scalar.
- Matrix Multiplication: Multiplying two matrices A and B is more complex and involves taking the dot product of the rows of A with the columns of B. Matrix multiplication represents the composition of linear transformations.
2.5. Systems of Linear Equations: Finding Solutions
A system of linear equations is a set of equations where the variables are raised to the power of one. Linear algebra provides methods for solving these systems and determining whether solutions exist.
2.5.1. Representing Systems of Linear Equations with Matrices
A system of linear equations can be represented in matrix form as Ax = b, where A is the coefficient matrix, x is the vector of variables, and b is the constant vector.
2.5.2. Methods for Solving Systems of Linear Equations
- Gaussian Elimination: A method for transforming the augmented matrix [A|b] into row echelon form, allowing for the solution to be easily determined.
- Matrix Inversion: If A is invertible, the solution can be found by multiplying both sides by the inverse of A: x = A^-1b.
- Cramer’s Rule: A method for solving systems of linear equations using determinants.
2.6. Still Confused? WHAT.EDU.VN is Here to Help
Linear algebra can be challenging, but you don’t have to face it alone. Visit WHAT.EDU.VN and ask your questions. Our experts provide clear explanations and step-by-step solutions to help you master this important subject.
3. Applications of Linear Algebra: Real-World Examples
Linear algebra is not just an abstract mathematical theory. It has numerous applications in various fields. Let’s explore some of the most important ones.
3.1. Computer Graphics and Image Processing
Linear algebra is fundamental to computer graphics and image processing. Transformations such as scaling, rotation, translation, and shearing can be represented by matrices.
3.1.1. Transformations in 2D and 3D
Matrices are used to transform points and objects in 2D and 3D space. By multiplying a point’s coordinates by a transformation matrix, the point can be moved, rotated, or scaled.
3.1.2. Image Filtering and Enhancement
Linear algebra techniques are used to filter and enhance images. For example, convolution operations can be represented as matrix multiplications.
3.2. Machine Learning and Data Analysis
Linear algebra is a cornerstone of machine learning and data analysis. Many machine learning algorithms rely on linear algebra for tasks such as dimensionality reduction, classification, and regression.
3.2.1. Dimensionality Reduction
Techniques like Principal Component Analysis (PCA) use linear algebra to reduce the number of variables in a dataset while preserving its essential information.
3.2.2. Classification and Regression
Linear regression and logistic regression are based on linear algebra. These algorithms use matrices to model the relationship between input variables and output variables.
3.3. Physics and Engineering
Linear algebra is used extensively in physics and engineering to model physical systems and solve problems in areas like mechanics, electromagnetism, and signal processing.
3.3.1. Mechanics
Linear algebra is used to analyze forces, moments, and stresses in mechanical systems.
3.3.2. Electromagnetism
Linear algebra is used to solve Maxwell’s equations, which describe the behavior of electromagnetic fields.
3.4. Economics and Finance
Linear algebra is used in economics and finance to model economic systems, analyze financial data, and optimize investment portfolios.
3.4.1. Economic Modeling
Linear algebra is used to model the relationships between different sectors of an economy.
3.4.2. Portfolio Optimization
Linear algebra is used to find the optimal allocation of assets in an investment portfolio.
3.5. Coding Theory
Linear algebra is crucial in coding theory, particularly in the construction and analysis of error-correcting codes used in data transmission and storage.
3.5.1. Linear Codes
Linear codes are a class of error-correcting codes that are based on linear algebra. They are widely used in digital communication systems to detect and correct errors introduced during transmission.
3.5.2. Generator and Parity-Check Matrices
Generator matrices are used to encode messages into codewords, while parity-check matrices are used to detect errors in received codewords. Both of these matrices are fundamental concepts in linear coding theory.
3.6. Unsure Where to Start? Ask WHAT.EDU.VN
With so many applications, linear algebra can seem overwhelming. Don’t worry, WHAT.EDU.VN is here to guide you. Ask your questions and get personalized advice from our experts.
4. Benefits of Learning Linear Algebra
Learning linear algebra offers numerous benefits, both in terms of career opportunities and intellectual development.
4.1. Enhanced Problem-Solving Skills
Linear algebra develops critical thinking and problem-solving skills that are valuable in any field.
4.1.1. Abstract Thinking
Linear algebra requires you to think abstractly and generalize concepts.
4.1.2. Logical Reasoning
Linear algebra emphasizes logical reasoning and deductive thinking.
4.2. Increased Career Opportunities
Linear algebra is a valuable skill in many high-demand fields, such as:
4.2.1. Data Science
Data scientists use linear algebra to analyze large datasets, build machine learning models, and extract insights.
4.2.2. Software Engineering
Software engineers use linear algebra to develop computer graphics, game engines, and other applications.
4.2.3. Financial Analysis
Financial analysts use linear algebra to model financial markets, analyze investment portfolios, and manage risk.
4.3. Deeper Understanding of Other Subjects
Linear algebra provides a foundation for understanding other advanced topics in mathematics, science, and engineering.
4.3.1. Calculus
Linear algebra is used in multivariable calculus to study linear approximations and transformations.
4.3.2. Differential Equations
Linear algebra is used to solve systems of linear differential equations.
4.4. Improved Analytical Skills
Learning linear algebra enhances your ability to analyze complex problems and make informed decisions.
4.4.1. Quantitative Analysis
Linear algebra provides tools for quantitative analysis and modeling.
4.4.2. Critical Thinking
Linear algebra encourages critical thinking and the ability to evaluate information objectively.
4.5. Ready to Take the Leap? WHAT.EDU.VN is Your Partner
Unlock your potential with linear algebra. WHAT.EDU.VN provides the resources and support you need to succeed. Ask your questions and start your learning journey today.
5. Common Challenges in Learning Linear Algebra
While linear algebra offers many benefits, it can also be a challenging subject for some learners. Understanding these challenges can help you overcome them and succeed in your studies.
5.1. Abstract Concepts
Linear algebra involves many abstract concepts that can be difficult to visualize and understand.
5.1.1. Vector Spaces
The concept of a vector space can be challenging for students who are used to working with concrete geometric vectors.
5.1.2. Linear Transformations
Understanding how linear transformations map vectors from one space to another requires abstract thinking.
5.2. Computational Complexity
Linear algebra involves many computations that can be tedious and error-prone.
5.2.1. Matrix Operations
Performing matrix addition, scalar multiplication, and matrix multiplication can be time-consuming and requires careful attention to detail.
5.2.2. Solving Systems of Equations
Solving systems of linear equations using Gaussian elimination or other methods can be complex and requires practice.
5.3. Notational Overload
Linear algebra uses a lot of notation that can be overwhelming for beginners.
5.3.1. Matrices and Vectors
Keeping track of the indices and dimensions of matrices and vectors can be challenging.
5.3.2. Linear Transformations and Operators
Understanding the notation used to represent linear transformations and operators requires familiarity with abstract mathematical concepts.
5.4. Lack of Intuition
Some learners struggle to develop an intuitive understanding of linear algebra concepts.
5.4.1. Geometric Interpretation
Visualizing the geometric interpretation of linear algebra concepts can be difficult for some students.
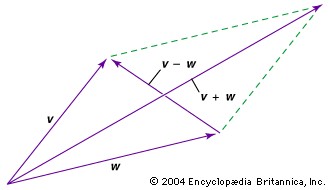Vector parallelogram for addition and subtraction
5.4.2. Real-World Applications
Connecting linear algebra concepts to real-world applications can help build intuition.
5.5. Stuck? WHAT.EDU.VN Offers a Helping Hand
Don’t let these challenges discourage you. WHAT.EDU.VN provides the support and resources you need to overcome them. Ask your questions and get personalized guidance from our experts.
6. Frequently Asked Questions About Linear Algebra (FAQs)
Here are some frequently asked questions about linear algebra to help you further understand this important subject.
| Question | Answer |
|---|---|
| What is the difference between a vector and a scalar? | A vector has both magnitude and direction, while a scalar has only magnitude. |
| What is a matrix? | A matrix is a rectangular array of numbers arranged in rows and columns. Matrices are used to represent linear transformations and solve systems of linear equations. |
| What is a linear transformation? | A linear transformation is a function that maps vectors from one vector space to another, preserving the operations of vector addition and scalar multiplication. |
| What is a system of linear equations? | A system of linear equations is a set of equations where the variables are raised to the power of one. |
| What are some applications of linear algebra? | Linear algebra has numerous applications in fields such as computer graphics, machine learning, physics, engineering, economics, and finance. |
| What is the importance of eigenvalues and eigenvectors? | Eigenvalues and eigenvectors are fundamental concepts in linear algebra that are used to analyze the behavior of linear transformations. They have applications in areas such as vibration analysis, quantum mechanics, and image compression. |
| How is linear algebra used in machine learning? | Linear algebra is used extensively in machine learning for tasks such as dimensionality reduction, classification, regression, and clustering. Many machine learning algorithms rely on linear algebra for their implementation. |
| What are some resources for learning linear algebra? | There are many resources available for learning linear algebra, including textbooks, online courses, video lectures, and software packages. Some popular resources include Gilbert Strang’s “Linear Algebra and Its Applications,” Khan Academy’s linear algebra course, and MIT OpenCourseWare’s linear algebra course. |
| What are some common mistakes to avoid when learning linear algebra? | Some common mistakes to avoid when learning linear algebra include not understanding the definitions of key concepts, making arithmetic errors when performing matrix operations, and not practicing enough problems. It is important to understand the underlying principles and to practice applying them to a variety of problems. |
| How can WHAT.EDU.VN help me with linear algebra? | WHAT.EDU.VN provides a platform for asking questions and receiving answers from experts in linear algebra. If you are struggling with a particular concept or problem, you can ask a question and receive personalized guidance. This can be a valuable resource for overcoming challenges and deepening your understanding of the subject. |
6.1. Still Have Questions? WHAT.EDU.VN is Your Go-To Resource
Don’t let unanswered questions hold you back. Visit WHAT.EDU.VN and ask your questions for free. Our experts are ready to provide clear, concise answers and help you master linear algebra.
7. Tips for Success in Linear Algebra
Here are some tips to help you succeed in your linear algebra studies:
7.1. Master the Fundamentals
Make sure you have a solid understanding of the basic concepts before moving on to more advanced topics.
7.1.1. Definitions and Theorems
Understand the definitions of key terms and the statements of important theorems.
7.1.2. Examples and Applications
Work through examples and applications to solidify your understanding of the concepts.
7.2. Practice Regularly
Practice solving problems regularly to develop your skills and build your intuition.
7.2.1. Textbook Problems
Work through the problems in your textbook and check your answers.
7.2.2. Online Resources
Use online resources to find additional problems and practice exercises.
7.3. Visualize Concepts
Try to visualize the geometric interpretation of linear algebra concepts whenever possible.
7.3.1. Graphing Vectors and Transformations
Graph vectors and transformations to see how they behave geometrically.
7.3.2. Using Software Tools
Use software tools to visualize matrices and linear transformations in 2D and 3D.
7.4. Seek Help When Needed
Don’t be afraid to ask for help when you are struggling with a concept or problem.
7.4.1. Ask Your Instructor
Ask your instructor for clarification during office hours or after class.
7.4.2. Use Online Forums and Communities
Participate in online forums and communities to ask questions and get help from other learners.
7.5. WHAT.EDU.VN: Your Learning Companion
Ready to conquer linear algebra? WHAT.EDU.VN is here to support you every step of the way. Ask your questions and get the personalized help you need to succeed.
8. Linear Algebra and the Future
Linear algebra is a dynamic field with ongoing research and development. Its importance is only likely to grow in the future, as it plays a crucial role in emerging technologies.
8.1. Quantum Computing
Linear algebra is fundamental to quantum computing, which uses quantum-mechanical phenomena to perform computations.
8.1.1. Qubits and Quantum States
Qubits, the basic units of quantum information, are represented as vectors in a complex vector space.
8.1.2. Quantum Gates
Quantum gates, which perform operations on qubits, are represented as unitary matrices.
8.2. Artificial Intelligence
Linear algebra is a core component of artificial intelligence (AI), particularly in areas such as deep learning and neural networks.
8.2.1. Neural Networks
Neural networks use linear algebra to perform matrix operations and compute the weights of connections between neurons.
8.2.2. Deep Learning
Deep learning algorithms rely on linear algebra for tasks such as image recognition, natural language processing, and machine translation.
8.3. Data Science and Big Data
Linear algebra is essential for analyzing large datasets and extracting meaningful insights.
8.3.1. Data Mining
Data mining techniques use linear algebra to identify patterns and relationships in large datasets.
8.3.2. Big Data Analytics
Big data analytics platforms rely on linear algebra for tasks such as data preprocessing, feature extraction, and model building.
8.4. A Skill for the Future: Learn with WHAT.EDU.VN
Equip yourself with the skills you need to thrive in the future. WHAT.EDU.VN offers the resources and support you need to master linear algebra and unlock your potential. Ask your questions and start your journey today.
9. Ready to Get Started? Ask Your Linear Algebra Questions on WHAT.EDU.VN
Do you have any questions about linear algebra? Are you struggling with a specific concept or problem? Don’t hesitate to ask for help.
WHAT.EDU.VN is a free online platform where you can ask any question and receive answers from knowledgeable experts. Our community is dedicated to helping you learn and understand linear algebra.
9.1. How to Ask a Question on WHAT.EDU.VN
- Visit WHAT.EDU.VN.
- Create a free account or log in.
- Click on the “Ask a Question” button.
- Enter your question in the text box. Be as specific as possible and provide any relevant context.
- Select the appropriate category for your question (e.g., Mathematics, Linear Algebra).
- Click on the “Submit” button.
9.2. What to Expect After Asking a Question
- Your question will be reviewed by our team of experts.
- You will receive an email notification when your question has been answered.
- You can view the answer to your question on the WHAT.EDU.VN website.
- You can ask follow-up questions or provide feedback on the answer.
9.3. Why Choose WHAT.EDU.VN?
- Free: Asking and answering questions is completely free.
- Expert Answers: Our team of experts is knowledgeable and experienced in linear algebra.
- Fast Response: We strive to answer questions as quickly as possible.
- Community Support: You can connect with other learners and share your knowledge.
- Convenient: You can access WHAT.EDU.VN from anywhere in the world.
9.4. Join the WHAT.EDU.VN Community Today
Don’t struggle with linear algebra alone. Join the WHAT.EDU.VN community and get the help you need to succeed.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Ready to start your linear algebra journey? Visit what.edu.vn and ask your first question today. We’re here to help you every step of the way.
