Perpendicular lines are fundamental in geometry and mathematics, forming the basis for understanding shapes, angles, and spatial relationships. Simply put, perpendicular lines are lines that intersect at a 90-degree angle, also known as a right angle. This concept is not just confined to textbooks; you can find perpendicular lines everywhere around you, from the corners of a room to the design of buildings and everyday objects.
Defining Perpendicular Lines: Intersecting at Right Angles
In mathematical terms, perpendicular lines are defined as two lines that meet or cross each other forming a right angle. A right angle is precisely 90 degrees. Think of it as the corner of a perfect square or rectangle. When two lines are perpendicular, they create this perfect corner at their point of intersection.
Alt text: Diagram illustrating two perpendicular lines, AB and CD, intersecting at a right angle, clearly marked with a 90-degree symbol.
The term “perpendicular” itself comes from the Latin word “perpendicularis,” which originally referred to a plumb line – a vertical line used to ensure walls are straight. This verticality perfectly embodies the concept of perpendicularity in geometry.
Symbol for Perpendicular Lines
To denote that two lines are perpendicular, we use a specific symbol: $bot$. So, if line AB is perpendicular to line CD, we write it as AB $bot$ CD. This symbol is a concise way to express the relationship between these lines in mathematical notations.
Perpendicular Lines in Everyday Life: Examples Around Us
Perpendicular lines aren’t just abstract geometric concepts; they are a part of our daily surroundings. Recognizing them in real-world scenarios helps solidify your understanding.
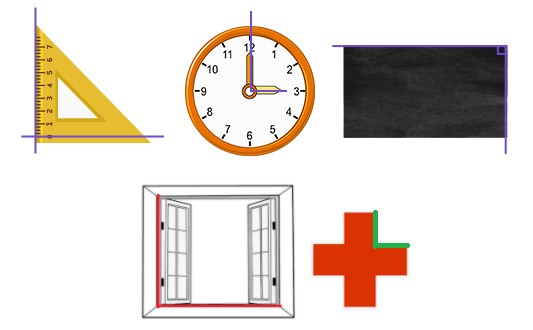
Here are some common examples of perpendicular lines you might encounter:
- Corners of Rectangular Objects: Look around your room. The corners of books, tables, windows, doors, and picture frames are all formed by perpendicular lines.
- Set Squares: Drafting tools like set squares are designed with perpendicular edges for precise drawing of right angles.
- Clock Hands at Specific Times: At 3:00 and 9:00, the hour and minute hands of an analog clock form a perfect right angle, showcasing perpendicularity.
- Cross Symbol: The iconic Red Cross symbol is a prime example of perpendicular lines intersecting at multiple right angles.
- Building Structures: Buildings rely heavily on perpendicularity. Walls are typically perpendicular to the ground, and floors are perpendicular to walls, ensuring structural stability.
- Grid Patterns: Many patterns, like those on graph paper or city street grids, are based on perpendicular lines creating organized and right-angled structures.
Key Properties of Perpendicular Lines
Understanding the properties of perpendicular lines is crucial for solving geometry problems and grasping related concepts.
- Right Angle Intersection: The defining property is that perpendicular lines always intersect at a right angle (90 degrees).
- Shortest Distance: The shortest distance from a point to a line is always along the perpendicular line from that point to the line. This principle is vital in various geometric and real-world applications, such as finding the altitude of a triangle or the shortest path to a road.
- Relationship with Parallel Lines: If two lines are perpendicular to the same line, then those two lines are parallel to each other. Imagine two vertical walls both perpendicular to the floor; those walls will be parallel.
Perpendicular vs. Parallel Lines: Key Differences
It’s easy to confuse perpendicular and parallel lines, but they are distinct concepts. Here’s a table summarizing their key differences:
| Feature | Perpendicular Lines | Parallel Lines |
|---|---|---|
| Intersection | Intersect at a 90-degree angle (right angle) | Never intersect, even when extended infinitely |
| Angle of Intersection | 90 degrees | 0 degrees (or 180 degrees, depending on direction) |
| Distance | Distance between them is zero at the point of intersection | Always maintain the same distance apart |
| Symbol | $bot$ | $left|right|$ |
| Examples | Corners of a square, clock hands at 3:00 | Railway tracks, opposite edges of a ruler |
Constructing Perpendicular Lines: Methods Explained
Knowing how to construct perpendicular lines is a valuable skill in geometry. There are two primary methods: using a protractor and using a compass and straightedge.
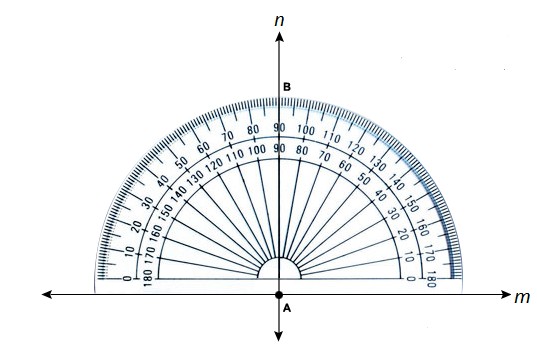
Method 1: Using a Protractor
A protractor is a tool specifically designed to measure angles, making it straightforward to construct perpendicular lines.
Steps:
- Start with a line: Draw a line and mark a point on it where you want to construct the perpendicular line. Let’s call the line ‘m’ and the point ‘A’.
- Position the protractor: Place the protractor on line ‘m’ so that its baseline aligns perfectly with line ‘m’, and the center of the protractor is exactly on point ‘A’.
- Mark 90 degrees: Locate the 90-degree mark on the protractor and make a point ‘B’ directly above this mark.
- Draw the perpendicular line: Remove the protractor and use a ruler or straightedge to draw a line connecting point ‘A’ and point ‘B’. This line, let’s call it ‘n’, is perpendicular to line ‘m’ at point ‘A’.
Method 2: Using a Compass and Straightedge
Constructing perpendicular lines with a compass and straightedge is a classic geometric method, relying on arcs and intersections to create the right angle.
Steps:
- Set the compass on the point: Place the compass point on point ‘A’ (the point on line ‘m’ where you want the perpendicular). Open the compass to a convenient radius and draw an arc that intersects line ‘m’ on both sides of point ‘A’. These intersection points create two new points equidistant from ‘A’.
- Increase compass radius and draw arcs: Slightly widen the compass radius. Place the compass point on each of the new intersection points (created in step 1) and draw arcs that intersect above line ‘m’. Ensure these arcs intersect each other.
- Draw the perpendicular line: Use a straightedge to draw a line connecting point ‘A’ to the point where the two arcs intersect (let’s call this intersection point ‘B’). Line AB is now perpendicular to line ‘m’ at point ‘A’.
Conclusion: Perpendicularity in Geometry and Beyond
Perpendicular lines are a cornerstone concept in geometry, essential for understanding angles, shapes, and spatial relationships. From their precise definition as lines intersecting at 90 degrees to their ubiquitous presence in the world around us, perpendicularity is a concept that bridges abstract mathematics and concrete reality. Whether you are studying geometry, architecture, engineering, or simply observing the world, recognizing and understanding perpendicular lines is a valuable skill.
Test Your Understanding: Practice Problems
Example 1: Identify Perpendicular or Parallel Lines
Determine whether each pair of lines shown below is perpendicular or parallel.
| (a) | (b) |
|---|---|
| (c) | (d) |
Solutions:
- Parallel
- Perpendicular
- Perpendicular
- Parallel
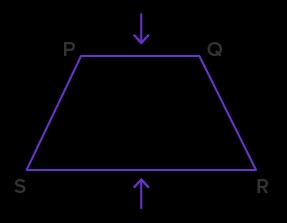
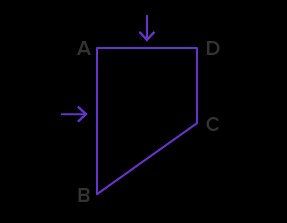
Example 2: Identify Perpendicular Relationships in Shapes
Write the relationship between the line segments indicated by arrows in each shape.
| (a) |
|—|—|
| (c) |
Solutions:
- AB $bot$ AE
- PQ $left|right|$ SR
- PQ $left|right|$ NM
- AB $bot$ AD
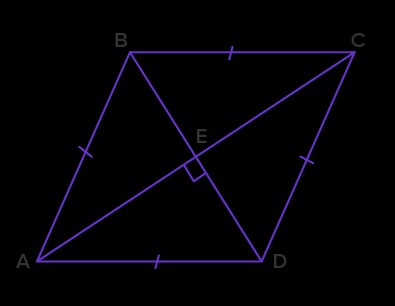
Example 3: Right Angles in a Rhombus
The diagonals of a rhombus are perpendicular to each other. How many right angles are formed at their intersection?
Solution: 4 right angles. $angle text{AED} = angle text{DEC} = angle text{CEB} = angle text{BEA} = 90$ degrees.
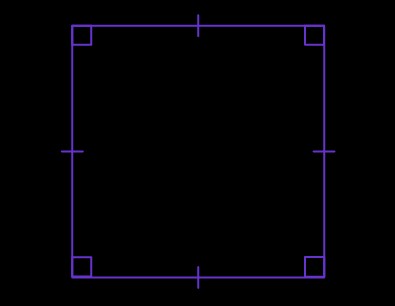
Example 4: Shapes with Perpendicular Lines
Name two-dimensional shapes that have perpendicular lines as part of their properties.
Solution: Rectangle, Square, Right-angled Triangle.
| |
|—|—|—|
Example 5: Deductive Reasoning with Perpendicular Lines
If AB $bot$ CD and CD $bot$ EF, what is the relationship between AB and EF?
Solution: AB and EF are parallel to each other.
Example 6 & 7: Identify Perpendicularity
Are these lines perpendicular? (Provide visual examples as in the original article).
Solutions: Example 6 – No, Example 7 – Yes.
Frequently Asked Questions (FAQs) About Perpendicular Lines
What are perpendicular lines?
Perpendicular lines are straight lines that intersect at a 90-degree angle, forming a right angle at their point of intersection.
Do perpendicular lines always have to intersect?
Yes, by definition, perpendicular lines must intersect. If lines do not intersect, they cannot be perpendicular.
What is the symbol used for perpendicular lines?
The symbol for perpendicular lines is $bot$.
What differentiates perpendicular lines from parallel lines?
Perpendicular lines intersect at a 90-degree angle, while parallel lines never intersect and remain equidistant from each other.
Are all intersecting lines perpendicular?
No, not all intersecting lines are perpendicular. Lines can intersect at various angles; only those intersecting at 90 degrees are considered perpendicular.
Can lines be both parallel and perpendicular?
No, lines cannot be both parallel and perpendicular to each other. These are mutually exclusive relationships.
How many perpendicular lines can you draw to a given line through a point on that line?
Only one unique perpendicular line can be drawn to a given line through a specific point on that line in a two-dimensional plane.
How many perpendicular lines can be drawn to a given line in general?
Infinitely many perpendicular lines can be drawn to a given line. For each point on the given line, you can draw one perpendicular line, and since a line contains infinite points, there are infinite perpendicular lines possible.
