Are you struggling with geometry and need a clear explanation of what perpendicular lines are? WHAT.EDU.VN is here to provide a comprehensive guide to perpendicular lines, including their definition, properties, and real-world examples. We aim to make understanding geometric concepts easier. Discover free answers and clear explanations on WHAT.EDU.VN. Uncover the secrets of right angles, intersecting lines, and orthogonal relationships today!
1. Understanding Perpendicular Lines: The Basics
Perpendicular lines are fundamental in geometry. They form the basis for many shapes and structures we see around us. Understanding what they are and how they work is crucial for anyone studying math or science.
1.1. Defining Perpendicular Lines
Perpendicular lines are defined as two lines that intersect each other at a right angle (90 degrees). This intersection creates a perfect “L” shape, a key characteristic of perpendicularity. According to Euclidean geometry, this precise angular relationship is what sets them apart from other intersecting lines.
1.2. The Origin of the Term
The word “perpendicular” comes from the Latin word “perpendicularis,” which means “plumb line.” A plumb line is a weight suspended from a line used to determine verticality. This connection to verticality highlights the right angle aspect of perpendicular lines.
1.3. Symbolism and Notation
In mathematical notation, the symbol “⊥” represents perpendicularity. For example, if line AB is perpendicular to line CD, it is written as AB ⊥ CD. This symbol provides a concise way to express the relationship between these lines.
2. Properties of Perpendicular Lines
Perpendicular lines have several important properties that define their behavior and relationship with other lines.
2.1. Right Angle Intersection
The most defining property is that they always intersect at a right angle (90 degrees). This is the primary criterion for determining if two lines are perpendicular.
2.2. Perpendicular to the Same Line
If two lines are perpendicular to the same line, they are parallel to each other. This means they will never intersect, maintaining a constant distance apart.
2.3. Forming Right Triangles
Perpendicular lines are often found in right triangles, where two sides of the triangle form a right angle.
2.4. Slope Relationship
In coordinate geometry, the slopes of perpendicular lines have a unique relationship. If the slope of one line is ‘m’, the slope of the perpendicular line is ‘-1/m’. This inverse reciprocal relationship is essential for analytical geometry.
3. Perpendicular Lines in Everyday Life
Perpendicular lines are not just abstract mathematical concepts. They are present in many objects and structures we encounter daily.
3.1. Architectural Structures
Buildings, bridges, and other architectural marvels rely heavily on perpendicular lines for stability and design. The walls of a building typically meet the floor at a right angle, ensuring structural integrity.
3.2. Furniture and Home Decor
Tables, chairs, and shelves often incorporate perpendicular lines in their construction. The legs of a table are perpendicular to the tabletop, providing a stable surface.
3.3. Road Intersections
Many road intersections are designed with perpendicular lines, allowing for efficient traffic flow and safe navigation.
3.4. Everyday Objects
Everyday objects like books, laptops, and picture frames have perpendicular edges.
4. Parallel vs. Perpendicular Lines
It’s important to differentiate perpendicular lines from parallel lines. They represent fundamentally different geometric relationships.
4.1. Definition Comparison
Parallel lines are lines in a plane that never intersect. Perpendicular lines intersect at a 90-degree angle.
4.2. Symbol Differences
The symbol for parallel lines is “||”, while the symbol for perpendicular lines is “⊥”.
4.3. Real-World Examples
Railway tracks are a classic example of parallel lines. The corner of a postcard illustrates perpendicular lines.
| Perpendicular lines | Parallel Lines |
|---|---|
| Perpendicular lines are lines that intersect at a 90 degrees angle. | Parallel lines are lines that are always the same distance apart. Parallel lines never intersect. |
| The symbol used to represent a perpendicular line is “$bot$”. | The symbol used to represent a parallel line is “$left|right|$”. |
| Example: The corner of postcard |



5. Constructing Perpendicular Lines
Creating perpendicular lines is a fundamental skill in geometry. There are two common methods to achieve this: using a protractor and using a compass.
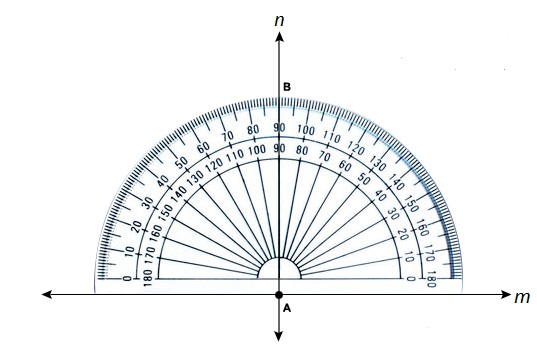
5.1. Using a Protractor
A protractor is a simple tool to measure angles.
Step 1: Draw a line and mark a point on it.
Step 2: Place the protractor’s base line along the line and the center on the point.
Step 3: Find the 90-degree mark and make a dot.
Step 4: Draw a line connecting the original point and the new dot. This line is perpendicular to the original line.
5.2. Using a Compass
A compass can create accurate perpendicular lines.
Step 1: Place the compass on the point. Draw arcs on both sides of the point.
Step 2: Widen the compass. Place the compass on the arcs to make intersecting arcs above the line.
Step 3: Connect the point to where the arcs intersect. This line is perpendicular.
6. Advanced Concepts Involving Perpendicular Lines
Perpendicularity extends beyond basic geometry and is crucial in advanced mathematical concepts.
6.1. Perpendicular Bisectors
A perpendicular bisector is a line that intersects a line segment at its midpoint, forming a right angle. It’s a crucial concept in constructions and proofs.
6.2. Orthogonal Vectors
In linear algebra, orthogonal vectors are vectors that are perpendicular to each other. Their dot product is zero, a fundamental property in vector spaces.
6.3. Normal Lines to Curves
In calculus, a normal line to a curve at a point is a line perpendicular to the tangent at that point. This concept is used in optimization problems and curve analysis.
6.4. Perpendicular Planes
In three-dimensional space, two planes are perpendicular if the angle between their normal vectors is 90 degrees. This is essential in 3D geometry and computer graphics.
7. Examples and Problem Solving
Understanding perpendicular lines is enhanced through practical examples. Let’s explore a few solved problems.
7.1. Identifying Perpendicular Lines
Determine whether the given lines are perpendicular or parallel.
(a) (b)
(c) (d)
Solution:
(a) Parallel lines
(b) Perpendicular lines
(c) Perpendicular lines
(d) Parallel lines
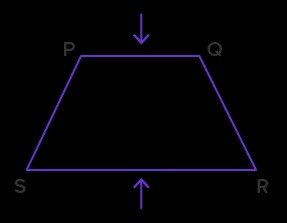
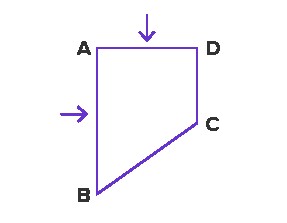
7.2. Line Segment Relations
Write the relation between the line segments indicated by the arrow in each shape.
(a)
(c)
Solution:
(a) AB ⊥ AE
(b) PQ || SR
(c) PQ || NM
(d) AB ⊥ AD
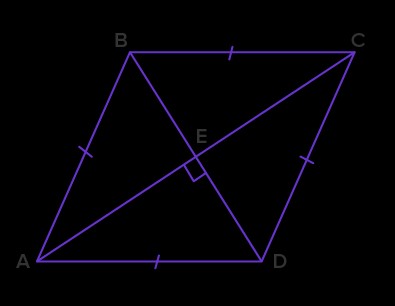
7.3. Diagonals of a Rhombus
The diagonals of a rhombus are perpendicular to each other. How many right angles are formed at the intersection?
Solution:
Since the lines AC and BD intersect each other at 90 degrees, there are 4 right angles at the intersecting point.
∠AED = ∠DEC = ∠CEB = ∠BEA = 90 degrees
8. Shapes with Perpendicular Lines
Several two-dimensional shapes prominently feature perpendicular lines.
8.1. Rectangle
A rectangle has four right angles, making its adjacent sides perpendicular.
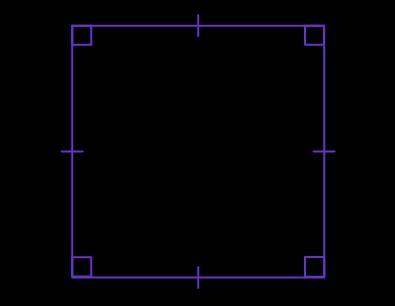
8.2. Square
A square, a special type of rectangle, also has four right angles and perpendicular sides.
8.3. Right-Angled Triangle
A right-angled triangle has one angle that is 90 degrees, meaning two of its sides are perpendicular.
9. Practice Problems
Test your understanding with these practice problems.
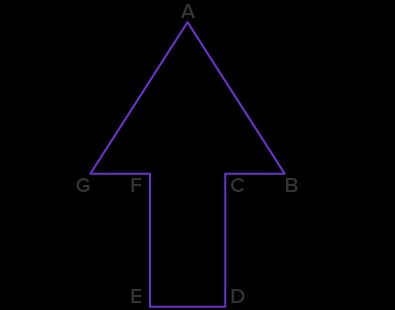
9.1. Identifying Perpendicular Segments
Identify the pair of perpendicular line segments in the given shape.
Answer: FE and ED are perpendicular line segments.
9.2. Real-World Objects
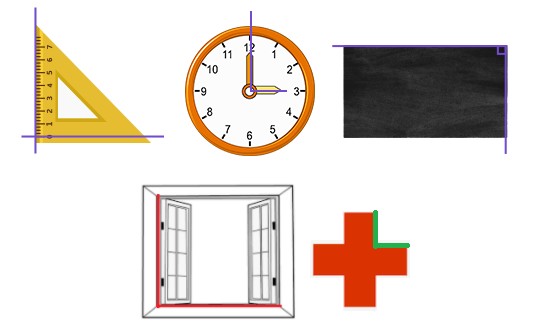
Which object’s highlighted pair of lines does NOT show perpendicular lines?
(A) (B)
(C)
Answer: A
9.3. Clock Hands
At what time will the hands of a clock be perpendicular to each other?
Answer: 3 o’clock
10. Frequently Asked Questions (FAQs)
10.1. What are perpendicular lines?
Perpendicular lines are two lines that intersect each other at a 90-degree angle.
10.2. Do perpendicular lines have to meet?
Yes, perpendicular lines always intersect at a right angle.
10.3. What is the perpendicular symbol?
The perpendicular symbol is “⊥”. It indicates that two lines are perpendicular to each other.
10.4. What is the difference between perpendicular and parallel lines?
Perpendicular lines intersect at right angles, while parallel lines never intersect and remain equidistant from each other.
10.5. Are all intersecting lines always perpendicular?
No, intersecting lines can meet at any angle. Only those that meet at 90 degrees are perpendicular.
11. The Role of Perpendicular Lines in Geometry
Perpendicular lines are foundational in geometry for several reasons.
11.1. Defining Shapes
They define shapes such as squares, rectangles, and right triangles. These shapes are fundamental in geometry and are used extensively in real-world applications.
11.2. Measuring Distances
The shortest distance from a point to a line is measured along the perpendicular line from the point to the line. This principle is used in various geometric problems and applications.
11.3. Coordinate Systems
Coordinate systems, such as the Cartesian plane, rely on perpendicular axes (x-axis and y-axis) to locate points in space.
11.4. Construction and Design
In construction and design, perpendicular lines are used to ensure structures are stable and aligned correctly.
12. Applications in Science and Engineering
Perpendicularity extends beyond mathematics and into various scientific and engineering fields.
12.1. Physics
In physics, perpendicular components of forces and velocities are often analyzed separately to simplify problem-solving. For example, projectile motion involves breaking down velocity into horizontal and vertical components, which are perpendicular to each other.
12.2. Engineering
Engineers use perpendicular lines in structural design to ensure that buildings and bridges can withstand forces and remain stable. The concept is also used in electrical engineering, where electric and magnetic fields can be perpendicular to each other in electromagnetic waves.
12.3. Computer Graphics
In computer graphics, perpendicularity is used to create realistic images and animations. Normal vectors, which are perpendicular to surfaces, are used to calculate lighting and shading effects.
12.4. Navigation
Perpendicular lines are used in navigation to determine directions and courses. For example, the shortest path between two points on a map is often a straight line, which can be represented using perpendicular components.
13. Teaching Perpendicular Lines to Children
Teaching perpendicular lines to children can be made fun and engaging through various activities and real-world examples.
13.1. Hands-On Activities
Use building blocks, craft sticks, or straws to create perpendicular lines and shapes. Allow children to physically manipulate these objects to understand the concept.
13.2. Real-World Examples
Point out examples of perpendicular lines in the classroom or at home. Windows, doors, and furniture can all be used as examples.
13.3. Drawing and Coloring
Have children draw shapes with perpendicular lines, such as squares, rectangles, and right triangles. Coloring these shapes can make the activity more engaging.
13.4. Games and Puzzles
Use games and puzzles that involve identifying perpendicular lines. This can make learning fun and reinforce the concept.
14. Common Misconceptions
It’s important to address common misconceptions about perpendicular lines to ensure a solid understanding.
14.1. All Intersecting Lines are Perpendicular
One common misconception is that all intersecting lines are perpendicular. It’s crucial to emphasize that perpendicular lines must intersect at a 90-degree angle.
14.2. Perpendicular Lines Must Be Horizontal and Vertical
Another misconception is that perpendicular lines must be horizontal and vertical. Perpendicular lines can be oriented in any direction as long as they intersect at a right angle.
14.3. Only Straight Lines Can Be Perpendicular
While the concept is typically introduced with straight lines, it’s important to note that curves can also be perpendicular at a point if their tangents at that point are perpendicular.
15. Further Exploration
To deepen your understanding of perpendicular lines, consider exploring these topics.
15.1. Coordinate Geometry
Study the relationship between perpendicular lines and their slopes in coordinate geometry.
15.2. Euclidean Geometry
Explore the theorems and postulates related to perpendicular lines in Euclidean geometry.
15.3. Trigonometry
Investigate the role of perpendicular lines in trigonometric functions and right triangle trigonometry.
15.4. Advanced Mathematics
Study advanced mathematical concepts that build upon the foundation of perpendicular lines, such as linear algebra and calculus.
16. Conclusion
Understanding perpendicular lines is essential for grasping fundamental concepts in geometry and mathematics. These lines are all around us, from the structures we build to the objects we use every day. By understanding their properties and applications, you can gain a deeper appreciation for the world around you.
Do you have more questions about geometry or any other topic? At WHAT.EDU.VN, we provide free and reliable answers to all your queries. Our platform is designed to make learning easy and accessible for everyone. Don’t hesitate to ask – we’re here to help!
Are you struggling to find quick, free answers to your questions? Do you feel lost and unsure where to turn for reliable information? Are you worried about the cost of getting expert advice?
Call To Action
Visit WHAT.EDU.VN today and experience the convenience of asking any question and receiving prompt, accurate answers from our community of knowledgeable experts. We’re here to help you navigate your challenges and find the solutions you need, all for free.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn