Point Slope Form is a powerful tool for defining linear equations, and WHAT.EDU.VN is here to help you master it. It allows you to write the equation of a line given its slope and a single point. Discover its formula, applications, and how it simplifies expressing linear relationships with practical examples to improve your understanding. Learn to use this form effectively with slope-intercept form and linear equations
1. Understanding the Essence of Point Slope Form
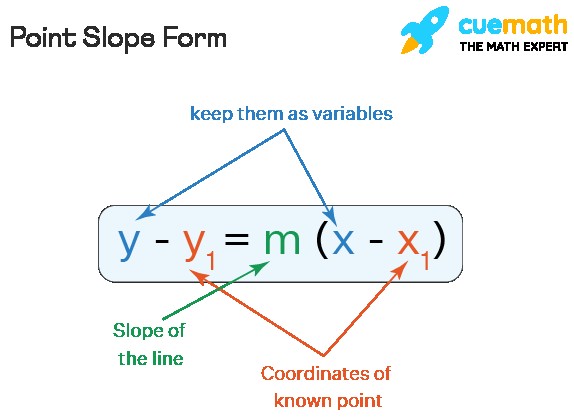
Point-slope form is a specific way to represent the equation of a straight line. It focuses on using the slope of the line and a particular point that the line passes through. This form is especially useful when you know the slope and a point, but not necessarily the y-intercept. It’s a fundamental concept in algebra and coordinate geometry, essential for understanding linear relationships. The point-slope form is expressed as:
y – y₁ = m(x – x₁)
where:
- (x, y) represents any point on the line.
- m stands for the slope of the line.
- (x₁, y₁) are the coordinates of a known point on the line.
2. The Point Slope Formula: A Deep Dive
The point slope formula is a cornerstone in linear algebra, used to determine the equation of a line when you know its slope and at least one point it passes through. This is especially useful in scenarios where the y-intercept isn’t immediately apparent. With this formula, the task of defining a linear equation becomes significantly easier.
2.1. Core Components of the Formula
The formula itself, y − y₁ = m (x − x₁), consists of several important elements:
- Variables (x, y): These represent any point on the line and remain variables in the final equation, showing the relationship between x and y for all points on the line.
- (x₁, y₁): This is a specific, known point on the line. Its coordinates are plugged into the formula to anchor the line in the coordinate plane.
- Slope (m): The slope defines the steepness and direction of the line. It indicates how much y changes for each unit change in x.
2.2. Mathematical Representation
Mathematically, the point slope formula is expressed as:
y − y₁ = m (x − x₁)
where:
- (x, y) is any point on the line.
- (x₁, y₁) is a known point on the line.
- m is the slope of the line.
This formula is particularly powerful because it directly incorporates the geometric properties of a line—its slope and a point it passes through—into its algebraic representation.
3. Unveiling the Derivation of the Point Slope Formula
To truly appreciate the point slope formula, it’s essential to understand how it’s derived. This derivation comes directly from the definition of slope itself, bridging the gap between geometric intuition and algebraic expression.
3.1. Understanding Slope
The slope of a line is defined as the change in the y-coordinate divided by the change in the x-coordinate between two points on the line. If we have two points, (x₁, y₁) and (x₂, y₂), the slope m is calculated as:
m = (y₂ – y₁) / (x₂ – x₁)
3.2. Deriving the Formula
Let’s say we know one point on the line, (x₁, y₁), and we want to find the equation that describes all other points (x, y) on the same line. We can use the slope formula, substituting (x, y) for (x₂, y₂):
m = (y – y₁) / (x – x₁)
To get the point slope form, we simply multiply both sides of the equation by (x – x₁):
m(x – x₁) = y – y₁
Rearranging the terms gives us the familiar point slope form:
y – y₁ = m(x – x₁)
4. Real-World Examples of the Point Slope Formula
To solidify your understanding of the point slope formula, let’s explore several practical examples. These examples will illustrate how to apply the formula and interpret the resulting equations.
4.1. Example 1: Finding the Equation of a Line
Problem: Determine the equation of a line that has a slope of 2 and passes through the point (3, 1).
Solution:
Using the point slope form, y – y₁ = m(x – x₁), we substitute m = 2, x₁ = 3, and y₁ = 1:
y – 1 = 2(x – 3)
This is the equation of the line in point slope form. If needed, you can convert it to slope-intercept form (y = mx + b) by simplifying:
y – 1 = 2x – 6
y = 2x – 5
4.2. Example 2: Application in Physics
Problem: In a physics experiment, the velocity of an object increases at a constant rate. At t = 2 seconds, the velocity is 5 m/s, and the acceleration (slope) is 3 m/s². Find the equation that describes the velocity (v) as a function of time (t).
Solution:
Here, acceleration is the slope (m = 3), and the point is (2, 5). Using the point slope form:
v – 5 = 3(t – 2)
Simplifying to slope-intercept form:
v – 5 = 3t – 6
v = 3t – 1
This equation tells us the velocity of the object at any time t.
4.3. Example 3: Real-World Scenario in Business
Problem: A business owner knows that after producing 100 units of a product, the profit is $500. The profit increases by $5 for each additional unit produced. Write an equation that models the profit (P) as a function of the number of units produced (u).
Solution:
The slope (m) is $5, and the point is (100, 500). Using the point slope form:
P – 500 = 5(u – 100)
Simplifying to slope-intercept form:
P – 500 = 5u – 500
P = 5u
This equation models the profit based on the number of units produced.
5. Step-by-Step Guide to Solving Problems Using Point Slope Form
Solving problems using the point slope form involves a systematic approach. This section provides a detailed, step-by-step guide to help you confidently tackle these problems.
-
Step 1: Identify the Given Information
- Start by carefully reading the problem to identify the slope (m) of the line and the coordinates of a point (x₁, y₁) that the line passes through.
- Sometimes, the slope might not be directly given but can be calculated from other information, such as two points on the line.
-
Step 2: Apply the Point Slope Formula
- Write down the point slope formula: y – y₁ = m(x – x₁).
- Substitute the identified values of m, x₁, and y₁ into the formula.
-
Step 3: Simplify the Equation
- Distribute the slope m across the terms inside the parentheses: y – y₁ = mx – mx₁.
- Rearrange the equation to isolate y and convert the equation into slope-intercept form (y = mx + b), which is often more convenient for graphing and analysis.
-
Step 4: Interpret the Result
- Once you have the equation in slope-intercept form, interpret the slope (m) and y-intercept (b) in the context of the problem.
- The slope represents the rate of change, and the y-intercept represents the value of y when x is zero.
5.1. Example
Find the equation of a line that passes through the point (2, -3) and has a slope of -1/2.
-
Solution:
-
Step 1: The given point is (x₁, y₁) = (2, -3), and the slope is m = -1/2.
-
Step 2: Substitute these values into the point slope formula: y – (-3) = -1/2(x – 2).
-
Step 3: Simplify the equation:
- y + 3 = -1/2x + 1
- y = -1/2x – 2
-
Step 4: The slope of the line is -1/2, and the y-intercept is -2. This line decreases as x increases, and it crosses the y-axis at y = -2.
-
6. Expanding Your Knowledge: Related Concepts
To gain a deeper understanding of point slope form, it’s beneficial to explore related concepts in linear algebra. This section introduces two key concepts: standard form and slope-intercept form.
6.1. Standard Form
The standard form of a linear equation is written as:
Ax + By = C
Where A, B, and C are constants, and A and B are not both zero. Converting from point slope form to standard form involves rearranging the equation to fit this format.
6.2. Slope-Intercept Form
The slope-intercept form is expressed as:
y = mx + b
Where m is the slope and b is the y-intercept. This form is particularly useful for quickly identifying the slope and y-intercept of a line, making it easy to graph and analyze.
7. Tackling Frequently Asked Questions (FAQs)
To further clarify your understanding of point slope form, let’s address some frequently asked questions.
7.1. What is the Point Slope Form of a Straight Line in Geometry?
The point slope form of a straight line is a way to express the equation of the line using its slope (m) and a known point (x₁, y₁) on the line. The formula is:
y – y₁ = m(x – x₁)
This form is useful when you have the slope and a point but need to find the equation of the line.
7.2. How Do You Find the Point Slope Form with a Point and Slope?
Finding the point slope form involves substituting the given point (x₁, y₁) and slope (m) into the formula:
y – y₁ = m(x – x₁)
Once you substitute these values, you have the equation of the line in point slope form.
7.3. How Do You Change Point Slope Form into Slope-Intercept Form?
To convert from point slope form to slope-intercept form (y = mx + b), you need to simplify the equation and isolate y. Here’s how:
Start with the point slope form: y – y₁ = m(x – x₁)
Distribute the slope m: y – y₁ = mx – mx₁
Add y₁ to both sides: y = mx – mx₁ + y₁
Rearrange to the slope-intercept form: y = mx + (y₁ – mx₁)
The term (y₁ – mx₁) is the y-intercept (b).
7.4. What is the Point Slope Formula?
The point slope formula is:
y – y₁ = m(x – x₁)
Where:
- (x, y) is any point on the line.
- (x₁, y₁) is a known point on the line.
- m is the slope of the line.
This formula is used to find the equation of a line when you know its slope and one point on it.
7.5. How Do You Write Point Slope Form of a Straight Line?
To write the point slope form, identify the slope (m) and a point (x₁, y₁) on the line. Then, substitute these values into the formula:
y – y₁ = m(x – x₁)
The resulting equation is the point slope form of the line.
7.6. How to Derive the Point Slope Formula?
The point slope formula is derived from the definition of slope. The slope (m) between two points (x₁, y₁) and (x, y) on a line is:
m = (y – y₁) / (x – x₁)
Multiplying both sides by (x – x₁) gives:
y – y₁ = m(x – x₁)
This is the point slope formula.
7.7. What are the Applications of Point Slope Formula?
The point slope formula has several applications:
- Finding the Equation of a Line: When you know the slope and a point on the line.
- Graphing a Line: When you have a point and the slope, you can easily graph the line.
- Calculating the Slope: If you have the equation in point slope form, you can quickly identify the slope.
7.8. How to Derive the Slope-Intercept Formula Using Point Slope Formula?
To derive the slope-intercept formula (y = mx + b) from the point slope formula (y – y₁ = m(x – x₁)), follow these steps:
Start with the point slope form: y – y₁ = m(x – x₁)
Distribute the slope m: y – y₁ = mx – mx₁
Add y₁ to both sides: y = mx – mx₁ + y₁
Rearrange to the slope-intercept form: y = mx + (y₁ – mx₁)
Here, b (the y-intercept) is equal to (y₁ – mx₁).
7.9. What is an Example of Point Slope Form?
For example, if a line has a slope of 3 and passes through the point (2, 1), the point slope form is:
y – 1 = 3(x – 2)
7.10. How Do You Find the Point Slope Form From a Graph?
To find the point slope form from a graph:
Identify a point (x₁, y₁) on the line.
Determine the slope (m) of the line. This can be done by finding two points on the line and using the formula: m = (y₂ – y₁) / (x₂ – x₁).
Substitute the point and slope into the point slope formula: y – y₁ = m(x – x₁).
8. Unlock Your Potential: Practice Questions
To reinforce your understanding of point slope form, here are some practice questions. Work through these problems to build your skills and confidence.
- Find the equation of a line that passes through the point (-1, 4) and has a slope of -2.
- Determine the equation of a line that passes through the points (3, -2) and (5, 4) using the point slope form.
- A line has a slope of 1/3 and passes through the point (6, -1). Find its equation in point slope form and convert it to slope-intercept form.
9. Need More Help? Ask WHAT.EDU.VN!
Do you have questions about point slope form or any other math topic? Don’t struggle alone! WHAT.EDU.VN is here to provide you with fast, free answers. Our community of experts is ready to help you understand complex concepts and solve challenging problems. Whether you’re a student, a professional, or just curious, we’re here to support your learning journey.
9.1. How WHAT.EDU.VN Can Help
- Free Answers: Get quick, reliable answers to your questions without any cost.
- Expert Support: Connect with knowledgeable experts who can guide you through difficult topics.
- Easy-to-Use Platform: Our website is designed to be user-friendly, making it simple to ask questions and find the information you need.
- Comprehensive Coverage: We cover a wide range of subjects, ensuring you can get help with all your learning needs.
9.2. Ready to Get Started?
- Visit our website: WHAT.EDU.VN
- Type your question in the search bar.
- Get your answer from our community of experts!
10. Contact Us
If you have any questions or need further assistance, don’t hesitate to reach out!
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: what.edu.vn
We’re here to help you succeed!