Prime number: are you curious about what they are and why they matter? WHAT.EDU.VN offers a simple explanation and clear examples to help you understand this essential math concept. Discover more about prime numbers and unlock the secrets of number theory with us; let’s dive into numerical exploration and mathematical analysis together.
1. What Are Prime Numbers?
A prime number is a whole number greater than 1 that has only two distinct positive divisors: 1 and itself. In simpler terms, a prime number can only be divided evenly by 1 and itself. This definition excludes 1, as it only has one divisor. Understanding prime numbers is essential for grasping concepts like prime factorization and cryptography. If you’re struggling with prime numbers or any other math questions, remember that WHAT.EDU.VN offers a platform where you can ask questions and receive answers from a community of knowledgeable individuals.
2. Prime Number Definition Explained
To fully grasp what prime numbers are, it’s helpful to break down the definition:
- Whole Number: Prime numbers are always positive whole numbers (also known as integers).
- Greater Than 1: The number 1 is not considered a prime number because it only has one divisor.
- Two Distinct Divisors: A prime number has exactly two different divisors: 1 and the number itself.
- Divisible Only by 1 and Itself: When you divide a prime number by any number other than 1 and itself, you will have a remainder (it’s not evenly divisible).
3. List of Prime Numbers
Identifying prime numbers can be tricky, but here’s a list to get you started. There are infinitely many prime numbers, but here are the first few:
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, and so on.
4. Properties of Prime Numbers
Prime numbers have unique properties that make them essential in number theory and various applications. Here are some key characteristics:
- Only Two Factors: By definition, prime numbers have only two factors: 1 and themselves.
- Infinitely Many: There is no largest prime number; they go on infinitely.
- Unique Factorization: Every integer greater than 1 can be written as a unique product of prime numbers (this is known as the Fundamental Theorem of Arithmetic).
- Even Prime: The number 2 is the only even prime number. All other even numbers are divisible by 2 and therefore have more than two factors.
- Distribution: Prime numbers become less frequent as numbers get larger.
5. Prime Numbers vs. Composite Numbers
Understanding the difference between prime and composite numbers is fundamental. A prime number has only two factors: 1 and itself. A composite number, on the other hand, has more than two factors.
| Feature | Prime Numbers | Composite Numbers |
|---|---|---|
| Definition | Has exactly two factors: 1 and itself. | Has more than two factors. |
| Examples | 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, etc. | 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, etc. |
| Smallest Number | 2 | 4 |
| Even Number | 2 (only even prime) | All other even numbers (except 2) |
| Factorization | Cannot be factored into smaller whole numbers. | Can be factored into smaller whole numbers. |
6. Prime and Co-Prime Numbers
It’s also important to distinguish between prime numbers and co-prime numbers.
| Feature | Prime Numbers | Co-Prime Numbers |
|---|---|---|
| Definition | A number that has only two factors: 1 and itself. | Two numbers whose greatest common factor (GCF) is 1. |
| Number of Numbers | Refers to a single number. | Always considered in pairs. |
| Factors | Only 1 and itself. | No common factor other than 1. |
| Prime or Composite | Must be a prime number. | Can be prime or composite. |
| Examples | 2, 3, 5, 7, 11, 13, 17, 19, 23, etc. | (8, 9), (15, 16), (21, 22), etc. |
7. Easy Ways to Find Prime Numbers
Finding prime numbers can seem daunting, but here are some strategies to simplify the process:
- Trial Division: Divide the number by all integers from 2 to the square root of the number. If none of these integers divide the number evenly, it is prime.
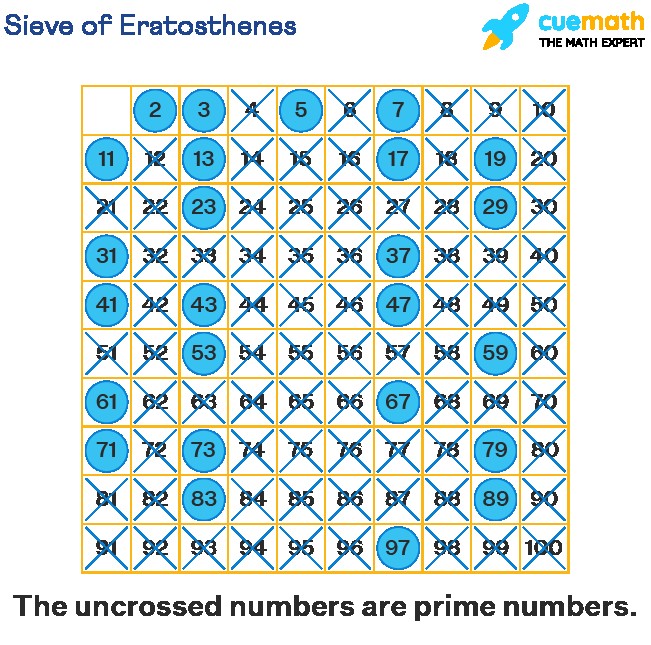
- Sieve of Eratosthenes: This ancient algorithm is useful for finding all prime numbers up to a specified limit. List all numbers from 2 to the limit, then iteratively mark as composite (not prime) the multiples of each prime, starting with the first prime number, 2.
- 6n ± 1 Rule: All prime numbers greater than 3 can be expressed in the form of 6n + 1 or 6n – 1, where n is any integer. However, not all numbers in this form are prime, so further testing is needed.
8. List of Odd Prime Numbers
All prime numbers except 2 are odd. Here’s a list of the first few odd prime numbers:
- 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
9. History of Prime Numbers
The study of prime numbers dates back to ancient times, with early evidence found in Egyptian papyri. The ancient Greeks, particularly Euclid, made significant contributions. Euclid proved that there are infinitely many prime numbers and developed several theorems related to prime numbers. Mathematicians continue to study prime numbers due to their fundamental role in number theory and their applications in cryptography and computer science.
10. Sieve of Eratosthenes: A Detailed Look
The Sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It works by iteratively marking the multiples of each prime, starting with the first prime number, 2. Here’s how it works:
- Create a List: Start with a list of consecutive integers from 2 to the specified limit.
- First Prime: Begin with the first prime number, 2.
- Mark Multiples: Mark all multiples of 2 as composite (not prime). That is, mark 4, 6, 8, 10, and so on.
- Next Prime: Find the next unmarked number after 2, which is 3. This is the next prime number.
- Mark Multiples: Mark all multiples of 3 as composite. That is, mark 6, 9, 12, 15, and so on.
- Repeat: Continue this process, finding the next unmarked number (which will be the next prime number) and marking its multiples as composite.
- Stop: Repeat until you’ve processed all numbers up to the square root of the limit.
- Remaining Numbers: All remaining unmarked numbers in the list are prime numbers.
11. Smallest Prime Number
The smallest prime number is 2. It is the only even prime number because all other even numbers are divisible by 2 and, therefore, have more than two factors.
12. Even Prime Number
The only even prime number is 2. All other even numbers are composite because they are divisible by 2, in addition to 1 and themselves.
13. Largest Prime Number
There is no largest prime number. Prime numbers are infinite, meaning they continue indefinitely. Mathematicians are continually discovering larger and larger prime numbers, but there will always be more.
14. Important Tips on Prime Numbers
- 2 is the only even prime number.
- The first few prime numbers are 2, 3, 5, 7, and 11.
- Not all prime numbers are odd (2 is an exception).
- 1 is neither a prime number nor a composite number.
- All prime numbers greater than 3 can be expressed in the form 6n + 1 or 6n – 1, where n is any integer.
15. Prime Number Examples
Let’s work through some examples to solidify your understanding:
Example 1: Is 37 a prime number?
To determine if 37 is prime, check if it has any factors other than 1 and 37. You only need to check divisibility by prime numbers less than the square root of 37 (which is approximately 6.08). The prime numbers less than 6.08 are 2, 3, and 5.
- 37 ÷ 2 = 18.5 (not divisible)
- 37 ÷ 3 = 12.33 (not divisible)
- 37 ÷ 5 = 7.4 (not divisible)
Since 37 is not divisible by any prime numbers less than its square root, it is a prime number.
Example 2: Is 51 a prime number?
To determine if 51 is prime, check if it has any factors other than 1 and 51.
- 51 ÷ 2 = 25.5 (not divisible)
- 51 ÷ 3 = 17 (divisible)
Since 51 is divisible by 3, it is a composite number, not a prime number.
Example 3: Identify all prime numbers between 20 and 30.
To find the prime numbers between 20 and 30, test each number for divisibility:
- 21 ÷ 3 = 7 (composite)
- 22 ÷ 2 = 11 (composite)
- 23 (prime)
- 24 ÷ 2 = 12 (composite)
- 25 ÷ 5 = 5 (composite)
- 26 ÷ 2 = 13 (composite)
- 27 ÷ 3 = 9 (composite)
- 28 ÷ 2 = 14 (composite)
- 29 (prime)
The prime numbers between 20 and 30 are 23 and 29.
16. Applications of Prime Numbers
Prime numbers might seem like an abstract concept, but they have practical applications in various fields:
- Cryptography: Prime numbers are fundamental to modern encryption algorithms, such as RSA. The difficulty of factoring large numbers into their prime factors is what makes these encryption methods secure.
- Computer Science: Prime numbers are used in hashing algorithms and random number generators.
- Number Theory: Prime numbers are a central topic in number theory, with many unsolved problems and conjectures revolving around them.
- Engineering: Prime numbers are sometimes used in designing mechanical systems to avoid resonance and ensure even wear.
- Biology: Some research suggests that prime numbers may play a role in biological processes, such as the life cycles of cicadas, which emerge in prime-numbered intervals (e.g., 13 years or 17 years) to avoid synchronization with predators.
17. Prime Number Practice Problems
Test your understanding with these practice problems:
- Which of the following numbers is prime: 14, 27, 31, or 39?
- List all prime numbers between 40 and 50.
- What is the smallest prime number greater than 50?
- Is 91 a prime number? Explain your answer.
- What are the first five prime numbers?
(Answers: 1. 31, 2. 41, 43, 47, 3. 53, 4. No, 91 = 7 x 13, 5. 2, 3, 5, 7, 11)
18. FAQ on Prime Numbers
Let’s address some frequently asked questions about prime numbers.
18.1. What are Prime Numbers in Math?
Prime numbers are whole numbers greater than 1 that have only two factors: 1 and the number itself.
18.2. What are the Examples of Prime Numbers?
Examples of prime numbers include 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
18.3. How to Find Prime Numbers?
To find prime numbers, you can use methods such as trial division or the Sieve of Eratosthenes. Trial division involves checking if a number is divisible by any integer from 2 to its square root. The Sieve of Eratosthenes is an ancient algorithm that efficiently finds all prime numbers up to a specified limit.
18.4. Why is 2 a Prime Number?
The number 2 is a prime number because it has exactly two factors: 1 and 2. It is also the only even prime number.
18.5. What are all the Prime Numbers from 1 to 100?
The prime numbers from 1 to 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
18.6. Which is the Smallest Prime Number?
The smallest prime number is 2.
18.7. What is the Difference Between a Prime and a Co-Prime Number?
A prime number has only two factors: 1 and itself. Co-prime numbers are two numbers that have no common factors other than 1. For example, 7 and 12 are co-prime because their only common factor is 1.
18.8. Can Prime Numbers be Negative?
No, prime numbers are defined as positive whole numbers greater than 1.
18.9. What are Twin Prime Numbers?
Twin prime numbers are pairs of prime numbers that differ by 2. For example, (3, 5), (5, 7), and (11, 13) are twin prime pairs.
18.10. Which of the Prime Numbers are Even Numbers?
The only even prime number is 2.
18.11. Which Numbers are not Prime Numbers?
Numbers that are not prime numbers are called composite numbers. Composite numbers have more than two factors. Examples include 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, and 20.
18.12. Are Prime Numbers Odd?
No, not all prime numbers are odd. The number 2 is an even prime number. All other prime numbers are odd.
18.13. Which is the First Prime Number?
The first prime number is 2.
18.14. What are the Even Prime Numbers from 1 to 100?
The only even prime number from 1 to 100 is 2.
18.15. What is the Greatest Prime Number Between 1 and 10?
The greatest prime number between 1 and 10 is 7.
19. Still Have Questions? Ask on WHAT.EDU.VN!
Do you have any more questions about prime numbers or any other topic? Don’t hesitate to ask on WHAT.EDU.VN! Our community of experts is ready to provide clear, accurate answers to help you learn and grow. Whether it’s math, science, history, or anything else, we’re here to help.
19.1. Why Choose WHAT.EDU.VN?
- Free Answers: Get answers to your questions without any cost.
- Expert Community: Connect with knowledgeable individuals who are passionate about sharing their expertise.
- Quick Responses: Receive timely answers to your questions.
- Easy to Use: Our platform is designed to be user-friendly and accessible for everyone.
19.2. How to Ask a Question on WHAT.EDU.VN
Asking a question on WHAT.EDU.VN is simple:
- Visit our website at WHAT.EDU.VN.
- Create an account or log in.
- Navigate to the “Ask a Question” section.
- Type in your question, providing as much detail as possible.
- Select the appropriate category for your question.
- Submit your question and wait for an answer from our community.
19.3. Join Our Community Today!
Join WHAT.EDU.VN today and become part of a community that values learning and sharing knowledge. Whether you’re a student, educator, or simply someone with a curious mind, you’ll find a welcoming and supportive environment.
Contact Us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Remember, curiosity is the key to learning. Don’t hesitate to ask any question that comes to mind. At what.edu.vn, we believe that everyone deserves access to free, accurate information. Join us today and start exploring the world of knowledge!