Probability is possibility! This mathematical concept predicts the likelihood of random events, offering solutions to uncertainties. At WHAT.EDU.VN, we simplify this fascinating topic, revealing its practical applications. Discover the power of probability and explore related concepts like expected value and statistical significance.
1. Probability Definition in Math
Probability, in mathematics, quantifies the likelihood of an event occurring. Unlike certain predictions, probability deals with events where outcomes are uncertain, expressing the chance of something happening. Its value ranges from 0 to 1, where 0 signifies impossibility and 1 signifies certainty. The sum of probabilities for all events within a sample space always equals 1.
For instance, flipping a coin yields two possible outcomes: heads or tails (H, T). However, flipping two coins results in four possibilities: {(H, H), (H, T), (T, H), (T, T)}.
2. Formula for Probability
The fundamental probability formula defines the likelihood of an event as the ratio of favorable outcomes to the total number of possible outcomes:
| Probability of event to happen P(E) = Number of favorable outcomes/Total Number of outcomes |
|---|

It’s important not to confuse “favorable outcome” with “desirable outcome”. This formula serves as the basis, with variations for specific situations and events.
3. Solved Examples
Let’s solidify understanding with practical examples:
Example 1: A bed contains 6 pillows: 3 red, 2 yellow, and 1 blue. What is the probability of randomly selecting a yellow pillow?
- Solution: Probability (Yellow) = (Number of yellow pillows) / (Total number of pillows) = 2/6 = 1/3.
Example 2: Imagine a container filled with colored bottles (red, blue, green, and orange). Sumit randomly picks and replaces bottles 1000 times, recording the following:
- Blue bottles: 300
- Red bottles: 200
- Green bottles: 450
- Orange bottles: 50
(a) What is the probability that Sumit will pick a green bottle?
- Solution: P(Green) = (Number of green bottles picked) / (Total bottles picked) = 450/1000 = 0.45
(b) If there are 100 bottles in the container, how many are likely to be green?
- Solution: Based on the experiment, 450 out of 1000 bottles are green. Therefore, approximately 45 out of 100 bottles are likely to be green.
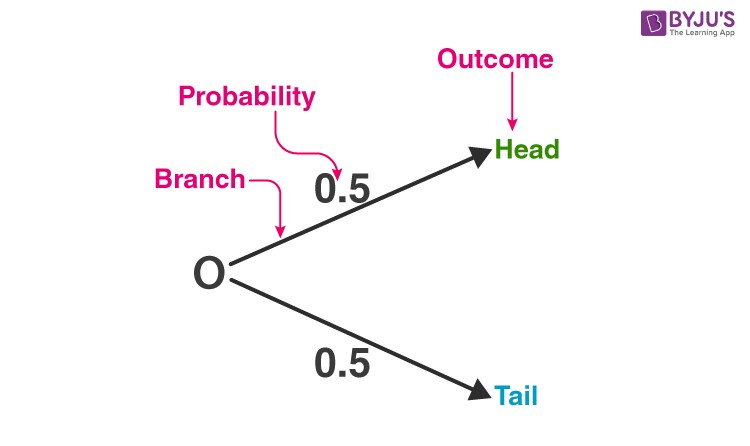
4. Probability Tree Diagrams
A tree diagram is a tool used to organize and visualize potential outcomes. These diagrams have branches representing probabilities and ends representing final outcomes. They are useful for determining when to multiply and when to add probabilities.
5. Types of Probability
Probability comes in different forms:
- Theoretical Probability
- Experimental Probability
- Axiomatic Probability
5.1. Theoretical Probability
Theoretical probability relies on reasoning about the likelihood of events. For instance, when tossing a fair coin, the theoretical probability of getting heads is 1/2.
5.2. Experimental Probability
Experimental probability is based on observations and experiments. It’s calculated by dividing the number of times an event occurs by the total number of trials. For example, if a coin is tossed 10 times and heads appears 6 times, the experimental probability of getting heads is 6/10 = 3/5.
5.3. Axiomatic Probability
Axiomatic probability uses a set of rules or axioms that apply universally. Developed by Kolmogorov, these axioms provide a rigorous framework for quantifying the chances of events occurring or not occurring.
6. Conditional Probability
Conditional probability refers to the probability of an event happening, given that another event has already occurred.
7. Probability of an Event
If an event E can occur in ‘r’ ways out of a total of ‘n’ equally likely possibilities, the probability of the event happening (success) is:
P(E) = r/n
The probability of the event not occurring (failure) is:
P(E’) = (n-r)/n = 1 – (r/n)
Where E’ signifies the event not occurring.
Therefore:
P(E) + P(E’) = 1
This signifies that the sum of all probabilities in a random experiment always equals 1.
8. What are Equally Likely Events?
Equally likely events have the same theoretical probability of occurring. In a sample space, outcomes are equally likely if they have equal probabilities.
For example, when rolling a fair die, each number (1 to 6) has a probability of 1/6 of appearing.
- Getting 3 and 5 on throwing a die
- Getting an even number and an odd number on a die
- Getting 1, 2 or 3 on rolling a die
These are examples of equally likely events.
9. Complementary Events
Complementary events involve only two outcomes: an event either occurs or does not occur. Examples include a person arriving or not arriving, getting a job or not getting a job. The complement of an event is simply the probability of that event not occurring.
- It will rain or not rain today
- The student will pass the exam or not pass.
- You win the lottery or you don’t.
10. Probability Theory
Probability theory originated in the 16th century with J. Cardan’s work, “The Book on Games of Chance.” It’s the branch of mathematics dealing with the likelihood of events. Probability theory uses axioms to define probability within a possibility space, assigning a probability measure between 0 and 1 to possible outcomes in a sample space.
11. Probability Density Function
The Probability Density Function (PDF) is a probability function showing the density of a continuous random variable within a certain range of values. It illustrates normal distribution and how mean and deviation are related. Standard normal distribution is used in statistics and science to represent real-valued variables with unknown distributions.
12. Probability Terms and Definition
Understanding key terms is essential:
| Term | Definition | Example |
|---|---|---|
| Sample Space | The set of all possible outcomes in a trial | 1. Tossing a coin, Sample Space (S) = {H,T} 2. Rolling a die, Sample Space (S) = {1,2,3,4,5,6} |
| Sample Point | A single possible result | In a deck of Cards: – 4 of hearts is a sample point. – The queen of clubs is a sample point. |
| Experiment/Trial | A series of actions with uncertain outcomes | The tossing of a coin, Selecting a card from a deck of cards, throwing a dice. |
| Event | A single outcome of an experiment | Getting a Heads while tossing a coin is an event. |
| Outcome | Possible result of a trial/experiment | T (tail) is a possible outcome when a coin is tossed. |
| Complementary Event | The non-happening events. The complement of an event A is the event, not A (or A’) | In a standard 52-card deck, A = Draw a heart, then A’ = Don’t draw a heart |
| Impossible Event | The event cannot happen | In tossing a coin, impossible to get both head and tail at the same time |
13. Applications of Probability
Probability is used in various real-life situations:
- Choosing a card from a deck
- Flipping a coin
- Throwing a die
- Pulling a ball from a bucket
13.1. Other Major Applications of Probability
- Risk assessment and modeling in industries
- Weather forecasting
- Predicting team wins in sports
- Share market analysis
14. Problems and Solutions on Probability
Let’s reinforce understanding with more examples:
Question 1: Find the probability of rolling a ‘3’ on a standard six-sided die.
Solution:
- Sample Space = S = {1, 2, 3, 4, 5, 6}
- Total number of outcomes = n(S) = 6
- Let A be the event of getting a 3.
- Number of favorable outcomes = n(A) = 1, i.e., A = {3}
- Probability, P(A) = n(A)/n(S) = 1/6
Therefore, P(getting 3 on rolling a die) = 1/6
Question 2: If you randomly draw a card from a standard deck, what is the probability that the card is a face card (Jack, Queen, or King)?
Solution:
- A standard deck has 52 cards.
- Total number of outcomes = n(S) = 52
- Let E be the event of drawing a face card.
- Number of favorable events = n(E) = 4 x 3 = 12 (4 suits x 3 face cards per suit)
- Probability, P(E) = n(E)/n(S) = 12/52 = 3/13
P(the card drawn is a face card) = 3/13
Question 3: A vessel contains 4 blue balls, 5 red balls, and 11 white balls. If three balls are drawn randomly, what is the probability that the first ball is red, the second ball is blue, and the third ball is white?
Solution:
- Probability (1st ball is red) = 5/20
- After drawing one red ball, the probability (2nd ball is blue) = 4/19
- After drawing a red and a blue ball, the probability (3rd ball is white) = 11/18
Therefore, the combined probability = (5/20) (4/19) (11/18) = 44/1368 = 0.032 or 3.2%
Question 4: Two dice are rolled. Find the probability that the sum is:
- Equal to 1
- Equal to 4
- Less than 13
Solution:
First, define the sample space S of rolling two dice:
S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2),(4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }
So, n(S) = 36
- Let E be the event “sum equal to 1”. Since no outcomes have a sum equal to 1:
P(E) = n(E) / n(S) = 0 / 36 = 0
- Let A be the event of the sum of numbers on dice equal to 4:
A = {(1,3),(2,2),(3,1)}
n(A) = 3
Hence, P(A) = n(A) / n(S) = 3 / 36 = 1 / 12
- Let B be the event of getting the sum of numbers on dice less than 13. Since the maximum sum possible is 12 (6+6), all outcomes have a sum less than 13:
n(B) = 36
Hence, P(B) = n(B) / n(S) = 36 / 36 = 1
15. Frequently Asked Questions (FAQs) on Probability
Here are some common questions about probability:
| Question | Answer |
|---|---|
| What Is Probability? Give an example | Probability is a branch of mathematics dealing with the likelihood of random events. Example: Tossing a coin, the possible outcomes are Head and Tail. |
| What is the formula of probability? | Probability = Number of favorable outcomes / Total number of outcomes |
| What are the different types of probability? | Theoretical Probability, Experimental Probability, Axiomatic Probability |
| What are the basic rules of probability? | If A and B are two events, then; P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) and P ( A ∩ B ) = P ( B ) ⋅ P ( A |
| What is the complement rule in probability? | P(A) + P(A’) = 1, where A is an event and A’ is its complement. |
| What are the different ways to present the probability value? | Percentage, Ratio, Decimal or fraction |
| What does the probability of 0 represent? | The event will not happen; it is an impossible event. |
| What is the sample space for tossing two coins? | S = {HH, HT, TH, TT} |
Do you have burning questions about probability or any other topic? Visit WHAT.EDU.VN and ask away! Our platform offers a FREE service where you can get answers from knowledgeable individuals. Stop struggling and start learning today!
Contact us at:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: what.edu.vn