What Is Radius? Discover the definition, formulas, and practical applications of the radius in circles, spheres, and beyond with WHAT.EDU.VN. Uncover the relationship between radius, diameter, circumference, and area, and learn how to calculate it effortlessly. Seeking quick answers and reliable information?
1. What is Radius? A Comprehensive Exploration
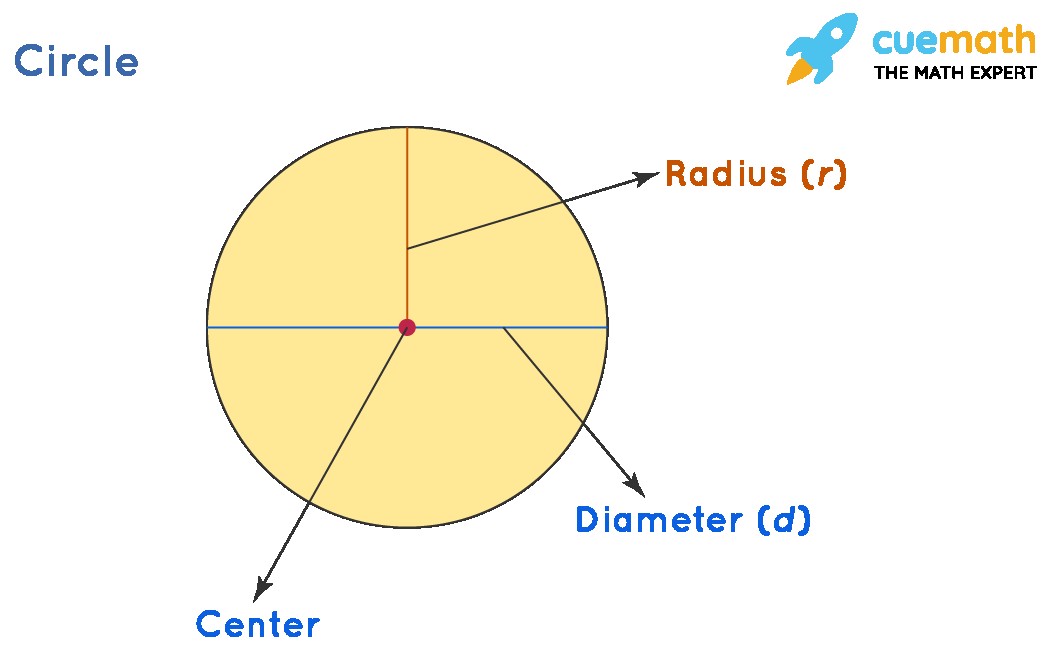
The radius, a fundamental concept in geometry, is a line segment that connects the center of a circle or sphere to any point on its circumference or surface. It’s a key element in defining the size and properties of these shapes. Think of it as the “reach” from the heart of a circle to its edge. The term “radius” comes from the Latin word meaning “ray” or “spoke of a wheel,” aptly describing its visual representation.
1.1. Defining Radius in Simple Terms
In simpler terms, imagine drawing a straight line from the very center of a circle to any point on the circle’s edge. That line, that distance, is the radius. It’s the same no matter where you draw that line to on the circle.
1.2. Radius vs. Diameter: Understanding the Difference
The diameter is a line segment that passes through the center of the circle and connects two points on the circumference. It’s essentially two radii joined end-to-end. Therefore, the diameter is always twice the length of the radius. Understanding this relationship is crucial for solving many geometry problems.
1.3. Why is the Radius Important?
The radius is not just a line segment; it’s a fundamental property that determines many other characteristics of a circle or sphere. It’s used to calculate:
- Circumference: The distance around the circle.
- Area: The amount of space enclosed by the circle.
- Volume (for spheres): The amount of space the sphere occupies.
- Surface Area (for spheres): The total area of the outer surface of the sphere.
Without the radius, calculating these crucial measurements would be impossible.
1.4. The Radius in Real-World Applications
The radius isn’t just a theoretical concept; it has practical applications in various fields, including:
- Engineering: Designing circular structures, calculating stress distribution in round objects.
- Architecture: Planning domes, arches, and other curved shapes.
- Physics: Calculating the trajectory of projectiles, understanding wave propagation.
- Astronomy: Measuring the size of celestial objects, calculating orbital paths.
- Everyday Life: Determining the size of pizzas, measuring the turning radius of a car.
2. Radius of Circle Formulas: Your Toolkit for Calculation
Calculating the radius is easy when you have the right information. Here’s a breakdown of the most common formulas:
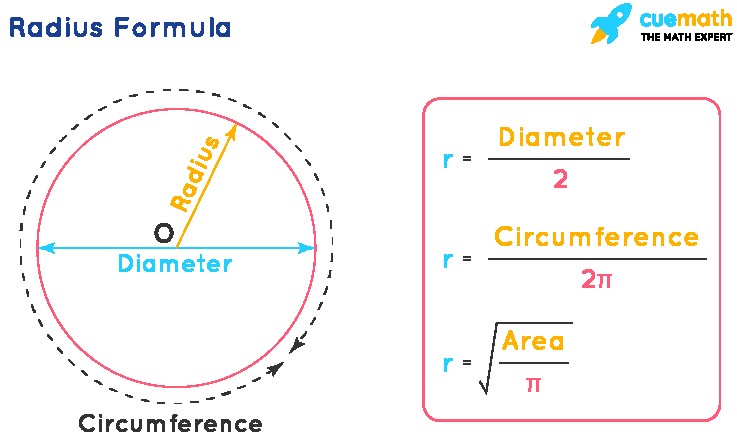
2.1. Radius Formula with Diameter
As mentioned earlier, the diameter is twice the radius. Therefore, the radius can be calculated by dividing the diameter by 2:
-
Radius = Diameter / 2
This is the simplest and most straightforward way to find the radius if you know the diameter.
2.2. Radius Formula from Circumference
The circumference (C) of a circle is the distance around it. The formula for circumference is: C = 2πr, where π (pi) is a mathematical constant approximately equal to 3.14159. To find the radius when you know the circumference, rearrange the formula:
-
Radius = Circumference / (2π)
This formula allows you to determine the radius from the circle’s perimeter.
2.3. Radius Formula using Area
The area (A) of a circle is the amount of space it occupies. The formula for the area is: A = πr². To find the radius when you know the area, rearrange the formula:
-
Radius = √(Area / π)
This formula involves taking the square root of the area divided by pi.
2.4. Summarizing the Radius Formulas
| Given | Formula | Explanation |
|---|---|---|
| Diameter | Radius = Diameter / 2 | Divide the diameter by 2 to get the radius. |
| Circumference | Radius = Circumference / (2π) | Divide the circumference by 2π to get the radius. |
| Area | Radius = √(Area / π) | Divide the area by π and take the square root to get the radius. |
3. Radius of a Circle: Delving Deeper
The radius isn’t just a number; it’s a defining characteristic of a circle. Understanding its properties is essential for grasping circular geometry.
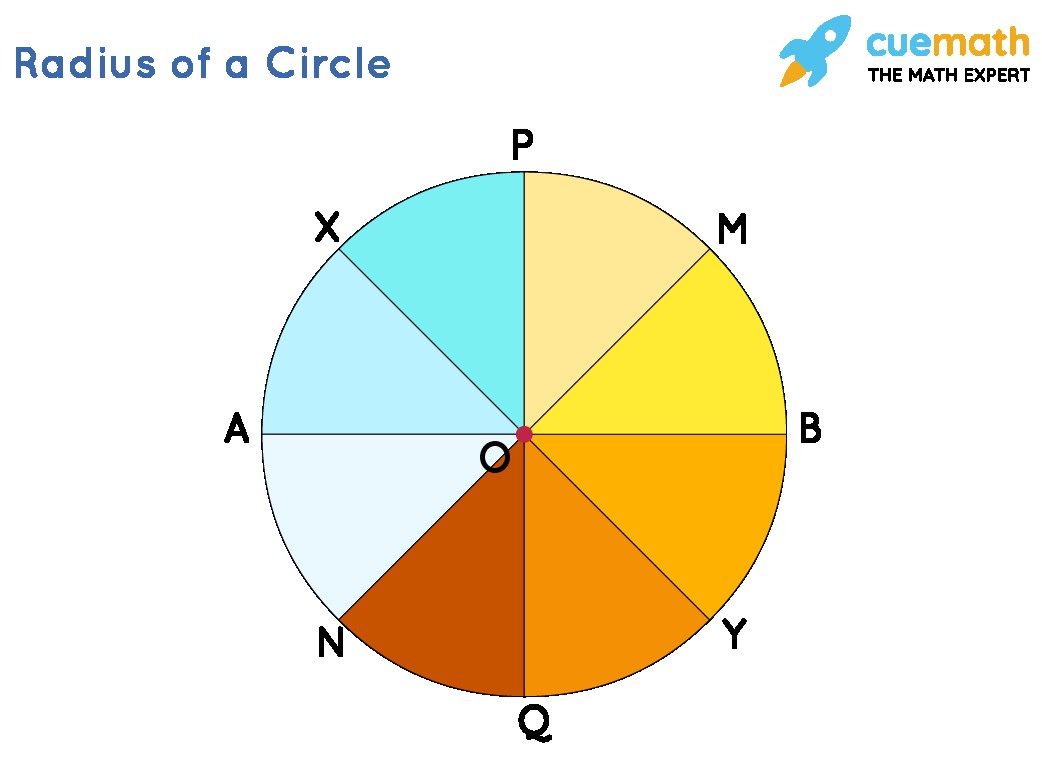
3.1. Infinite Radii, Equal Lengths
A circle can have an infinite number of radii, all originating from the center and extending to the circumference. A key property is that all these radii are equal in length. This is what defines a circle – all points on the circumference are equidistant from the center.
3.2. Radius and Circle Size
The length of the radius directly determines the size of the circle. A longer radius means a larger circle, with a greater circumference and area. Conversely, a shorter radius creates a smaller circle.
3.3. Visualizing the Radius
Imagine a compass, the tool used to draw circles. The fixed point of the compass represents the center of the circle, and the distance between the fixed point and the pencil tip represents the radius. As you rotate the compass, the pencil traces out the circumference, maintaining a constant distance (the radius) from the center.
3.4. Radii in Concentric Circles
Concentric circles are circles that share the same center but have different radii. Imagine a bullseye target; each ring represents a concentric circle with a different radius. The radii of these circles increase as you move outwards from the center.
4. How to Find the Radius of a Circle? Step-by-Step Guides
Let’s walk through how to find the radius using the formulas we discussed earlier:
4.1. Finding the Radius from the Diameter: A Simple Division
- Identify the diameter: This is the distance across the circle through the center.
- Divide by 2: Radius = Diameter / 2.
- Example: If the diameter of a circle is 10 cm, then the radius is 10 cm / 2 = 5 cm.
4.2. Finding the Radius from the Circumference: Using Pi
- Identify the circumference: This is the distance around the circle.
- Divide by 2π: Radius = Circumference / (2π). Remember that π is approximately 3.14159.
- Example: If the circumference of a circle is 25 inches, then the radius is 25 inches / (2 * 3.14159) ≈ 3.98 inches.
4.3. Finding the Radius from the Area: Square Root Required
- Identify the area: This is the amount of space inside the circle.
- Divide by π: Area / π.
- Take the square root: Radius = √(Area / π).
- Example: If the area of a circle is 50 square meters, then the radius is √(50 square meters / 3.14159) ≈ 3.99 meters.
4.4. Tips for Accurate Calculations
- Use a calculator: Especially when dealing with π, a calculator will give you a more precise answer.
- Pay attention to units: Make sure you’re using consistent units (e.g., all measurements in centimeters or all in inches).
- Double-check your work: It’s always a good idea to review your calculations to avoid errors.
5. Radius of Circle Equation: Diving into Coordinate Geometry
The radius plays a vital role in defining the equation of a circle in coordinate geometry.
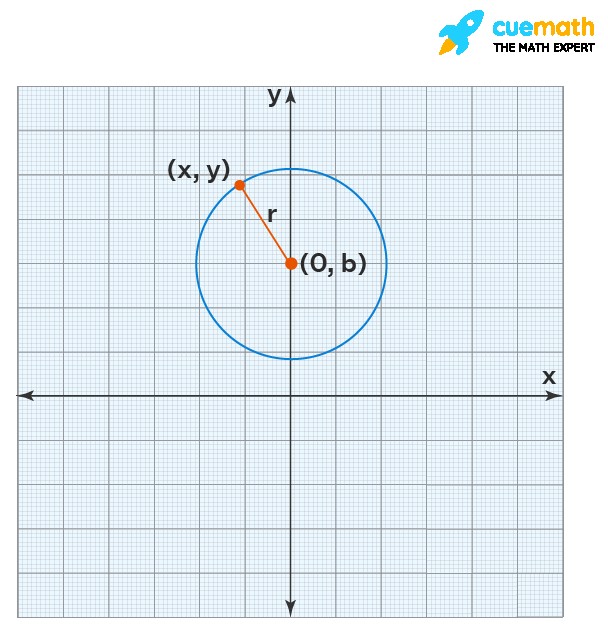
5.1. The Standard Equation of a Circle
In a Cartesian plane (x-y plane), the standard equation of a circle with center (h, k) and radius r is:
-
(x – h)² + (y – k)² = r²
This equation represents all the points (x, y) that lie on the circumference of the circle.
5.2. Understanding the Equation Components
- (x, y): Coordinates of any point on the circle’s circumference.
- (h, k): Coordinates of the center of the circle.
- r: The radius of the circle.
5.3. Finding the Radius from the Equation
If you’re given the equation of a circle, you can easily find the radius by:
-
Identifying the value of r²: This is the constant term on the right side of the equation.
-
Taking the square root: r = √(r²).
Example: If the equation of a circle is (x – 2)² + (y + 3)² = 16, then r² = 16, and the radius r = √16 = 4.
5.4. Circle Centered at the Origin
When the center of the circle is at the origin (0, 0), the equation simplifies to:
-
x² + y² = r²
This is a special case of the standard equation, where h = 0 and k = 0.
6. Radius of a Sphere: Extending the Concept to 3D
The concept of radius extends to three-dimensional objects, most notably the sphere.
6.1. Defining Radius in a Sphere
Just like in a circle, the radius of a sphere is the distance from the center of the sphere to any point on its surface.
6.2. Radius and Sphere Size
The radius of a sphere determines its size. A larger radius means a larger sphere, with a greater volume and surface area.
6.3. Calculating Volume and Surface Area with Radius
The radius is crucial for calculating the volume and surface area of a sphere:
- Volume (V) = (4/3)πr³
- Surface Area (A) = 4πr²
6.4. Finding the Radius from Volume or Surface Area
You can also calculate the radius of a sphere if you know its volume or surface area:
- Radius from Volume: r = ∛(3V / (4π)) (cube root)
- Radius from Surface Area: r = √(A / (4π))
7. FAQs on Radius: Your Questions Answered
Let’s address some frequently asked questions about the radius:
7.1. What is the Radius of a Circle in Geometry?
The radius of a circle is the distance from the center of the circle to any point on its circumference. It’s a fundamental property that defines the circle’s size and is used in various calculations.
7.2. How is Diameter Related to the Radius of the Circle?
The diameter of a circle is twice its radius. Diameter = 2 * Radius. Conversely, the radius is half the diameter.
7.3. How to Find the Radius from Circumference?
The formula to find the radius from the circumference is: Radius = Circumference / (2π), where π (pi) is approximately 3.14159.
7.4. What is the Radius Formula?
The radius formula depends on what information you have:
- From Diameter: Radius = Diameter / 2
- From Circumference: Radius = Circumference / (2π)
- From Area: Radius = √(Area / π)
7.5. How to Calculate Radius of Circle Using Calculator?
You can use a calculator to perform the divisions and square roots in the radius formulas. For example, when finding the radius from the circumference, divide the circumference by (2 * 3.14159).
7.6. How to Find the Radius of a Circle with the Area?
If you know the area of a circle, use the formula: Radius = √(Area / π). Divide the area by π and then take the square root of the result.
7.7. How to Calculate Radius from Diameter?
To calculate the radius from the diameter, simply divide the diameter by 2: Radius = Diameter / 2.
Unlock Your Knowledge Potential with WHAT.EDU.VN
Are you still struggling with the radius or other geometry concepts? Do you have questions that need answers? Don’t waste time searching endlessly – visit WHAT.EDU.VN today and ask your questions for free!
At WHAT.EDU.VN, we provide a platform where you can connect with experts and receive quick, accurate, and easy-to-understand answers to all your questions. Whether you’re a student, a professional, or simply curious, our community is here to help.
Here’s how WHAT.EDU.VN can help you:
- Ask any question, no matter how simple or complex.
- Get answers from knowledgeable experts.
- Receive fast and reliable information.
- Access a user-friendly platform for easy question submission.
- Enjoy free consultation services for basic inquiries.
Stop feeling frustrated by unanswered questions. Join WHAT.EDU.VN and experience the power of collaborative learning. Our address is 888 Question City Plaza, Seattle, WA 98101, United States. Contact us on WhatsApp at +1 (206) 555-7890, or visit our website at WHAT.EDU.VN.
Don’t hesitate – your answers await!
Let what.edu.vn be your trusted source for knowledge and support. We’re committed to providing you with the information you need to succeed.
