What Is The Area Of The Circle? Find out on WHAT.EDU.VN! Unlock the secrets of circle geometry with our comprehensive guide. Discover formulas, examples, and real-world applications. Master circle area calculations today and ask any question for free!
1. Introduction to Circle Area
The area of a circle is the measurement of the two-dimensional space enclosed within its circumference. This is a fundamental concept in geometry with wide-ranging applications in various fields. Understanding how to calculate the area of a circle is essential for students, professionals, and anyone curious about the world around them. The area can be found using different parameters of the circle, such as radius, diameter, or circumference. Do you have questions about area calculation? Ask WHAT.EDU.VN for a free answer!
2. Understanding the Definition of Circle Area
2.1. Defining Circle Area
The area of a circle refers to the region enclosed within its boundary, often referred to as its circumference. It quantifies the total amount of space contained within the circle’s perimeter. The area of a circle is expressed in square units, such as square meters (m²), square centimeters (cm²), or square inches (in²), reflecting its two-dimensional nature. Whether you’re dealing with small circles or large ones, the area represents the amount of surface it covers. Need help with a specific area calculation? WHAT.EDU.VN can provide clear, concise answers.
2.2. Formula for Calculating Circle Area
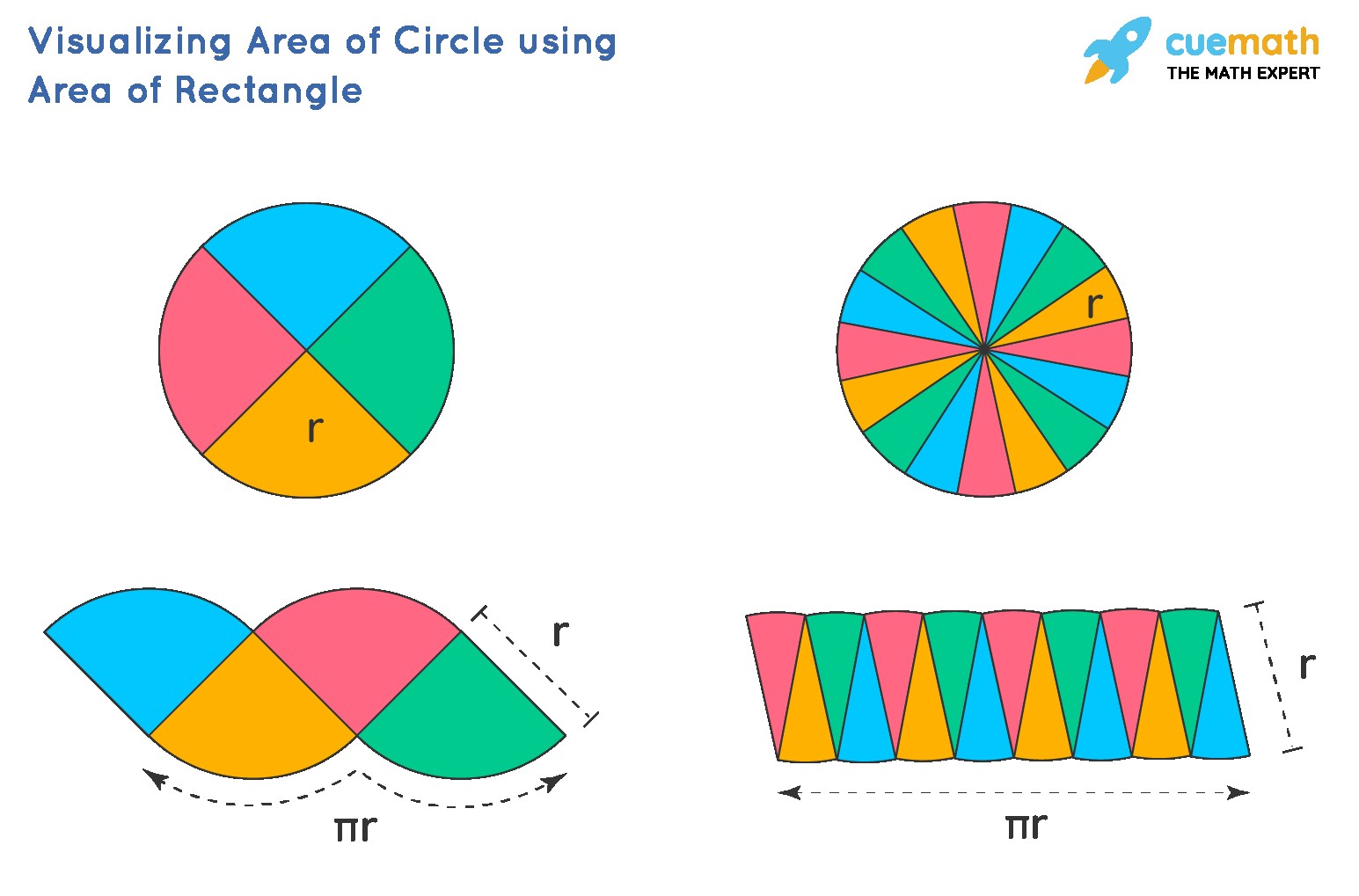
The most common formula for finding the area of a circle is:
A = πr²
Where:
- A represents the area of the circle.
- π (pi) is a mathematical constant approximately equal to 3.14159.
- r is the radius of the circle, which is the distance from the center of the circle to any point on its circumference.
2.3. Understanding the Symbol π (pi)
Pi (π) is a fundamental constant in mathematics that represents the ratio of a circle’s circumference to its diameter. Its value is approximately 3.14159, but it is an irrational number, meaning its decimal representation goes on infinitely without repeating. Pi is used extensively in calculations involving circles, including finding the area, circumference, and volume of related shapes. Pi represents the circle constant. Still puzzled by pi? Get clarification on WHAT.EDU.VN without any cost!
2.4. Role of the Radius in Circle Area Calculation
The radius plays a critical role in determining the area of a circle. Because the radius is squared in the formula (A = πr²), even small changes in the radius can significantly affect the area. A larger radius results in a proportionally larger area, and vice versa. If you have the diameter, you can easily find the radius by dividing it by two (r = d/2). Remember, accuracy in measuring the radius is crucial for accurate area calculations.
3. Exploring Circle Components
3.1. Radius of a Circle
The radius of a circle is the distance from its center to any point on its circumference. It is a fundamental measurement used in many circle-related calculations. The radius is half the length of the diameter, which is the distance across the circle passing through its center. Knowing the radius allows you to calculate the area, circumference, and other properties of the circle. Do you struggle with identifying the radius? Ask for free help on WHAT.EDU.VN.
3.2. Diameter of a Circle
The diameter of a circle is the distance across the circle, passing through its center. It is twice the length of the radius. The diameter is useful for calculating the circumference and area of a circle, especially when the radius is not directly given. Understanding the relationship between the diameter and radius is essential for solving circle-related problems. The diameter helps in area determination.
3.3. Circumference of a Circle
The circumference of a circle is the distance around its boundary. It is also known as the perimeter of the circle. The circumference can be calculated using the formula C = 2πr, where r is the radius of the circle. Knowing the circumference can help you determine the radius and, consequently, the area of the circle. The circumference measures the boundary.
3.4. Center of a Circle
The center of a circle is the point equidistant from all points on its circumference. It is the reference point from which the radius is measured. The center is crucial for defining the circle and performing geometric constructions. Locating the center accurately is essential for precise calculations of the circle’s properties. Have more questions? Get answers on WHAT.EDU.VN easily!
4. Detailed Formulas for Circle Area Calculation
4.1. Area Formula Using Radius
The most fundamental formula for calculating the area of a circle is:
A = πr²
Where:
- A is the area of the circle.
- π (pi) is approximately 3.14159.
- r is the radius of the circle.
This formula is straightforward and widely used when the radius of the circle is known. The area is directly proportional to the square of the radius, meaning that if you double the radius, the area increases by a factor of four. Understanding the impact of radius on the overall area is crucial.
4.2. Area Formula Using Diameter
When the diameter (d) of the circle is known instead of the radius, you can use the following formula to find the area:
A = π(d/2)² = (π/4)d²
Where:
- A is the area of the circle.
- π (pi) is approximately 3.14159.
- d is the diameter of the circle.
This formula is derived from the fact that the radius is half the diameter (r = d/2). Substituting this relationship into the basic area formula (A = πr²) gives you the formula in terms of the diameter. Using the diameter can simplify calculations in certain situations.
4.3. Area Formula Using Circumference
If you know the circumference (C) of the circle, you can calculate the area using the following formula:
A = C² / (4π)
Where:
- A is the area of the circle.
- C is the circumference of the circle.
- π (pi) is approximately 3.14159.
This formula is derived from the relationship between the circumference and the radius (C = 2πr). Solving for the radius (r = C / (2π)) and substituting it into the basic area formula (A = πr²) gives you the formula in terms of the circumference. Using the circumference is particularly useful when the radius or diameter is not directly provided.
5. Step-by-Step Guide to Calculating Circle Area
5.1. Identify Given Information
The first step in calculating the area of a circle is to identify the information you have. This could be the radius, diameter, or circumference. Knowing what you have will determine which formula to use. Make sure the units are consistent; if the radius is in centimeters, the area will be in square centimeters. Are you unsure which information you have? Ask WHAT.EDU.VN for guidance.
5.2. Select the Appropriate Formula
Once you know the given information, choose the appropriate formula:
- If you have the radius (r), use: A = πr²
- If you have the diameter (d), use: A = (π/4)d²
- If you have the circumference (C), use: A = C² / (4π)
Choosing the correct formula is crucial for accurate calculations.
5.3. Substitute Values into the Formula
Next, substitute the known values into the chosen formula. Be careful to substitute correctly and ensure that you are using the proper units. For example, if the radius is 5 cm, the formula A = πr² becomes A = π(5 cm)². Substitute correctly to avoid errors.
5.4. Perform the Calculation
After substituting the values, perform the calculation. Remember to follow the order of operations (PEMDAS/BODMAS). This usually involves squaring the radius or diameter first, then multiplying by π (approximately 3.14159). If you find calculations daunting, WHAT.EDU.VN is here to help.
5.5. State the Answer with Correct Units
Finally, state the answer with the correct units. Since area is a measure of two-dimensional space, the units will be square units, such as square meters (m²), square centimeters (cm²), or square inches (in²). Always include the units to provide a complete and meaningful answer.
6. Real-World Examples of Circle Area Calculation
6.1. Calculating the Area of a Circular Garden
Imagine you have a circular garden with a radius of 8 meters. To find the area of the garden, you would use the formula A = πr². Substituting the radius, you get A = π(8 m)² = π(64 m²) ≈ 201.06 m². Thus, the area of the circular garden is approximately 201.06 square meters. Applying the formula to real scenarios helps solidify the concept.
6.2. Determining the Size of a Pizza
Suppose you want to know the area of a pizza with a diameter of 12 inches. Using the formula A = (π/4)d², you get A = (π/4)(12 in)² = (π/4)(144 in²) ≈ 113.10 in². Therefore, the area of the pizza is approximately 113.10 square inches. You can use this information to compare the sizes of different pizzas.
6.3. Finding the Area of a Circular Tabletop
If you have a circular tabletop with a circumference of 150 cm, you can find its area using the formula A = C² / (4π). Substituting the circumference, you get A = (150 cm)² / (4π) = 22500 cm² / (4π) ≈ 1790.49 cm². This means the area of the tabletop is approximately 1790.49 square centimeters.
6.4. Area Calculations in Engineering
Engineers often need to calculate the area of circular components in various designs. For example, when designing a circular pipe with a radius of 0.5 meters, the area can be calculated as A = πr² = π(0.5 m)² = π(0.25 m²) ≈ 0.785 m². This calculation is crucial for determining the flow capacity of the pipe. Engineering demands precise area calculations.
7. Common Mistakes to Avoid
7.1. Using Diameter Instead of Radius
A common mistake is using the diameter directly in the area formula A = πr² without dividing it by 2 to get the radius. Remember, the formula requires the radius, so always convert the diameter to the radius before calculating the area. Failing to convert leads to calculation errors.
7.2. Forgetting to Square the Radius
Another frequent mistake is forgetting to square the radius in the formula A = πr². The radius must be squared before multiplying by π. This is a crucial step, as squaring the radius has a significant impact on the final area.
7.3. Incorrectly Approximating Pi (π)
While using 3.14 as an approximation for π is common, it can lead to inaccuracies, especially in precise calculations. Using a more accurate value of π, such as 3.14159, or using the π button on a calculator, can improve the accuracy of your results. Accuracy in pi approximation matters.
7.4. Not Including Units in the Final Answer
Forgetting to include the correct units in the final answer is a common oversight. Always remember to express the area in square units, such as square meters (m²) or square centimeters (cm²). Including units provides context and completes the answer.
8. Advanced Applications of Circle Area
8.1. Calculating the Area of a Sector
A sector is a portion of a circle enclosed by two radii and an arc. To find the area of a sector, you can use the formula:
Area of Sector = (θ / 360°) × πr²
Where:
- θ is the central angle of the sector in degrees.
- r is the radius of the circle.
Understanding sectors is essential for advanced geometrical problems.
8.2. Finding the Area of a Circular Segment
A segment is a region of a circle bounded by an arc and a chord. The area of a segment can be found by subtracting the area of the triangle formed by the chord and the center from the area of the sector. The formula is:
Area of Segment = Area of Sector – Area of Triangle
Calculating segments is important in architectural and engineering contexts.
8.3. Applications in Calculus
In calculus, the area of a circle can be calculated using integration. The equation of a circle centered at the origin is x² + y² = r². By integrating over the appropriate limits, you can derive the area formula A = πr². Calculus provides a rigorous method for area determination.
8.4. Circle Areas in 3D Geometry
Understanding circle areas is crucial in calculating the surface areas and volumes of 3D shapes like spheres, cylinders, and cones. For example, the surface area of a sphere is 4πr², which directly uses the concept of circle area. Connecting circles to 3D shapes enhances problem-solving skills.
9. Optimizing Circle Area for Different Scenarios
9.1. Maximizing Area with Fixed Perimeter
Given a fixed perimeter (circumference), the shape that maximizes the enclosed area is a circle. This principle is used in various applications, such as designing enclosures that need to maximize space within a given boundary. Circles are optimal for maximum area.
9.2. Minimizing Perimeter for Fixed Area
Conversely, given a fixed area, the shape that minimizes the perimeter is a circle. This is useful in scenarios where you want to use the least amount of material to enclose a specific area, such as in packaging design. Circles minimize perimeter usage.
9.3. Efficient Design in Engineering
In engineering, circular shapes are often used because they provide structural efficiency and maximize area or volume while minimizing material usage. Examples include pipes, tanks, and pressure vessels, where circular designs offer optimal performance. Engineering designs benefit from circular efficiency.
9.4. Space Planning in Architecture
Architects use circle area calculations to optimize space in buildings and landscapes. Circular layouts can create unique designs while maximizing usable area. Understanding circle area helps in innovative architectural designs.
10. Practice Problems for Circle Area Calculation
10.1. Problem 1: Finding Area Given Radius
A circle has a radius of 7 cm. Calculate its area.
Solution:
Using the formula A = πr², A = π(7 cm)² = π(49 cm²) ≈ 153.94 cm². The area is approximately 153.94 square centimeters.
10.2. Problem 2: Finding Area Given Diameter
A circle has a diameter of 10 inches. Calculate its area.
Solution:
Using the formula A = (π/4)d², A = (π/4)(10 in)² = (π/4)(100 in²) ≈ 78.54 in². The area is approximately 78.54 square inches.
10.3. Problem 3: Finding Area Given Circumference
A circle has a circumference of 25 meters. Calculate its area.
Solution:
Using the formula A = C² / (4π), A = (25 m)² / (4π) = 625 m² / (4π) ≈ 49.74 m². The area is approximately 49.74 square meters.
10.4. Problem 4: Sector Area Calculation
A sector of a circle has a radius of 6 cm and a central angle of 60 degrees. Calculate its area.
Solution:
Using the formula Area of Sector = (θ / 360°) × πr², Area = (60° / 360°) × π(6 cm)² = (1/6) × π(36 cm²) ≈ 18.85 cm². The sector area is approximately 18.85 square centimeters.
11. Tips for Mastering Circle Area Calculations
11.1. Memorize the Formulas
Memorizing the area formulas for circles (A = πr², A = (π/4)d², A = C² / (4π)) is crucial for quick and accurate calculations. Flashcards and regular practice can help reinforce these formulas.
11.2. Practice Regularly
Consistent practice is key to mastering circle area calculations. Solve a variety of problems involving different given information (radius, diameter, circumference) to build confidence and proficiency.
11.3. Understand the Concepts
Focus on understanding the underlying concepts rather than just memorizing formulas. Knowing why the formulas work will help you apply them correctly in different situations. Conceptual understanding enhances problem-solving.
11.4. Use Online Resources
Take advantage of online resources such as calculators, tutorials, and practice problems to enhance your learning. Websites like WHAT.EDU.VN offer free answers and guidance to help you grasp the concepts.
12. Why Use WHAT.EDU.VN for Your Questions?
12.1. Free Answers
WHAT.EDU.VN provides free answers to all your questions, making learning accessible to everyone. You can ask any question about circle area calculations and receive prompt, accurate responses without any cost.
12.2. Expert Explanations
Our team of experts provides detailed explanations to help you understand the concepts thoroughly. You can rely on us for accurate and clear guidance, ensuring that you grasp the nuances of circle area calculations.
12.3. Convenient Access
Accessing our services is easy and convenient. Simply visit WHAT.EDU.VN, ask your question, and receive a timely response. Our platform is designed to provide quick and reliable support whenever you need it.
12.4. Comprehensive Coverage
Whether you have questions about basic formulas or advanced applications, WHAT.EDU.VN offers comprehensive coverage of all topics related to circle area. You can find answers to a wide range of questions, ensuring that you get the support you need for all your learning endeavors.
13. Test Your Knowledge: Quiz on Circle Area
13.1. Question 1
What is the area of a circle with a radius of 9 cm?
- A) 28.27 cm²
- B) 56.55 cm²
- C) 254.47 cm²
- D) 153.94 cm²
13.2. Question 2
What is the area of a circle with a diameter of 14 inches?
- A) 615.75 in²
- B) 153.94 in²
- C) 43.98 in²
- D) 153.86 in²
13.3. Question 3
What is the area of a circle with a circumference of 30 meters?
- A) 71.62 m²
- B) 28.65 m²
- C) 22.5 m²
- D) 107.44 m²
13.4. Question 4
A sector of a circle has a radius of 8 cm and a central angle of 45 degrees. Calculate its area.
- A) 25.13 cm²
- B) 50.27 cm²
- C) 12.57 cm²
- D) 100.53 cm²
14. Advanced Problem Solving
14.1. Problem: Area of an Annulus
An annulus is the region between two concentric circles. If the outer radius is R and the inner radius is r, the area of the annulus is A = π(R² – r²). Calculate the area of an annulus where R = 10 cm and r = 6 cm.
Solution:
A = π(10² – 6²) = π(100 – 36) = π(64) ≈ 201.06 cm².
14.2. Problem: Combining Circles
Two circles have radii of 3 cm and 4 cm. What is the radius of a circle whose area is equal to the sum of the areas of these two circles?
Solution:
Area of circle 1: A₁ = π(3²) = 9π cm²
Area of circle 2: A₂ = π(4²) = 16π cm²
Total area: A = A₁ + A₂ = 9π + 16π = 25π cm²
Radius of combined circle: r = √(A/π) = √(25π/π) = √25 = 5 cm.
14.3. Problem: Circle Inscribed in a Square
A circle is inscribed in a square of side length 8 cm. Find the area of the circle.
Solution:
The diameter of the circle is equal to the side length of the square, so d = 8 cm. The radius is r = d/2 = 4 cm. The area of the circle is A = πr² = π(4²) = 16π ≈ 50.27 cm².
14.4. Problem: Percentage Increase in Area
If the radius of a circle is increased by 20%, by what percentage does the area increase?
Solution:
Let the original radius be r. The new radius is 1.2r.
Original area: A₁ = πr²
New area: A₂ = π(1.2r)² = π(1.44r²) = 1.44πr²
Percentage increase: ((A₂ – A₁) / A₁) × 100% = ((1.44πr² – πr²) / πr²) × 100% = (0.44) × 100% = 44%.
15. Practical Tools and Resources
15.1. Online Circle Area Calculators
Numerous online calculators are available to quickly compute the area of a circle given the radius, diameter, or circumference. These tools can be valuable for checking your work and saving time.
15.2. Geometry Software
Software like GeoGebra and AutoCAD allow you to create and analyze circles and other geometric shapes. These tools can help you visualize concepts and perform complex calculations.
15.3. Mobile Apps
Many mobile apps are designed to help with geometry calculations. These apps can be useful for students and professionals who need to perform calculations on the go.
15.4. Educational Websites
Websites like Khan Academy and Cuemath offer comprehensive lessons and practice problems on circle area and related topics. These resources can supplement your learning and provide additional support.
16. Call to Action: Ask Your Questions on WHAT.EDU.VN
Still have questions about circle area? Don’t hesitate! Visit WHAT.EDU.VN today and ask your questions for free. Our experts are ready to provide detailed explanations and guidance to help you master circle area calculations. Whether you’re struggling with a specific problem or want to deepen your understanding, WHAT.EDU.VN is here to support you.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Take the next step in your learning journey and unlock the secrets of circle area with WHAT.EDU.VN! We are committed to providing accessible, high-quality education to learners of all ages and backgrounds. Join our community and experience the difference that expert guidance can make. We’re here to help you succeed!
17. FAQ: Area of a Circle
17.1. What is the area of a circle?
The area of a circle is the measure of the two-dimensional space enclosed within the circumference of the circle. It is calculated using the formula A = πr², where r is the radius of the circle.
17.2. How do I calculate the area of a circle if I only know the diameter?
If you know the diameter (d), you can calculate the area using the formula A = (π/4)d². Remember that the diameter is twice the radius, so d = 2r.
17.3. How do I calculate the area of a circle if I only know the circumference?
If you know the circumference (C), you can calculate the area using the formula A = C² / (4π). This formula is derived from the relationship C = 2πr.
17.4. What is the value of pi (π)?
Pi (π) is a mathematical constant approximately equal to 3.14159. It is the ratio of a circle’s circumference to its diameter.
17.5. Why is it important to include units when stating the area of a circle?
Including units is important because area is a measure of two-dimensional space. The units indicate the scale of the measurement (e.g., square meters, square centimeters, square inches).
17.6. How does the area of a circle change if the radius is doubled?
If the radius of a circle is doubled, the area increases by a factor of four. This is because the area formula is A = πr², so if r is replaced with 2r, the new area is A = π(2r)² = 4πr².
17.7. What is a sector of a circle?
A sector of a circle is a portion of the circle enclosed by two radii and an arc. The area of a sector can be calculated using the formula Area of Sector = (θ / 360°) × πr², where θ is the central angle of the sector in degrees.
17.8. Can the area of a circle be negative?
No, the area of a circle cannot be negative. Area is a measure of space and is always a non-negative value.
17.9. How accurate do I need to be when using the value of pi (π) to calculate the area?
The accuracy required depends on the specific application. For most practical purposes, using 3.14 or 3.14159 is sufficient. However, for very precise calculations, you may need to use more digits of pi.
17.10. Where can I find more help with circle area calculations?
You can find more help with circle area calculations on websites like what.edu.vn, Khan Academy, and Cuemath. These resources offer lessons, practice problems, and expert explanations to support your learning.