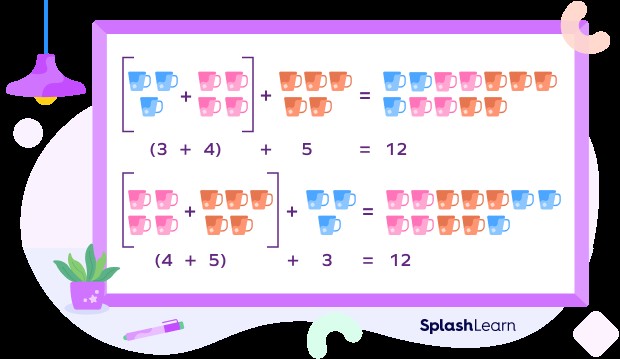
The associative property is a fundamental concept in mathematics that simplifies calculations. It states that when adding or multiplying three or more numbers, the way they are grouped does not affect the final result. This guide will delve into the associative property, providing clear definitions, examples, and addressing common questions.
The associative property states that when you add or multiply three or more numbers, changing the grouping of the numbers does not change the result. The key takeaway is that the order of the numbers remains the same, only the parentheses (grouping) changes.
For example:
2 × (7 × 6) = (2 × 7) × 6
2 + (7 + 6) = (2 + 7) + 6
Associative Property of Addition
The associative property of addition means you can add numbers in any grouping without changing the sum. Mathematically, this is expressed as:
(x + y) + z = x + (y + z)
This formula shows that whether you add x and y first, and then z, or add y and z first, and then x, the final answer will be the same.
Associative Property of Multiplication
Similarly, the associative property of multiplication states that the product remains the same regardless of how the numbers are grouped. The mathematical expression is:
(p × q) × r = p × (q × r)
This means you can multiply p and q first, then multiply by r, or you can multiply q and r first, and then multiply by p. Either way, the final product will be identical.
Associative Property vs. Commutative Property
It’s important to distinguish the associative property from the commutative property.
Commutative Property
The commutative property says that changing the order of numbers being added or multiplied doesn’t change the result. For addition: a + b = b + a. For multiplication: a × b = b × a.
The main difference between the associative and commutative properties is the number of terms involved. The commutative property deals with two numbers, while the associative property deals with three or more numbers. The commutative property changes the order, while the associative property changes the grouping.
Applicability to Division and Subtraction
The associative property does not apply to subtraction and division. Let’s look at examples:
Subtraction:
12 – (6 – 2) = 12 – 4 = 8
(12 – 6) – 2 = 6 – 2 = 4
Therefore, 12 – (6 – 2) ≠ (12 – 6) – 2
Division:
(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3
24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12
Therefore, (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2)
These examples demonstrate that changing the grouping in subtraction and division problems does affect the result, meaning the associative property is not applicable.
Fun Fact!
The associative property’s name comes from the word “associate,” which refers to how numbers are grouped together.
Solved Examples of the Associative Property
Example 1: If (30 × 20) × 15 = 9000, find (15 × 30) × 20 using the associative property.
Solution: According to the associative property of multiplication, the grouping doesn’t change the result: (30 × 20) × 15 = (15 × 30) × 20.
Therefore, since (30 × 20) × 15 = 9000, then (15 × 30) × 20 = 9000.
Example 2: Determine if the associative property of addition applies to the following equations:
- 20 + (60 + 5) = (20 + 60) + 5
- 30 + (40 + 20) = (30 + 10) + 50
Solution:
-
Let’s evaluate both sides of the equation:
LHS: 20 + (60 + 5) = 20 + 65 = 85
RHS: (20 + 60) + 5 = 80 + 5 = 85
LHS = RHS. Therefore, the associative property of addition is demonstrated in this equation.
-
Let’s evaluate both sides of the equation:
LHS: 30 + (40 + 20) = 30 + 60 = 90
RHS: (30 + 10) + 50 = 40 + 50 = 90
LHS = RHS. Although both sides are equal, this equation does not demonstrate the associative property because the numbers have been changed on either side of the equation, violating the rule that only the grouping can change.
Example 3: Fill in the missing number according to the associative property:
(5 + 10) + 4 = (5 + 4) + __ = 19
Solution: According to the associative property, the grouping of numbers does not affect the sum. Therefore, (5 + 10) + 4 = (5 + 4) + 10 = 19
Practice Problems
Test your understanding with these practice questions:
-
Complete the following equation: 2 × (__ × 6) = (2 × 5) × __
-
Fill in the blanks: 20 + 9 + __ = 9 + 5 + __
-
Which of these equations is correct?
- (2 + 3) + 6 = 2 × (3 + 6)
- (5 + 6) + 4 = 5 + (6 + 4)
- (7 – 10) – 15 = 7 – (10 – 15)
- (9 ÷ 3) ÷ 3 = 9 ÷ (3 ÷ 3)
Frequently Asked Questions (FAQs)
For how many numbers can the associative property of addition and multiplication be used?
The associative property of addition and multiplication applies to three or more numbers.
Does the associative property apply to fractions?
Yes, the associative property of addition and multiplication holds true for fractions.
Does the associative property apply to an equation that includes 0?
Yes, the associative property holds true for equations including 0.