Are you curious about the constant of proportionality and how it helps us understand relationships between quantities? At WHAT.EDU.VN, we simplify complex concepts, offering clear explanations and practical examples. Discover how this fundamental idea unlocks a deeper understanding of direct and inverse variation, offering you a new perspective. Let’s explore proportionality constant, proportionality factor, and unit rate, and remember, if you have more questions, WHAT.EDU.VN is here to help for free.
1. What is the Constant of Proportionality?
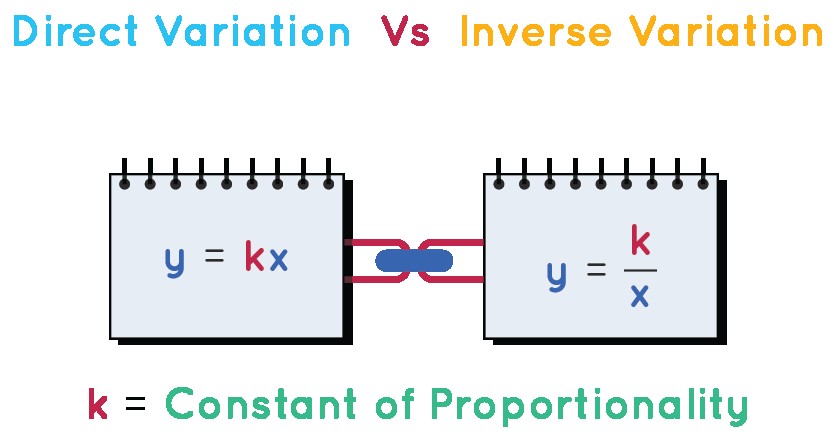
The constant of proportionality is a constant value representing the ratio between two proportional quantities. When two variables are in direct or inverse proportion, their relationship can be expressed as y = kx or y = k/x, where k is the constant of proportionality. This value, k, defines how the two quantities are related.
- Direct Variation: In direct proportionality, the equation is y = kx. As x increases, y increases proportionally.
- Example: The total cost (y) is directly proportional to the number of items (x) purchased, denoted as y ∝ x.
- Inverse Variation: In inverse proportionality, the equation is y = k/x. As x increases, y decreases, and vice versa.
- Example: The speed of a vehicle (y) is inversely proportional to the time (x) taken to cover a certain distance, denoted as y ∝ 1/x.
In both scenarios, k remains constant. This constant value is referred to as the constant of proportionality or the unit rate.
Alt text: Visual representation illustrating constant of proportionality in both direct and inverse variation scenarios.
2. Why Do We Use the Constant of Proportionality?
The constant of proportionality is used to determine the rate of change between two variables and to identify whether the relationship is a direct or inverse variation. For instance, if two apples cost $20, we can find that one apple costs $10. Here, $10 is the constant of proportionality for the cost of an apple.
Imagine drawing a picture of the Taj Mahal. To accurately represent the monument on paper, you must maintain a proportional relationship between the lengths, heights, and widths of the building. The constant of proportionality helps you scale the measurements to achieve the desired outcome. For example, if the dome’s height is 2 meters, you can represent it as 2 inches in your drawing.
Working with proportional relationships is essential for solving many real-world problems:
- Adjusting ingredient ratios in a recipe.
- Quantifying probabilities and odds of events.
- Scaling diagrams for architecture and drafting.
- Calculating percentage increases or decreases for price markups.
- Determining discounts on products based on the unit rate.
3. How to Solve for the Constant of Proportionality?
Solving for the constant of proportionality involves identifying whether the relationship is a direct or inverse variation and then applying the appropriate formula.
Example 1: If y = 24 and x = 3, and y ∝ x, find the constant of proportionality.
- Since y varies proportionally with x, we write the equation as y = kx.
- Substitute the given values: 24 = k(3).
- Solve for k: k = 24 ÷ 3 = 8.
- Therefore, the constant of proportionality is 8.
Example 2: Four workers take 3 hours to complete a task. If two more workers are hired, how long will it take them to complete the same task?
- Let x1 = number of workers in case 1 = 4.
- Let x2 = number of workers in case 2 = 6.
- Let y1 = number of hours in case 1 = 3.
- Let y2 = number of hours in case 2 = Unknown.
Since more workers will reduce the time needed, the number of workers is inversely proportional to the time taken.
- y1 = k/x1 => 3 = k/4 => k = 12.
- To find the number of hours with six workers: y2 = k/x2 => y2 = 12/6 = 2 hours.
4. Identifying the Constant of Proportionality
Identifying the constant of proportionality involves recognizing the relationship between variables in tables or graphs.
Examine the table below to determine if the relationship is proportional and find the constant of proportionality.
| Number of Days (x) | 1 | 3 | 5 | 6 |
|---|---|---|---|---|
| Number of Articles (y) | 3 | 9 | 15 | 18 |

As the number of days increases, the number of articles written also increases, indicating a direct proportion. We use the equation y = kx to find the constant of proportionality, which is k = y/x.
- y/x = 3/1 = 9/3 = 15/5 = 18/6 = 3
Since the ratio of y to x is consistently 3, the constant of proportionality is 3.
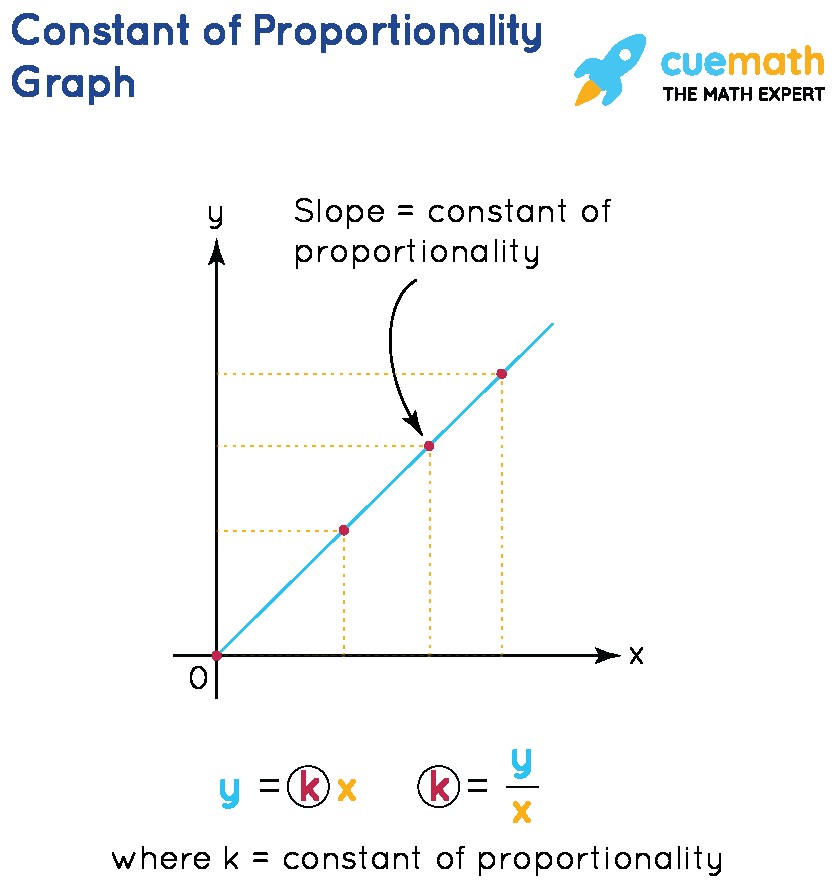
When plotting these values on a graph, a straight line passing through the origin indicates a proportional relationship. The constant of proportionality in a direct proportion is the slope of this line.
Alt text: A graph illustrating direct proportionality with a straight line passing through the origin.
5. Solved Examples
Let’s explore more examples to solidify our understanding.
-
Example 1: Examine the table below. Do the variables exhibit any type of proportion? If so, What Is The Constant Of Proportionality?
X Y 5 1 25 5 16 3 35 7 To check for proportionality, use y = kx, or k = y/x.
- y/x = 1/5 = 5/25 = 7/35 ≠ 3/16
Since the ratios are not equal, these values are not in a proportional relationship.
-
Example 2: Assume y varies directly with x, and y = 30 when x = 6. Use the constant of proportionality to find the value of y when x = 100.
Write the equation: y = kx. Substitute the given values to solve for k.
- 30 = k × 6 => k = 5
The equation is now y = 5x. Substitute x = 100 to find y.
- y = 5 × 100 = 500
Therefore, y = 500 when x = 100.
-
Example 3: Anthony takes 15 days to reduce 30 kilograms of weight by exercising 30 minutes per day. If he exercises for 1 hour and 30 minutes every day, how many days will he take to reduce the same weight?
Weight and exercise time are inversely proportional. As exercise time increases, the number of days decreases. Let m be minutes and d be days. Then, m = k/d. We have m1 = 30, m2 = 90, d1 = 15, and we need to find d2.
- m1 = k/d1 => k = 30 × 15 = 450
- m2 = k/d2 => 90 = 450/d2 => d2 = 450/90 = 5
Therefore, if Anthony exercises for 1 hour and 30 minutes per day, it will take him only 5 days to reduce 30 kilograms.
Alt text: A child enthusiastically learning math concepts on a laptop.
6. Practice Questions
Test your understanding with these practice questions.
- If a is directly proportional to b, and a = 12 when b = 4, find a when b = 7.
- Suppose x and y are inversely proportional, and x = 5 when y = 10. Find y when x = 2.
- A recipe requires 2 cups of flour for every 3 cups of sugar. What is the constant of proportionality relating flour to sugar?
- If 5 workers can complete a project in 8 days, how many days will it take 10 workers, assuming they work at the same rate?
7. FAQs on the Constant of Proportionality
Let’s address some frequently asked questions about the constant of proportionality.
7.1 What is Another Name for the Constant of Proportionality?
Another name for the constant of proportionality is the unit rate. It represents the constant ratio between two proportional quantities.
7.2 What is the Constant of Proportionality in a Graph?
In a graph, the constant of proportionality is represented by the slope of a straight line that passes through the origin. This line illustrates the proportional relationship between two variables.
7.3 Why Do We Use the Constant of Proportionality?
The constant of proportionality helps determine the nature of proportionality (direct or inverse) and solve equations involving ratios and proportions. It provides a clear and consistent way to relate two quantities.
7.4 What is the Constant of Proportionality of 12/6?
To find the constant of proportionality in the case of direct proportionality, use k = y/x. If y = 12 and x = 6, then k = 12/6 = 2.
7.5 What is the Constant of Proportionality?
If the ratio of one variable to another is constant, the two variables have a proportional relationship. If x and y have a proportional relationship, the constant of proportionality is the ratio of y to x. This can also be represented as x is to y.
Still have questions about the constant of proportionality? Don’t hesitate to ask for free on WHAT.EDU.VN. We’re here to provide you with clear, concise answers to all your academic questions.
We understand that finding answers to your questions can be challenging. You might not know who to ask, or you might worry about the cost of getting help. At WHAT.EDU.VN, we believe everyone deserves access to quick, accurate, and free information.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t struggle alone. Visit what.edu.vn today and get the answers you need, absolutely free.