Are you curious about circles and their measurements? WHAT.EDU.VN is here to help you understand everything about the diameter of a circle, offering clear explanations and easy-to-use resources. Discover how to calculate the diameter and its significance with us, while exploring circle dimensions and essential geometric concepts.
1. Understanding the Diameter of a Circle
The diameter of a circle is a fundamental concept in geometry. It is defined as any straight line segment that passes through the center of the circle, with both endpoints lying on the circle’s circumference. In simpler terms, it’s the longest possible distance across a circle. This line divides the circle into two equal halves.
1.1. Definition of Diameter
The diameter is exactly twice the length of the radius of a circle. The radius measures the distance from the center of the circle to any point on its edge, while the diameter stretches from one edge to the opposite edge, passing through the center. It’s typically denoted by the letter ‘D’. A circle has countless diameters, all equal in length, each cutting the circle precisely in half.
1.2. Diameter Symbol
In engineering, the symbol “⌀” is used to represent diameter. This symbol, often called “phi,” is commonly found in technical drawings and specifications. For example, “⌀50 mm” indicates that the diameter of the circle is 50 millimeters.
2. Essential Formulas for the Diameter of a Circle
Understanding the different formulas helps in various calculations involving circles. Before delving into the formulas, let’s define key terms:
- Radius (r): The distance from the center of the circle to any point on its circumference.
- Circumference (C): The distance around the circle.
- Area (A): The space enclosed within the circle.
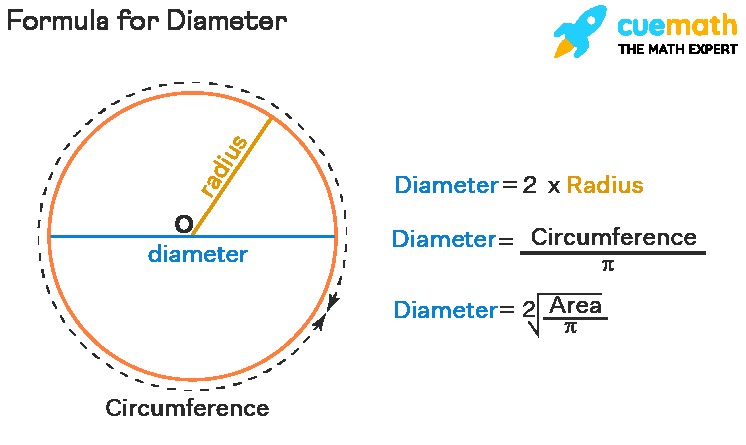Diameter Formula
2.1. Diameter Calculation Using Circumference
The circumference of a circle is calculated using the formula C = πd, where ‘d’ is the diameter and π (pi) is approximately 3.14159. From this, the formula to find the diameter is:
Diameter = Circumference / π
2.2. Diameter Calculation Using Radius
The most straightforward way to find the diameter is by using the radius. Since the diameter is twice the radius, the formula is:
Diameter = 2 × Radius
2.3. Diameter Calculation Using Area
The area of a circle is given by the formula A = πr². To find the diameter using the area, we rearrange the formula to solve for the radius first:
r = √(A / π)
Then, since the diameter is twice the radius:
Diameter = 2 × √(A / π)
3. Step-by-Step Guide: How to Calculate the Diameter of a Circle
To find the diameter of a circle, follow these simple steps:
- Step 1: Identify what you know – the radius, circumference, or area.
- Step 2: Choose the appropriate formula based on the available information.
- Step 3: Substitute the known values into the formula and solve for the diameter.
Example: If a circle has a radius of 7 units, calculate its diameter.
Solution:
Using the formula Diameter = 2 × Radius, we get:
Diameter = 2 × 7 = 14 units
Therefore, the diameter of the circle is 14 units.
4. Diameter vs. Radius: Key Differences
While both diameter and radius define properties of a circle, they are different. The diameter is twice the length of the radius. Here’s a comparison:
| Feature | Diameter | Radius |
|---|---|---|
| Definition | The longest chord passing through the center. | Distance from the center to any point on the edge. |
| Length | Twice the length of the radius. | Half the length of the diameter. |
| Location | Extends from one edge of the circle to the other. | Extends from the center to the edge. |
5. Real-World Examples of Diameter
Understanding diameter isn’t just about formulas; it’s about seeing how math applies to the world around us. Here are a couple of examples:
5.1. Bicycle Wheels
Imagine you’re checking out a new bicycle. The diameter of the wheel is a key measurement because it affects how far you travel with each rotation. A larger diameter means you cover more distance per revolution, making your ride faster and more efficient.
5.2. Pizza Sizes
When ordering a pizza, the size is usually given as the diameter. A 16-inch pizza has a diameter of 16 inches, which tells you how much pizza you’re getting. Knowing the diameter helps you compare the sizes and prices to make the best choice for your appetite and budget.
5.3. Sports Equipment
In sports, the diameter is crucial for equipment like basketball hoops or frisbees. The diameter of a basketball hoop is standardized to ensure fair play, while the diameter of a frisbee affects its aerodynamics and flight characteristics.
5.4. Cooking Pans
When you’re selecting a cooking pan, the diameter is one of the first things you’ll notice. It tells you how much food the pan can hold and whether it will fit on your stovetop. A 10-inch frying pan, for example, has a diameter of 10 inches across its cooking surface.
5.5. Architectural Design
Architects use diameter measurements extensively in building designs. For example, when designing a circular window or a dome, knowing the diameter is essential for structural integrity and aesthetic appeal.
5.6. Piping Systems
In plumbing and construction, the diameter of pipes is critical for ensuring proper flow and pressure. Pipes are often referred to by their diameter, such as a 2-inch pipe, which indicates the inner diameter through which fluids flow.
6. Practical Problems Involving Diameter
To solidify your understanding, let’s work through some practical problems.
6.1. Problem 1: Finding Diameter from Radius
Problem: A circular garden has a radius of 9 meters. What is the diameter of the garden?
Solution:
Using the formula: Diameter = 2 × Radius
Diameter = 2 × 9 meters = 18 meters
Therefore, the diameter of the circular garden is 18 meters.
6.2. Problem 2: Finding Radius from Diameter
Problem: The diameter of a round table is 6 feet. What is the radius of the table?
Solution:
Using the formula: Radius = Diameter / 2
Radius = 6 feet / 2 = 3 feet
Therefore, the radius of the round table is 3 feet.
6.3. Problem 3: Finding Diameter from Circumference
Problem: The circumference of a circular pond is 62.8 feet. What is the diameter of the pond? (Use π = 3.14)
Solution:
Using the formula: Diameter = Circumference / π
Diameter = 62.8 feet / 3.14 = 20 feet
Therefore, the diameter of the circular pond is 20 feet.
6.4. Problem 4: Finding Diameter from Area
Problem: The area of a circular rug is 154 square feet. What is the diameter of the rug? (Use π = 22/7)
Solution:
First, find the radius using the area formula: A = πr²
154 = (22/7) × r²
r² = (154 × 7) / 22 = 49
r = √49 = 7 feet
Now, find the diameter using the radius:
Diameter = 2 × Radius
Diameter = 2 × 7 feet = 14 feet
Therefore, the diameter of the circular rug is 14 feet.
7. Advanced Concepts Related to Diameter
Beyond basic calculations, the diameter plays a role in more complex mathematical concepts.
7.1. Inscribed Angles
An inscribed angle is an angle formed by two chords in a circle that have a common endpoint. If this angle intercepts the diameter, it is always a right angle (90 degrees). This property is useful in various geometric proofs and constructions.
7.2. Thales’ Theorem
Thales’ theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, then the angle ∠ABC is a right angle. This theorem is a special case of the inscribed angle theorem and provides a fundamental understanding of angles in circles.
7.3. Cyclic Quadrilaterals
A cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. According to Ptolemy’s theorem, in a cyclic quadrilateral, the product of the diagonals is equal to the sum of the products of the pairs of opposite sides. Understanding the diameter helps in proving and applying such theorems.
7.4. Calculating the Area of a Semicircle
A semicircle is half of a circle, and its area can be calculated using the diameter. The area of a full circle is A = πr², so the area of a semicircle is half of that. Since r = d/2, the area of a semicircle can be expressed as:
Area of semicircle = (π/8) × d²
This concept is useful in various engineering and architectural applications.
8. Tips and Tricks for Working with Diameters
- Always Double-Check: Ensure you’re using the correct units and formulas when calculating the diameter.
- Use Approximations Wisely: When using π, remember that 3.14 is a common approximation, but for more precise calculations, use the π button on your calculator.
- Visualize: Drawing a diagram can help you understand the problem and prevent errors.
9. Common Mistakes to Avoid
- Confusing Radius and Diameter: Always remember that the diameter is twice the radius.
- Incorrectly Applying Formulas: Ensure you are using the correct formula based on the information given (radius, circumference, or area).
- Forgetting Units: Always include the units in your final answer (e.g., cm, m, inches).
10. Frequently Asked Questions (FAQs) About Diameter
10.1. What is the Diameter of a Circle?
The diameter of a circle is a straight line that passes through the center, connecting two points on the circle’s circumference. It is the longest chord of the circle and divides it into two equal halves.
10.2. How is the Diameter Related to the Radius?
The diameter is twice the length of the radius. Mathematically, this is expressed as Diameter = 2 × Radius.
10.3. Can a Circle Have More Than One Diameter?
Yes, a circle can have infinitely many diameters. Each diameter passes through the center and has endpoints on the circumference, and all diameters of the same circle are equal in length.
10.4. What Happens if the Line Doesn’t Pass Through the Center?
If a line connects two points on the circle’s circumference but doesn’t pass through the center, it’s called a chord, not a diameter.
10.5. Why is the Diameter Important in Real Life?
The diameter is crucial in many real-life applications, such as engineering, construction, and design. It helps in calculating various properties of circular objects, like circumference and area, and ensures accurate measurements and designs.
10.6. What is the Difference Between Diameter and Chord?
A chord is any line segment connecting two points on a circle’s circumference. The diameter is a special type of chord that passes through the center of the circle. Therefore, the diameter is the longest possible chord in a circle.
10.7. What is the Value of Pi (π) and How Is It Used?
Pi (π) is a mathematical constant approximately equal to 3.14159. It represents the ratio of a circle’s circumference to its diameter. Pi is used in formulas to calculate the circumference, area, and volume of circular and spherical shapes.
10.8. How Can You Measure the Diameter of a Physical Circle?
To measure the diameter of a physical circle, you can use a ruler or measuring tape. Place the ruler across the circle, ensuring it passes through the center, and measure the distance from one edge to the opposite edge. This distance is the diameter.
10.9. What Are Some Common Units Used to Measure Diameter?
Common units for measuring diameter include millimeters (mm), centimeters (cm), meters (m), inches (in), and feet (ft). The choice of unit depends on the size of the circle being measured.
10.10. How Do You Find the Area of a Circle If You Know the Diameter?
If you know the diameter of a circle, you can find its area using the following steps:
- Divide the diameter by 2 to find the radius (r = d/2).
- Use the formula for the area of a circle: Area = πr².
- Substitute the value of the radius into the formula and calculate the area.
11. Further Exploration and Resources
- Online Calculators: Use online diameter calculators to quickly solve problems.
- Geometry Textbooks: Consult geometry textbooks for detailed explanations and examples.
- Educational Websites: Explore websites like Khan Academy for video tutorials and practice exercises.
12. Conclusion: Mastering the Diameter of a Circle
Understanding the diameter of a circle is essential for numerous applications in mathematics, science, and everyday life. By grasping the definitions, formulas, and practical uses discussed here, you can confidently tackle problems involving circles.
Do you have more questions or need further clarification? Don’t hesitate to ask on WHAT.EDU.VN, where our community of experts is ready to provide free, accurate answers. Whether you’re a student, professional, or just a curious mind, we’re here to help you explore the world of knowledge with ease. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or reach out via Whatsapp at +1 (206) 555-7890. Visit our website, what.edu.vn, for more information and to ask your questions today!
