What Is the Discriminant? Definition, Formula, and Uses

The discriminant is a powerful concept in algebra that helps us understand the nature of polynomial equations. At WHAT.EDU.VN, we offer a simple, free platform where all your questions can be answered instantly. Delve into the discriminant, its formula, and its significance in determining the nature of roots, including real roots and complex roots, making complex algebra accessible to everyone.

Table of Contents

1. Understanding the Discriminant in Math
2. The Discriminant Formula: Quadratic and Cubic Equations
3. Step-by-Step Guide: How to Find the Discriminant
   • Calculating the Discriminant of a Quadratic Equation
   • Calculating the Discriminant of a Cubic Equation
4. Discriminant and the Nature of Roots: Real, Complex, and Equal
   • When the Discriminant is Positive (D > 0)
   • When the Discriminant is Negative (D < 0)
   • When the Discriminant is Zero (D = 0)
5. Practical Examples: Discriminant in Action
6. Additional Insights: Important Notes on the Discriminant
7. Solved Examples: Mastering Discriminant Calculations
8. Interactive Practice: Test Your Knowledge of the Discriminant
9. FAQ: Discriminant Demystified
10. **Ask Your Question Freely on WHAT.EDU.VN
11. **Conclusion: Unleashing the Power of the Discriminant

1. Understanding the Discriminant in Math

In mathematics, the discriminant of a polynomial is a function of its coefficients that reveals a great deal about the nature of the polynomial’s solutions or roots. It acts as an indicator, distinguishing the types of solutions you’ll encounter without needing to solve the equation directly. Think of it as a detective, providing clues about the roots. Whether they are real numbers, complex numbers, or repeated values, the discriminant offers essential insights.

What does this mean for you?

It means that instead of going through the potentially lengthy process of solving a polynomial equation, you can use the discriminant to quickly determine what kind of solutions to expect. This is especially useful in advanced algebra and calculus where understanding the nature of solutions is crucial.

The discriminant is usually denoted by the Greek letter delta (Δ) or simply by D. The value of the discriminant is a real number, which can be positive, negative, or zero, each indicating a different scenario for the roots of the equation.

2. The Discriminant Formula: Quadratic and Cubic Equations

The discriminant is most commonly used with quadratic and cubic equations, and each type of equation has its own formula. Here’s a breakdown:

Quadratic Equations:

For a quadratic equation in the standard form of ax² + bx + c = 0, the discriminant (D) is given by the formula:

D = b² – 4ac

Where:

• a, b, and c are the coefficients of the quadratic equation.

Cubic Equations:

For a cubic equation in the standard form of ax³ + bx² + cx + d = 0, the discriminant (D) is given by the formula:

D = b²c² – 4ac³ – 4b³d – 27a²d² + 18abcd

Where:

• a, b, c, and d are the coefficients of the cubic equation.

Understanding these formulas is the first step in using the discriminant to analyze polynomial equations. You can use these formulas to calculate the discriminant and then interpret its value to understand the nature of the roots. This approach will save time and provide deeper insights into the behavior of polynomial equations.

3. Step-by-Step Guide: How to Find the Discriminant

Finding the discriminant involves a straightforward process. Here’s how to do it for quadratic and cubic equations:

Calculating the Discriminant of a Quadratic Equation

1. Identify the Coefficients: Start with the quadratic equation in the standard form ax² + bx + c = 0. Identify the values of a, b, and c. These are the numerical coefficients of the respective terms.

2. Apply the Discriminant Formula: The discriminant formula for a quadratic equation is D = b² – 4ac. Substitute the values of a, b, and c into this formula.

3. Calculate the Discriminant: Perform the arithmetic operations to find the value of D. This will involve squaring b, multiplying 4, a, and c, and then subtracting the latter from the former.

4. Interpret the Result:

   • If D > 0, the equation has two distinct real roots.
   • If D < 0, the equation has two distinct complex roots.
   • If D = 0, the equation has one real root (a repeated root).

Example:

Find the discriminant of the quadratic equation 3x² – 5x + 2 = 0.

• a = 3, b = -5, c = 2
• D = (-5)² – 4(3)(2) = 25 – 24 = 1
• Since D = 1 > 0, the equation has two distinct real roots.

Calculating the Discriminant of a Cubic Equation

1. Identify the Coefficients: Start with the cubic equation in the standard form ax³ + bx² + cx + d = 0. Identify the values of a, b, c, and d.

2. Apply the Discriminant Formula: The discriminant formula for a cubic equation is D = b²c² – 4ac³ – 4b³d – 27a²d² + 18abcd. Substitute the values of a, b, c, and d into this formula.

3. Calculate the Discriminant: Perform the arithmetic operations to find the value of D. This calculation is more complex than that for quadratic equations, so be careful with each step.

4. Interpret the Result:

   • If D > 0, the equation has three distinct real roots.
   • If D < 0, the equation has one real root and two complex conjugate roots.
   • If D = 0, the equation has multiple roots, and at least two roots are equal.

Example:

Find the discriminant of the cubic equation x³ – 6x² + 11x – 6 = 0.

• a = 1, b = -6, c = 11, d = -6
• D = (-6)²(11)² – 4(1)(11)³ – 4(-6)³(-6) – 27(1)²(-6)² + 18(1)(-6)(11)(-6)
• D = 4356 – 5324 – 5184 – 972 + 7128 = 0
• Since D = 0, the equation has multiple roots, and at least two roots are equal.

Following these steps will help you accurately find and interpret the discriminant for both quadratic and cubic equations, providing valuable insights into the nature of their roots.

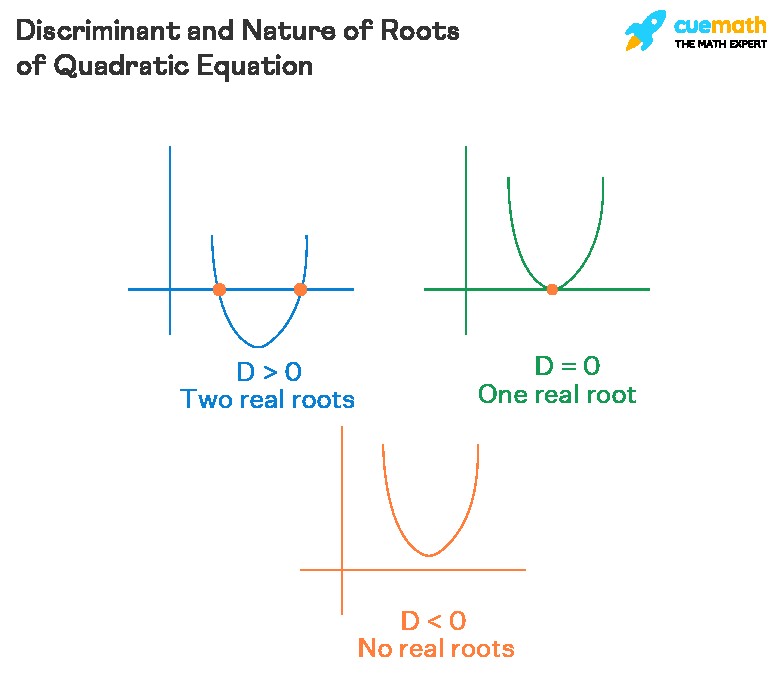
4. Discriminant and the Nature of Roots: Real, Complex, and Equal

The discriminant is a powerful tool for determining the nature of the roots of a quadratic equation without solving the equation itself. Here’s how the value of the discriminant relates to the nature of the roots:

When the Discriminant is Positive (D > 0)

If the discriminant D is greater than zero, the quadratic equation has two distinct real roots. This means that there are two different values of x that will satisfy the equation, and both of these values are real numbers.

Graphically, this corresponds to the parabola intersecting the x-axis at two different points.

When the Discriminant is Negative (D < 0)

If the discriminant D is less than zero, the quadratic equation has two distinct complex roots. This means that there are no real values of x that will satisfy the equation; instead, the solutions involve imaginary numbers. These complex roots always come in conjugate pairs.

Graphically, this corresponds to the parabola not intersecting the x-axis at any point.

When the Discriminant is Zero (D = 0)

If the discriminant D is equal to zero, the quadratic equation has one real root (a repeated root). This means that there is only one value of x that will satisfy the equation, and this value is a real number. In this case, the quadratic equation can be factored into a perfect square.

Graphically, this corresponds to the parabola touching the x-axis at exactly one point.

Summary Table:

Discriminant (D)	Nature of Roots
D > 0	Two distinct real roots
D < 0	Two distinct complex roots
D = 0	One real root (repeated root)

5. Practical Examples: Discriminant in Action

Let’s look at some practical examples of how the discriminant is used:

Example 1: Determining the Nature of Roots

Consider the quadratic equation x² + 4x + 5 = 0. Find the discriminant and determine the nature of the roots.

• a = 1, b = 4, c = 5
• D = b² – 4ac = 4² – 4(1)(5) = 16 – 20 = -4
• Since D < 0, the equation has two distinct complex roots.

Example 2: Finding a Condition for Real Roots

For what values of k does the equation x² + kx + 9 = 0 have real roots?

For the equation to have real roots, the discriminant must be greater than or equal to zero (D ≥ 0).

• D = k² – 4(1)(9) = k² – 36
• For D ≥ 0, k² – 36 ≥ 0
• This inequality holds when k ≤ -6 or k ≥ 6.

Therefore, the equation has real roots when k is less than or equal to -6 or greater than or equal to 6.

Example 3: Verifying a Repeated Root

Show that the equation 4x² – 12x + 9 = 0 has a repeated root.

• a = 4, b = -12, c = 9
• D = b² – 4ac = (-12)² – 4(4)(9) = 144 – 144 = 0
• Since D = 0, the equation has one real root (a repeated root).

These examples illustrate how the discriminant can be used to quickly gain insights into the nature of the roots of a quadratic equation, without needing to solve the equation.

6. Additional Insights: Important Notes on the Discriminant

Here are some key points to remember about the discriminant:

1. The discriminant is derived from the quadratic formula: The quadratic formula is given by x = (-b ± √(b² – 4ac)) / (2a). The term inside the square root, b² – 4ac, is the discriminant.
2. The discriminant only applies to polynomial equations: While the concept of a discriminant can be extended to higher-degree polynomials, it is most commonly used and easily understood in the context of quadratic equations.
3. The discriminant can help in curve sketching: Knowing the nature of the roots (real, complex, repeated) helps in sketching the graph of the quadratic function. For instance, if the discriminant is negative, the parabola does not intersect the x-axis.
4. The discriminant can be used to find conditions for specific types of roots: As shown in the examples, the discriminant can be used to find the values of parameters that make the roots real, complex, or repeated.

7. Solved Examples: Mastering Discriminant Calculations

Let’s go through some more solved examples to reinforce your understanding of discriminant calculations:

Example 4: Finding the Discriminant

Find the discriminant of the quadratic equation 2x² + 7x – 3 = 0.

• a = 2, b = 7, c = -3
• D = b² – 4ac = (7)² – 4(2)(-3) = 49 + 24 = 73
• Therefore, the discriminant is 73.

Example 5: Nature of Roots

Determine the nature of the roots of the quadratic equation x² – 6x + 9 = 0.

• a = 1, b = -6, c = 9
• D = b² – 4ac = (-6)² – 4(1)(9) = 36 – 36 = 0
• Since D = 0, the equation has one real root (a repeated root).

Example 6: Complex Roots

Determine the nature of the roots of the quadratic equation 3x² + 2x + 1 = 0.

• a = 3, b = 2, c = 1
• D = b² – 4ac = (2)² – 4(3)(1) = 4 – 12 = -8
• Since D < 0, the equation has two distinct complex roots.

Example 7: Real and Distinct Roots

Determine the nature of the roots of the quadratic equation x² – 5x + 6 = 0.

• a = 1, b = -5, c = 6
• D = b² – 4ac = (-5)² – 4(1)(6) = 25 – 24 = 1
• Since D > 0, the equation has two distinct real roots.

8. Interactive Practice: Test Your Knowledge of the Discriminant

Test your understanding with these practice questions:

1. Find the discriminant of the equation x² – 8x + 16 = 0.
2. Determine the nature of the roots for the equation 2x² + 5x – 7 = 0.
3. For what value(s) of m does the equation x² + mx + 4 = 0 have one real root?

Check your answers at the end of this article

9. FAQ: Discriminant Demystified

Q: What Is The Discriminant?

A: The discriminant is a part of the quadratic formula (b² – 4ac) that helps determine the nature of the roots of a quadratic equation.

Q: What does a positive discriminant tell us?

A: A positive discriminant indicates that the quadratic equation has two distinct real roots.

Q: What does a negative discriminant tell us?

A: A negative discriminant indicates that the quadratic equation has two distinct complex roots.

Q: What does a zero discriminant tell us?

A: A zero discriminant indicates that the quadratic equation has one real root (a repeated root).

Q: How do I calculate the discriminant?

A: For a quadratic equation in the form ax² + bx + c = 0, the discriminant is calculated using the formula D = b² – 4ac.

Q: Can the discriminant be used for cubic equations?

A: Yes, but the formula is more complex: D = b²c² – 4ac³ – 4b³d – 27a²d² + 18abcd for ax³ + bx² + cx + d = 0.

Q: Why is the discriminant important?

A: The discriminant provides valuable information about the nature of the roots of a quadratic equation without the need to solve the equation.

10. Ask Your Question Freely on WHAT.EDU.VN

Still confused about the discriminant? Need more examples or clarification? Don’t worry! At WHAT.EDU.VN, you can ask any question you have, and our community of experts will provide you with clear, helpful answers. Whether it’s about quadratic equations, cubic equations, or any other math topic, we’re here to help you succeed.

Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN

11. Conclusion: Unleashing the Power of the Discriminant

The discriminant is a powerful tool in algebra that allows you to quickly determine the nature of the roots of a quadratic equation without solving the equation itself. By understanding how to calculate and interpret the discriminant, you can gain valuable insights into the behavior of quadratic equations and tackle more complex math problems with confidence. At what.edu.vn, we’re committed to providing you with the resources and support you need to master these concepts.

Answers to Practice Questions:

1. D = 0
2. Two distinct real roots
3. m = ±4