What Is the Domain of the Function? A Comprehensive Guide

Are you grappling with the concept of the domain of a function? Do you find yourself searching for clear, concise explanations and practical examples? Look no further! WHAT.EDU.VN is here to illuminate this fundamental mathematical idea, providing you with the knowledge and tools to master it. Discover the input values, explore real-world applications, and understand why the domain is crucial for function analysis.

1. Understanding Functions: The Foundation

Before we dive into the specifics of the domain, let’s solidify our understanding of functions themselves. Functions are a cornerstone of mathematics, serving as essential tools for modeling and solving problems across various disciplines. A function is, at its core, a rule that assigns a unique output to each input. Exploring function analysis, mastering domain identification, and understanding range determination are key.

1.1. Relations: The Broader Context

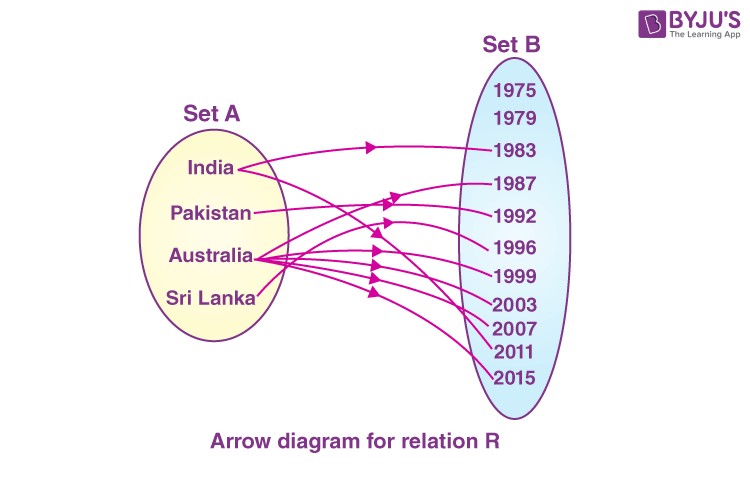
To truly appreciate the nature of a function, it’s helpful to consider the concept of relations. A relation is simply a connection between two sets of information. More formally, a relation is a subset of a Cartesian product. The Cartesian product of two sets, A and B, denoted as A × B, is the set of all possible ordered pairs (a, b), where ‘a’ is an element of A and ‘b’ is an element of B.

1.2. From Relations to Functions: The Key Distinction

While all functions are relations, not all relations are functions. The defining characteristic that distinguishes a function from a more general relation is the “one-to-one” or “many-to-one” requirement. In other words, for a relation to be considered a function, each element in the input set (often called the domain) must be associated with exactly one element in the output set (often called the range).

Example:

Let’s say Set A represents a group of students, and Set B represents their ages.

• Relation (Not a Function): A relation could associate a student with multiple ages, which doesn’t make sense in the real world.
• Function: A function would associate each student with only one age. This is a valid function because each student has a unique age.

1.3. Function Notation: A Concise Language

We typically represent functions using a specific notation:

f(x) = y

• f is the name of the function.
• x represents the input value (an element from the domain).
• y represents the output value (an element from the range) that the function f assigns to the input x.

2. What Is the Domain of the Function? A Deep Dive

The domain of a function is the set of all possible input values (x-values) for which the function is defined and produces a valid output. Domain restrictions, domain analysis, and domain identification are key concepts here. Think of it as the set of all “legal” or “allowed” inputs that you can feed into the function without causing any mathematical errors or undefined results.

2.1. Identifying Domain Restrictions: Common Pitfalls

In many cases, the domain of a function is simply all real numbers. However, certain types of functions have inherent restrictions that limit the possible input values. Here are some of the most common restrictions to watch out for:

• Division by Zero: A fraction with a variable in the denominator is undefined when the denominator equals zero.
• Square Roots of Negative Numbers: In the realm of real numbers, you cannot take the square root (or any even root) of a negative number.
• Logarithms of Non-Positive Numbers: Logarithms are only defined for positive numbers. You cannot take the logarithm of zero or a negative number.
• Tangent Function: The tangent function (tan(x)) is undefined at certain angles (specifically, at odd multiples of π/2).
• Real-World Constraints: In applied problems, the domain may be restricted by physical limitations or logical constraints. For example, if a function models the height of an object, the domain might be restricted to non-negative values of time.

2.2. Finding the Domain: A Step-by-Step Approach

Here’s a systematic approach to determining the domain of a function:

1. Identify Potential Restrictions: Carefully examine the function for any of the common restrictions listed above (division by zero, square roots of negative numbers, logarithms of non-positive numbers, tangent functions, or real-world constraints).
2. Solve for the Restrictions: For each restriction identified, set up an inequality or equation that represents the condition that must be avoided. Solve this inequality or equation to find the values of x that would violate the restriction.
3. Express the Domain: Write the domain as a set of all real numbers except the values that violate the restrictions. This can be expressed using interval notation, set notation, or a combination of both.

2.3. Examples of Domain Determination

Let’s illustrate the process of finding the domain with a few examples:

Example 1: Function with a Denominator

Find the domain of the function:

f(x) = 1 / (x - 3)

• Restriction: Division by zero.
• Solve: x – 3 ≠ 0 => x ≠ 3
• Domain: All real numbers except 3. In interval notation: (-∞, 3) U (3, ∞)

Example 2: Function with a Square Root

Find the domain of the function:

g(x) = √(x + 2)

• Restriction: Square root of a negative number.
• Solve: x + 2 ≥ 0 => x ≥ -2
• Domain: All real numbers greater than or equal to -2. In interval notation: [-2, ∞)

Example 3: Function with a Logarithm

Find the domain of the function:

h(x) = ln(5 - x)

• Restriction: Logarithm of a non-positive number.
• Solve: 5 – x > 0 => x < 5
• Domain: All real numbers less than 5. In interval notation: (-∞, 5)

2.4. Domain and Graphing

The domain of a function has a direct visual representation on its graph. The domain corresponds to the set of all x-values for which the graph exists. If there are any restrictions on the domain, they will be evident on the graph as gaps, holes, or vertical asymptotes.

3. Range and Codomain: The Output Side of the Function

While the domain focuses on the inputs of a function, the range and codomain deal with the outputs.

3.1. Range: The Actual Outputs

The range of a function is the set of all actual output values (y-values) that the function produces when you plug in all possible input values from the domain. To determine function behavior, evaluate output values, and ensure function validity, explore range determination. In simpler terms, it’s the set of all the “results” you get from the function.

3.2. Codomain: The Potential Outputs

The codomain of a function is the set of all possible output values. It’s a broader set that includes the range, but may also include values that the function never actually produces.

Analogy:

Imagine a vending machine.

• Domain: The buttons you can press to select an item.
• Range: The items that the vending machine actually contains and can dispense.
• Codomain: All the possible items that could be in the vending machine, even if they aren’t currently stocked.

3.3. Finding the Range: A More Challenging Task

Determining the range of a function can be more challenging than finding the domain. There’s no single, universal method that works for all functions. However, here are some common techniques:

• Graphing: The easiest way to visualize the range is to graph the function. The range corresponds to the set of all y-values covered by the graph.
• Analyzing the Function: For simpler functions, you may be able to deduce the range by analyzing the function’s behavior. For example, if the function is a square (e.g., f(x) = x^2), you know that the output will always be non-negative, so the range will be [0, ∞).
• Using the Inverse Function: If the function has an inverse, you can find the range of the original function by finding the domain of its inverse.

3.4. Range Examples

Example 1:

Find the range of the function:

f(x) = x^2

• Analysis: Since any real number squared is non-negative, the range is [0, ∞).

Example 2:

Find the range of the function:

g(x) = sin(x)

• Knowledge: The sine function oscillates between -1 and 1, so the range is [-1, 1].

4. Why Is the Domain Important?

Understanding the domain of a function is crucial for several reasons:

• Ensuring Valid Results: Knowing the domain allows you to avoid plugging in invalid inputs that would lead to undefined or nonsensical results.
• Interpreting Function Behavior: The domain provides valuable information about how the function behaves and its limitations.
• Graphing Functions Accurately: The domain is essential for creating accurate graphs of functions.
• Solving Real-World Problems: In applied problems, the domain often represents physical constraints or limitations on the variables involved.
• Defining Inverse Functions: The domain and range are essential for defining inverse functions.

5. Solved Examples: Putting Knowledge into Practice

Let’s solidify your understanding with some solved examples:

Example 1:

Find the domain and range of the function:

f(x) = √(9 - x^2)

• Domain:
  • Restriction: Square root of a negative number.
  • Solve: 9 – x^2 ≥ 0 => x^2 ≤ 9 => -3 ≤ x ≤ 3
  • Domain: [-3, 3]
• Range:
  • The square root function always produces non-negative values. The maximum value of √(9 – x^2) occurs when x = 0, which gives √(9 – 0^2) = 3.
  • Range: [0, 3]

Example 2:

Find the domain and range of the function:

g(x) = (x + 1) / (x - 2)

• Domain:
  • Restriction: Division by zero.
  • Solve: x – 2 ≠ 0 => x ≠ 2
  • Domain: All real numbers except 2. In interval notation: (-∞, 2) U (2, ∞)
• Range: To find the range, let’s solve for x in terms of y:
  • y = (x + 1) / (x – 2)
  • y(x – 2) = x + 1
  • xy – 2y = x + 1
  • xy – x = 2y + 1
  • x(y – 1) = 2y + 1
  • x = (2y + 1) / (y – 1)
  • Restriction: Division by zero.
  • Solve: y – 1 ≠ 0 => y ≠ 1
  • Range: All real numbers except 1. In interval notation: (-∞, 1) U (1, ∞)

6. Frequently Asked Questions (FAQs)

Q1: What’s the difference between the domain and range?

• The domain is the set of all possible input values (x-values) for which a function is defined. The range is the set of all actual output values (y-values) that the function produces.

Q2: How do I find the domain of a function with a square root?

• To find the domain of a function with a square root, set the expression inside the square root greater than or equal to zero and solve for x.

Q3: Can the domain be empty?

• Yes, the domain can be empty. This means there are no possible input values for which the function is defined.

Q4: What is the domain of a polynomial function?

• The domain of a polynomial function is always all real numbers.

Q5: How does the domain affect the graph of a function?

• The domain determines the set of x-values for which the graph exists. Restrictions on the domain will be visible on the graph as gaps, holes, or vertical asymptotes.

7. Need Help with Your Math Questions?

Do you have more questions about the domain of a function, or any other math topic? Don’t struggle alone! At WHAT.EDU.VN, we provide a free platform where you can ask any question and receive prompt, accurate answers from knowledgeable experts.

7.1. Why Choose WHAT.EDU.VN?

• Free: Our service is completely free to use. Ask as many questions as you like without any cost.
• Fast: Get answers to your questions quickly. Our experts are available to provide timely assistance.
• Accurate: Receive reliable and accurate answers from qualified individuals.
• Comprehensive: We cover a wide range of subjects, so you can get help with any topic you’re struggling with.
• Easy to Use: Our platform is designed to be user-friendly and intuitive, making it easy to ask questions and find answers.

7.2. How to Ask a Question on WHAT.EDU.VN

1. Visit our website: WHAT.EDU.VN
2. Create a free account (if you don’t already have one).
3. Navigate to the “Ask a Question” section.
4. Type your question clearly and concisely.
5. Select the appropriate subject category.
6. Submit your question.

Our experts will review your question and provide a detailed answer as soon as possible.

8. Real-World Applications of Domain and Range

The concepts of domain and range aren’t just abstract mathematical ideas; they have practical applications in various fields:

• Physics: In physics, the domain might represent the possible values of time or distance, while the range could represent the corresponding values of velocity or acceleration.
• Engineering: Engineers use domain and range to analyze the behavior of systems and ensure that they operate within safe and reliable limits.
• Economics: Economists use functions to model economic phenomena, and the domain and range represent the possible values of variables such as price, quantity, and income.
• Computer Science: In computer science, the domain and range are important for defining the inputs and outputs of algorithms and functions.

9. Advanced Topics Related to Domain and Range

Once you have a solid understanding of the basic concepts of domain and range, you can explore more advanced topics:

• Inverse Functions: The domain and range of a function are closely related to the domain and range of its inverse function.
• Composite Functions: The domain of a composite function depends on the domains of the individual functions that make it up.
• Multivariable Functions: The concept of domain and range can be extended to functions of multiple variables.

10. Practice Problems

Test your understanding with these practice problems:

1. Find the domain and range of the function f(x) = √(x – 4) / (x – 6).
2. Find the domain and range of the function g(x) = e^(-x).
3. Find the domain and range of the function h(x) = tan(x).

11. Call to Action

Don’t let math questions hold you back! Visit WHAT.EDU.VN today and experience the ease and convenience of our free question-and-answer platform. Our team of experts is ready to help you conquer any math challenge.

Address: 888 Question City Plaza, Seattle, WA 98101, United States

WhatsApp: +1 (206) 555-7890

Website: what.edu.vn

Ask your question now and unlock your full potential!