What Is The Midpoint Formula? It’s a foundational concept in geometry that helps you find the exact center point between two given points. At WHAT.EDU.VN, we make understanding math easy and accessible, offering clear explanations and helpful resources. Discover how to use the midpoint formula, its applications, and why it’s an essential tool in various fields. Unlock your mathematical potential with us today.
1. Understanding the Core: What is the Midpoint?
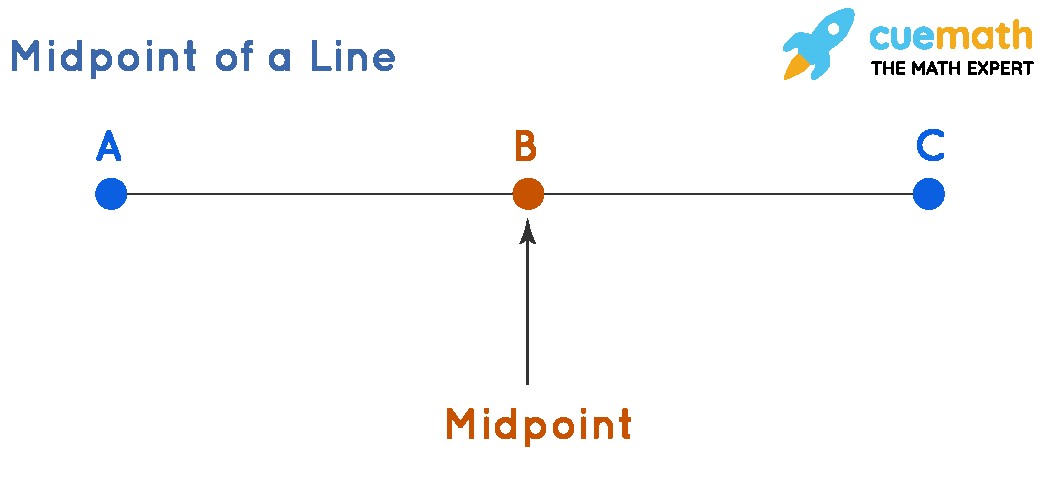
A midpoint is the point that sits precisely in the middle of a line segment. Imagine connecting two points with a straight line; the midpoint is the spot exactly halfway between them. This point divides the line segment into two equal parts. It’s crucial to remember that midpoints exist only for line segments, not for infinite lines or rays. This fundamental concept is essential for various geometric calculations and constructions. Think of it like finding the center of a bridge span – it has to be exactly in the middle to ensure stability.
1.1. Key Characteristics of a Midpoint
- Equidistant: The midpoint is at an equal distance from both endpoints of the line segment.
- Bisector: A line passing through the midpoint bisects the line segment, dividing it into two congruent segments.
- Uniqueness: For any given line segment, there is only one midpoint.
2. The Midpoint Formula: Your Key to Finding the Center
The midpoint formula provides a simple yet powerful way to calculate the coordinates of the midpoint between two points in a coordinate plane. If you have two points, let’s say A (x₁, y₁) and B (x₂, y₂), the midpoint M (x_m, y_m) can be found using the following formulas:
- x_m = (x₁ + x₂) / 2
- y_m = (y₁ + y₂) / 2
In simpler terms, the x-coordinate of the midpoint is the average of the x-coordinates of the two endpoints, and the y-coordinate of the midpoint is the average of the y-coordinates of the two endpoints.
2.1. Breaking Down the Formula
- Addition: Sum the x-coordinates (x₁ + x₂) and the y-coordinates (y₁ + y₂).
- Division: Divide each sum by 2.
- Coordinates: The results give you the x and y coordinates of the midpoint (x_m, y_m).
2.2. Why is the Midpoint Formula so Useful?
The midpoint formula isn’t just a theoretical concept; it has practical applications in various fields:
- Geometry: Finding the center of shapes and figures.
- Navigation: Determining the halfway point on a journey.
- Computer Graphics: Calculating the center of objects for transformations.
- Construction: Ensuring precise measurements in building projects.
3. Deriving the Midpoint Formula: A Visual Explanation
To truly understand the midpoint formula, let’s explore its derivation. Imagine two points on a number line. The midpoint would be the average of those two numbers. For example, the midpoint between 5 and 9 is (5 + 9) / 2 = 7.
Now, extend this concept to a coordinate plane. The x-coordinate of the midpoint is simply the average of the x-coordinates of the endpoints, and the y-coordinate of the midpoint is the average of the y-coordinates of the endpoints. This is why we sum the x-values and divide by 2, and do the same for the y-values.
3.1. Step-by-Step Derivation
- Consider Two Points: Let A (x₁, y₁) and B (x₂, y₂) be two points on a coordinate plane.
- Horizontal Distance: The horizontal distance between A and B is |x₂ – x₁|.
- Half the Horizontal Distance: To find the x-coordinate of the midpoint, take half of this distance and add it to x₁: x_m = x₁ + (x₂ – x₁) / 2 = (x₁ + x₂) / 2.
- Vertical Distance: Similarly, the vertical distance between A and B is |y₂ – y₁|.
- Half the Vertical Distance: To find the y-coordinate of the midpoint, take half of this distance and add it to y₁: y_m = y₁ + (y₂ – y₁) / 2 = (y₁ + y₂) / 2.
- Midpoint Coordinates: Therefore, the midpoint M has coordinates ((x₁ + x₂) / 2, (y₁ + y₂) / 2).
3.2. Practical Example
Let’s find the midpoint between points X (5, 3) and Y (7, 8).
- x_m = (5 + 7) / 2 = 6
- y_m = (3 + 8) / 2 = 11/2
The midpoint M is (6, 11/2).
4. Methods to Find the Midpoint: Visual and Analytical
Finding the midpoint can be approached in different ways, depending on the situation:
4.1. Visual Method (for Horizontal and Vertical Lines)
If the line segment is either horizontal or vertical, you can find the midpoint by measuring the length of the segment and dividing by 2. Then, count that distance from either endpoint to find the midpoint.
- Horizontal Line: Count the units horizontally from one endpoint to the other, divide by two, and move that many units from either endpoint.
- Vertical Line: Count the units vertically from one endpoint to the other, divide by two, and move that many units from either endpoint.
4.2. Analytical Method (Using the Midpoint Formula)
This method involves using the midpoint formula directly. Identify the coordinates of the endpoints and apply the formula to find the midpoint.
- Step 1: Identify the coordinates of the two endpoints (x₁, y₁) and (x₂, y₂).
- Step 2: Apply the midpoint formula: M = ((x₁ + x₂) / 2, (y₁ + y₂) / 2).
- Step 3: Simplify the expression to find the coordinates of the midpoint.
4.3. Construction Method
You can also find the midpoint using a compass and straightedge. This method is particularly useful in geometry constructions.
- Draw a Line Segment: Start with the line segment for which you want to find the midpoint.
- Create Arcs: Place the compass on one endpoint and draw an arc that extends more than halfway across the segment.
- Repeat: Without changing the compass width, place the compass on the other endpoint and draw another arc. The arcs should intersect.
- Connect Intersections: Use the straightedge to draw a line connecting the two points where the arcs intersect. This line will intersect the original line segment at its midpoint.
4.4. Finding an Endpoint When You Know the Midpoint
Sometimes, you might know the midpoint and one endpoint, and you need to find the other endpoint. Here’s how to do it:
Given:
- Midpoint R (x_r, y_r)
- Endpoint Q (x₂, y₂)
Find: Endpoint P (x₁, y₁)
Formulas:
- x₁ = 2x_r – x₂
- y₁ = 2y_r – y₂
Example: Midpoint R is (4, 6) and endpoint Q is (8, 10).
- x₁ = 2(4) – 8 = 0
- y₁ = 2(6) – 10 = 2
Therefore, the coordinates of point P are (0, 2).
5. Formulas Related to the Midpoint: Expanding Your Geometric Toolkit
The midpoint formula is closely related to other geometric concepts, such as the centroid of a triangle and the section formula. Understanding these connections can enhance your problem-solving abilities.
5.1. Centroid of a Triangle Formula
The centroid of a triangle is the point where the three medians of the triangle intersect. A median is a line segment from a vertex to the midpoint of the opposite side. For a triangle with vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃), the coordinates of the centroid (x_c, y_c) are:
- x_c = (x₁ + x₂ + x₃) / 3
- y_c = (y₁ + y₂ + y₃) / 3
The centroid divides each median in a 2:1 ratio.
5.2. Section Formula
The section formula helps find the coordinates of a point that divides a line segment in a given ratio. If a point divides the line segment joining (x₁, y₁) and (x₂, y₂) in the ratio m:n, the coordinates of the point (x, y) are:
- x = (mx₂ + nx₁) / (m + n)
- y = (my₂ + ny₁) / (m + n)
If the point divides the line segment internally, use the above formulas directly. If it divides the line segment externally, use the following formulas:
- x = (mx₂ – nx₁) / (m – n)
- y = (my₂ – ny₁) / (m – n)
5.3. Key Properties of Midpoints
- Equal Division: The midpoint divides a line segment into two equal parts (1:1 ratio).
- Line Bisector: The bisector of a line segment intersects it at the midpoint.
6. Midpoint Formula Examples: Putting Knowledge into Practice
Let’s walk through some examples to illustrate how to use the midpoint formula effectively.
6.1. Example 1: Finding the Center of a Circle
The diameter of a circle has endpoints (2, -3) and (-6, 5). Find the coordinates of the center of the circle.
- Solution: The center of the circle is the midpoint of the diameter. Let (x₁, y₁) = (2, -3) and (x₂, y₂) = (-6, 5).
- x_m = (2 + (-6)) / 2 = -4 / 2 = -2
- y_m = (-3 + 5) / 2 = 2 / 2 = 1
Therefore, the center of the circle is (-2, 1).
6.2. Example 2: Finding an Unknown Coordinate
Consider the line segment AB with endpoints (1, h) and (5, 7). The midpoint of AB is (3, -2). Find the value of h.
- Solution: Let (x₁, y₁) = (1, h) and (x₂, y₂) = (5, 7). The midpoint is (3, -2).
- Using the midpoint formula for the y-coordinate: (h + 7) / 2 = -2
- Solving for h: h + 7 = -4 => h = -11
Therefore, the value of h is -11.
6.3. Example 3: Another Coordinate Challenge
The endpoints of a line segment are (2, h) and (4, 7). The midpoint is (3, -1). Find the value of h.
- Solution: Let (x₁, y₁) = (2, h) and (x₂, y₂) = (4, 7). The midpoint is (3, -1).
- Using the midpoint formula for the y-coordinate: (h + 7) / 2 = -1
- Solving for h: h + 7 = -2 => h = -9
Therefore, the value of h is -9.
7. Practice Questions on Midpoint Formula
Test your understanding with these practice questions:
- Find the midpoint of the line segment with endpoints (-3, 4) and (5, -2).
- The midpoint of a line segment is (2, 1). One endpoint is (-1, 3). Find the coordinates of the other endpoint.
- A triangle has vertices A(1, 2), B(4, 6), and C(7, 2). Find the coordinates of the midpoint of side BC.
(Answers: 1. (1, 1), 2. (5, -1), 3. (11/2, 4))
8. Frequently Asked Questions (FAQs) on Midpoint Formula
8.1. What is the Midpoint Formula in Coordinate Geometry?
The midpoint formula in coordinate geometry is used to find the exact center point of a line segment. Given two points (x₁, y₁) and (x₂, y₂), the midpoint is ((x₁ + x₂) / 2, (y₁ + y₂) / 2).
8.2. How to Use Midpoint Formula?
- Identify the endpoints of the line segment.
- Note their coordinates (x₁, y₁) and (x₂, y₂).
- Add the x-coordinates and divide by 2: (x₁ + x₂) / 2.
- Add the y-coordinates and divide by 2: (y₁ + y₂) / 2.
- The midpoint is ((x₁ + x₂) / 2, (y₁ + y₂) / 2).
8.3. What is Meant by Midpoint?
The midpoint is the point exactly in the middle of a line segment. It’s equidistant from both endpoints, dividing the segment into two equal parts.
8.4. What is the Midpoint Formula in Words?
The midpoint is found by averaging the x-coordinates and averaging the y-coordinates of the two endpoints.
8.5. Can Midpoint be a Fraction?
Yes, the coordinates of the midpoint can be fractions if the sum of the coordinates of the endpoints is not divisible by 2.
8.6. Why is the Midpoint Formula Important?
The midpoint formula is essential for various applications in geometry, navigation, computer graphics, and construction. It helps find the center of shapes, determine halfway points, and ensure precise measurements.
8.7. How do you Calculate Midpoint?
Use the formula: ((x₁ + x₂) / 2, (y₁ + y₂) / 2), where (x₁, y₁) and (x₂, y₂) are the coordinates of the endpoints.
8.8. Can the Midpoint be Zero?
Yes, if the sum of the x-coordinates and the sum of the y-coordinates are both zero, the midpoint will be (0, 0).
8.9. What is the Midpoint of a Curve?
The midpoint of a curve typically refers to the midpoint of the largest chord that can be drawn within the curve, such as the diameter of a circle.
8.10. What is the Midpoint of a Line?
The midpoint of a line segment is the point equidistant from its endpoints, calculated using the midpoint formula.
8.11. What is the Midpoint of a Circle?
The midpoint of a circle is its center, equidistant from all points on the circumference.
8.12. What is the Midpoint of a Triangle?
While a triangle doesn’t have a single “midpoint,” the centroid is often considered its center. The centroid is the point where the medians of the triangle intersect.
9. Need More Help? Get Your Questions Answered at WHAT.EDU.VN
Finding the midpoint can sometimes feel challenging, especially when dealing with complex problems. But don’t worry, WHAT.EDU.VN is here to help. Our platform is designed to provide you with quick, accurate, and free answers to all your questions.
Are you struggling with a specific math problem? Do you need clarification on a concept? Just ask! Our community of experts and knowledgeable users are ready to assist you.
9.1. How WHAT.EDU.VN Can Help
- Free Question Answering: Ask any question and receive helpful answers from our community.
- Expert Assistance: Connect with experts in various fields for detailed explanations.
- Easy-to-Use Platform: Our website is designed to be intuitive and user-friendly, making it easy to find the information you need.
9.2. Take Action Now!
Don’t let your questions go unanswered. Visit WHAT.EDU.VN today and ask anything. Whether it’s a math problem, a science question, or anything else, we’re here to provide the answers you need.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn
Join our community and experience the convenience of having your questions answered quickly and easily. We’re committed to making learning accessible to everyone. Start asking and exploring today!