What Is The Numerator And Denominator? Understanding fractions can be easy. At WHAT.EDU.VN, we break down the parts of a fraction, making math simple and accessible for everyone. Discover the secrets of numerators and denominators!
1. Understanding Numerator and Denominator
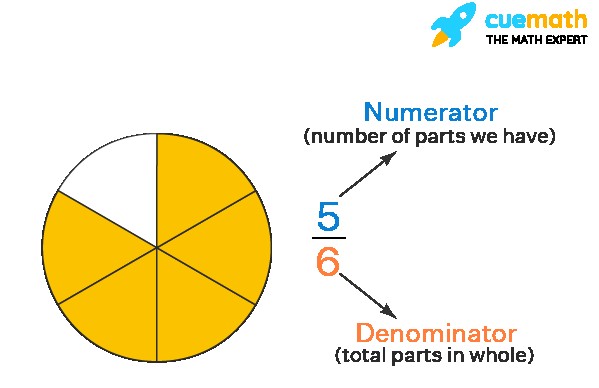
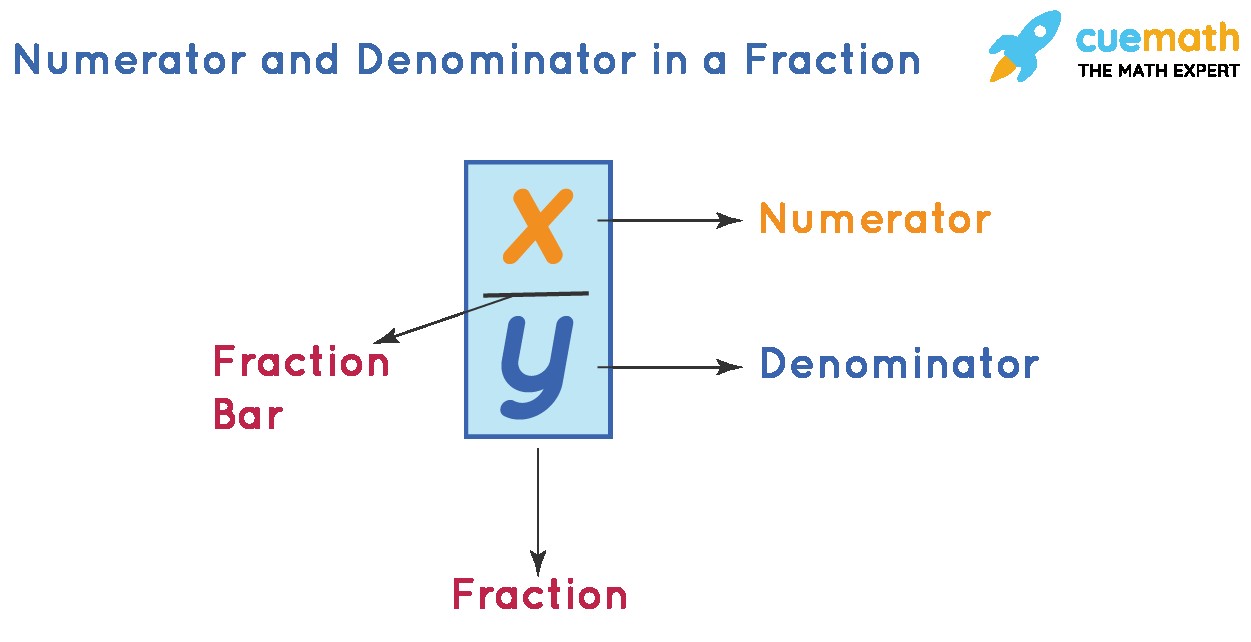
In mathematics, a fraction represents a part of a whole or, more generally, any number of equal parts. A fraction is written with two numbers separated by a line. This line is known as the fraction bar. The number above the fraction bar is the numerator, and the number below the fraction bar is the denominator. Let’s delve into each of these terms.
-
Numerator: The numerator indicates how many parts of the whole are being considered. It represents the selected parts. For instance, if you have a pizza cut into eight slices and you take three, the numerator would be 3, indicating you have three slices.
-
Denominator: The denominator indicates the total number of equal parts that make up the whole. In the pizza example, if the pizza is cut into eight slices, the denominator is 8, representing the total number of slices.
To put it simply:
- Numerator = Selected parts
- Denominator = Total parts
1.1. The Role of the Numerator
The numerator plays a crucial role in defining the value of a fraction.
- Zero Numerator: If the numerator is zero, the entire fraction equals zero. This is because you have zero parts of the whole.
- Numerator Greater Than Denominator: When the numerator is larger than the denominator, the fraction is an improper fraction. This means the fraction’s value is greater than one. For example, 5/4 is an improper fraction, representing more than one whole.
- Numerator Equal to Denominator: If the numerator equals the denominator, the fraction equals one. This signifies that you have all the parts of the whole. For example, 8/8 is equal to one whole.
1.2. The Role of the Denominator
The denominator is equally important as it determines the size of each part that makes up the whole.
- Zero Denominator: A denominator cannot be zero. Division by zero is undefined in mathematics.
- Denominator and Equal Parts: The denominator indicates the number of equal parts. If the denominator is 4, the whole is divided into four equal parts.
- Proper Fractions: When the denominator is greater than the numerator, the fraction is a proper fraction. This means the fraction’s value is less than one. For example, 3/4 is a proper fraction, representing less than one whole.
2. Numerator vs Denominator: Key Differences
Understanding the difference between the numerator and denominator is vital in grasping fractions. Here’s a detailed comparison.
| Feature | Numerator | Denominator |
|---|---|---|
| Position | Above the fraction bar | Below the fraction bar |
| Represents | The number of parts selected | The total number of equal parts |
| Value When Zero | If zero, the entire fraction is zero | Cannot be zero |
| Fraction Type | Determines if the fraction is proper, improper, or equal to one | Determines the size of each part |
| In Division | Acts as the dividend (the number being divided) | Acts as the divisor (the number dividing) |
| Example (in 3/4) | 3 | 4 |

2.1. Understanding Proper and Improper Fractions
Fractions are categorized into proper and improper fractions based on the relationship between the numerator and the denominator.
- Proper Fraction: A proper fraction is one where the numerator is less than the denominator. The value of a proper fraction is always less than 1. Examples include 1/2, 3/4, and 5/8.
- Improper Fraction: An improper fraction is one where the numerator is greater than or equal to the denominator. The value of an improper fraction is always greater than or equal to 1. Examples include 5/3, 7/2, and 4/4.
Improper fractions can also be expressed as mixed numbers, which combine a whole number and a proper fraction. For example, 5/3 can be written as 1 2/3.
2.2. Zero in Numerators and Denominators
The presence of zero in either the numerator or the denominator has significant implications.
- Zero Numerator: As mentioned, if the numerator is zero, the value of the fraction is zero, regardless of the denominator (as long as the denominator is not zero).
- Zero Denominator: A zero denominator makes the fraction undefined. Division by zero is not allowed in mathematics because it leads to illogical results.
3. Real-World Applications of Numerators and Denominators
Fractions, and thus numerators and denominators, are not just abstract mathematical concepts. They are used extensively in everyday life.
3.1. Cooking and Baking
Recipes often use fractions to specify the amount of ingredients needed. For example, a recipe might call for 1/2 cup of flour or 3/4 teaspoon of salt. Here, the numerator indicates the quantity, and the denominator indicates the unit of measurement.
3.2. Measurement
Measurements of length, weight, and volume often involve fractions. For example, you might measure a piece of wood to be 2 1/2 feet long or weigh ingredients to be 1/4 pound.
3.3. Time
Time is frequently expressed in fractions. For instance, 15 minutes is 1/4 of an hour, and 30 minutes is 1/2 of an hour.
3.4. Money
Money also involves fractions, especially when dealing with cents. For example, 50 cents is 1/2 of a dollar, and 25 cents is 1/4 of a dollar.
3.5. Data Representation
In statistics and data analysis, fractions are used to represent proportions and percentages. For example, if 60 out of 100 people prefer coffee, the fraction 60/100 (or 3/5) represents the proportion of people who prefer coffee.
4. Numerators and Denominators in Division
Fractions are closely related to division. In fact, a fraction can be thought of as a division problem. The numerator is the dividend (the number being divided), and the denominator is the divisor (the number doing the dividing).
4.1. Fraction as Division
The fraction x/y is the same as x ÷ y. This means you are dividing x into y equal parts. For example, the fraction 3/4 is the same as 3 ÷ 4, which equals 0.75.
4.2. Simplifying Fractions
Simplifying fractions involves dividing both the numerator and the denominator by their greatest common factor (GCF) to reduce the fraction to its simplest form. For example, the fraction 6/8 can be simplified by dividing both the numerator and denominator by 2, resulting in 3/4.
4.3. Converting Division Problems to Fractions
Any division problem can be written as a fraction. For example, if you want to divide 5 by 8, you can write it as the fraction 5/8. This makes it easier to visualize and understand the division process.
5. Tips and Tricks to Remember Numerators and Denominators
Remembering which number is the numerator and which is the denominator can be tricky. Here are some helpful tips and tricks.
5.1. Mnemonics
- Numerator Up: Remember that the numerator is “up” above the fraction bar.
- Denominator Down: The denominator is “down” below the fraction bar.
5.2. Visualize
Think of a pizza. The denominator is the total number of slices, and the numerator is the number of slices you have.
5.3. Real-World Examples
Relate fractions to real-world situations. For example, if you are sharing a cake with friends, the denominator is the number of people sharing the cake, and the numerator is the number of slices each person gets.
5.4. Practice
The more you work with fractions, the easier it will become to remember which number is the numerator and which is the denominator.
6. Common Mistakes to Avoid
When working with fractions, it’s easy to make mistakes. Here are some common errors to watch out for.
6.1. Confusing Numerator and Denominator
One of the most common mistakes is confusing the numerator and the denominator. Always double-check which number is on top and which is on the bottom.
6.2. Zero Denominator
Forgetting that a denominator cannot be zero is another common mistake. Remember, division by zero is undefined.
6.3. Incorrect Simplification
When simplifying fractions, make sure to divide both the numerator and the denominator by the same number.
6.4. Adding or Subtracting Fractions Incorrectly
When adding or subtracting fractions, you need to have a common denominator. Adding or subtracting numerators without a common denominator will lead to incorrect results.
7. Interactive Exercises to Practice
Practice makes perfect when it comes to understanding numerators and denominators. Here are some interactive exercises to help solidify your knowledge.
7.1 Identify the Numerator and Denominator
For each of the following fractions, identify the numerator and the denominator:
a) 2/3
b) 5/8
c) 1/4
d) 7/9
e) 11/15
7.2 Proper or Improper?
Determine whether each of the following fractions is proper or improper:
a) 3/5
b) 7/2
c) 4/4
d) 1/3
e) 9/4
7.3 Simplify the Fractions
Simplify each of the following fractions to their simplest form:
a) 4/8
b) 6/9
c) 10/15
d) 8/12
e) 12/18
7.4 Real-World Problems
Solve the following real-world problems involving fractions:
a) Sarah ate 2/5 of a pizza. What fraction of the pizza is left?
b) John spent 1/3 of his day at school. How many hours did he spend at school?
c) Emily used 3/4 cup of sugar for a recipe. How much sugar is left if she started with 2 cups?
8. Advanced Concepts Related to Numerators and Denominators
Once you have a solid understanding of the basics, you can explore more advanced concepts related to numerators and denominators.
8.1 Equivalent Fractions
Equivalent fractions are fractions that have the same value but different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions. You can create equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number.
8.2 Comparing Fractions
To compare fractions, you need to have a common denominator. Once the denominators are the same, you can compare the numerators. The fraction with the larger numerator is the larger fraction.
8.3 Operations with Fractions
Performing operations with fractions involves adding, subtracting, multiplying, and dividing fractions. Each operation has its own set of rules and steps.
8.3.1 Adding Fractions
To add fractions, you need a common denominator. Once you have a common denominator, add the numerators and keep the denominator the same. For example:
1/4 + 2/4 = (1+2)/4 = 3/4
8.3.2 Subtracting Fractions
To subtract fractions, you also need a common denominator. Subtract the numerators and keep the denominator the same. For example:
3/5 – 1/5 = (3-1)/5 = 2/5
8.3.3 Multiplying Fractions
To multiply fractions, multiply the numerators together and multiply the denominators together. For example:
2/3 1/2 = (21)/(3*2) = 2/6 = 1/3
8.3.4 Dividing Fractions
To divide fractions, multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example:
1/2 ÷ 3/4 = 1/2 4/3 = (14)/(2*3) = 4/6 = 2/3
9. Understanding Ratios and Proportions
Fractions are closely related to ratios and proportions. A ratio is a comparison of two quantities, and it can be written as a fraction. A proportion is an equation that states that two ratios are equal.
9.1 Ratios
A ratio compares two quantities. For example, if there are 3 apples and 5 oranges, the ratio of apples to oranges is 3:5, which can also be written as the fraction 3/5.
9.2 Proportions
A proportion states that two ratios are equal. For example, if 2/3 = 4/6, then the two ratios are proportional. Proportions are often used to solve problems involving scaling and measurement.
10. Visual Aids for Learning
Visual aids can be incredibly helpful in understanding fractions, numerators, and denominators.
10.1 Fraction Bars
Fraction bars are visual representations of fractions that show how much of a whole each fraction represents. They can be used to compare fractions, add fractions, and subtract fractions.
10.2 Pie Charts
Pie charts are circular charts that are divided into slices to represent different fractions of a whole. They are often used to show how a total quantity is divided among different categories.
10.3 Number Lines
Number lines can be used to represent fractions visually. By dividing the number line into equal parts, you can show where each fraction falls on the line.
11. Strategies for Teaching Numerators and Denominators
Teaching numerators and denominators can be challenging, but there are several strategies that can help students grasp the concepts more easily.
11.1 Hands-On Activities
Using hands-on activities can make learning about fractions more engaging and memorable. For example, you can use manipulatives like fraction tiles, pattern blocks, or even food items like pizza or cookies to demonstrate the concept of fractions.
11.2 Real-World Connections
Connecting fractions to real-world situations can help students see the relevance of what they are learning. Use examples from cooking, measurement, time, and money to illustrate how fractions are used in everyday life.
11.3 Visual Aids
Using visual aids like fraction bars, pie charts, and number lines can help students visualize fractions and understand the relationship between the numerator and the denominator.
11.4 Collaborative Learning
Encouraging students to work together and discuss their understanding of fractions can help them clarify their thinking and learn from each other. Use group activities and discussions to promote collaborative learning.
12. Addressing Common Misconceptions
There are several common misconceptions that students often have about fractions, numerators, and denominators. Addressing these misconceptions directly can help students develop a more accurate understanding of the concepts.
12.1 Misconception: The Denominator Represents the Number of Parts Taken
Correction: The denominator represents the total number of equal parts that make up the whole, not the number of parts taken.
12.2 Misconception: Fractions Must Always Be Less Than 1
Correction: Fractions can be greater than 1 (improper fractions) or equal to 1.
12.3 Misconception: You Can Only Add Fractions With the Same Numerator
Correction: You can only add fractions with the same denominator.
12.4 Misconception: Simplifying a Fraction Changes Its Value
Correction: Simplifying a fraction does not change its value; it only changes the way it is written.
13. Advanced Applications in Higher Mathematics
The concepts of numerators and denominators are fundamental to many areas of higher mathematics.
13.1 Algebra
In algebra, fractions are used extensively in algebraic expressions and equations. Understanding how to manipulate fractions is essential for solving algebraic problems.
13.2 Calculus
In calculus, fractions are used to define rates of change and areas under curves. The concept of a limit, which is fundamental to calculus, involves fractions and their behavior as the denominator approaches zero.
13.3 Number Theory
In number theory, fractions are used to study the properties of numbers and their relationships. Concepts like rational numbers, irrational numbers, and continued fractions all rely on an understanding of numerators and denominators.
14. Fun Facts About Fractions
Fractions are not only useful but also have some interesting and fun facts associated with them.
14.1 The Word “Fraction” Comes From Latin
The word “fraction” comes from the Latin word “fractio,” which means “to break.”
14.2 Egyptians Used Fractions Over 3,500 Years Ago
The ancient Egyptians were among the first to use fractions. Their system of fractions was based on unit fractions, which are fractions with a numerator of 1.
14.3 The Fraction Bar Was Introduced in the 12th Century
The fraction bar, which separates the numerator and the denominator, was introduced by the Arab mathematician Al-Hassar in the 12th century.
14.4 Fractions Are Used in Music
In music, fractions are used to represent the length of notes. For example, a quarter note is 1/4 of a whole note.
15. Numerator and Denominator FAQs
Let’s tackle some frequently asked questions about numerators and denominators.
15.1 What is the significance of the numerator and denominator in a fraction?
The numerator indicates how many parts of the whole are being considered, while the denominator indicates the total number of equal parts that make up the whole.
15.2 How can I easily remember which number is the numerator and which is the denominator?
Use the mnemonic “Numerator Up” and “Denominator Down” to remember their positions in the fraction.
15.3 What happens if the denominator of a fraction is zero?
If the denominator is zero, the fraction is undefined because division by zero is not allowed.
15.4 How do you add or subtract fractions with different denominators?
To add or subtract fractions with different denominators, you need to find a common denominator first.
15.5 Are fractions only used in math class?
No, fractions are used in many real-world situations, such as cooking, measurement, time, and money.
15.6 What is the difference between a proper and an improper fraction?
In a proper fraction, the numerator is less than the denominator. In an improper fraction, the numerator is greater than or equal to the denominator.
15.7 Can an improper fraction be written as a mixed number?
Yes, an improper fraction can be converted to a mixed number, which consists of a whole number and a proper fraction.
16. Need More Help? Ask WHAT.EDU.VN!
Are you still struggling with numerators and denominators? Do you have more questions about fractions or other math topics? Don’t worry! At WHAT.EDU.VN, we provide free, fast, and accurate answers to all your questions. Whether you’re a student, a teacher, or just someone curious about the world, we’re here to help.
16.1 How to Ask a Question on WHAT.EDU.VN
Asking a question on WHAT.EDU.VN is easy. Just visit our website and submit your question in the designated form. Our team of experts will review your question and provide a detailed, easy-to-understand answer.
16.2 Benefits of Using WHAT.EDU.VN
- Free: Our services are completely free. You can ask as many questions as you like without any cost.
- Fast: We strive to provide answers as quickly as possible. You won’t have to wait long to get the help you need.
- Accurate: Our team of experts ensures that all answers are accurate and reliable.
- Easy to Understand: We provide answers in a clear and simple language that everyone can understand.
- Comprehensive: We cover a wide range of topics, from math and science to history and literature.
17. Ready to Take the Next Step?
Now that you have a solid understanding of numerators and denominators, you’re ready to tackle more advanced math concepts. Keep practicing, keep asking questions, and never stop learning!
Fractions are a fundamental part of mathematics and are used in many areas of life. By understanding the numerator and the denominator, you can unlock the power of fractions and use them to solve problems, make calculations, and understand the world around you.
So, the next time you encounter a fraction, remember what you’ve learned here and confidently tackle the problem. And if you ever get stuck, don’t hesitate to reach out to us at WHAT.EDU.VN. We’re always here to help you on your learning journey.
18. Don’t Hesitate! Ask Your Question Now!
Do you have a burning question about fractions, numerators, denominators, or any other topic? Don’t hesitate! Visit WHAT.EDU.VN today and get your question answered for free. Our team of experts is ready to help you understand even the most complex concepts.
18.1 Connect With Us
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
18.2 Why Wait? Get Your Answers Now!
Why struggle with difficult concepts when help is just a click away? Visit WHAT.EDU.VN now and experience the ease and convenience of our free question-and-answer service. We’re here to support you every step of the way.
This comprehensive guide should give anyone a strong foundation in numerators and denominators, but if you still have questions, what.edu.vn is the place to get them answered!