What is the radius of a circle? It’s a question that pops up in geometry, engineering, and even everyday life. At WHAT.EDU.VN, we break down this fundamental concept, offering clarity and practical applications. Discover the definition, formulas, and methods to find the radius, ensuring a solid understanding. Learn about circle measurements, circumference, and area effortlessly.
1. Understanding the Radius of a Circle
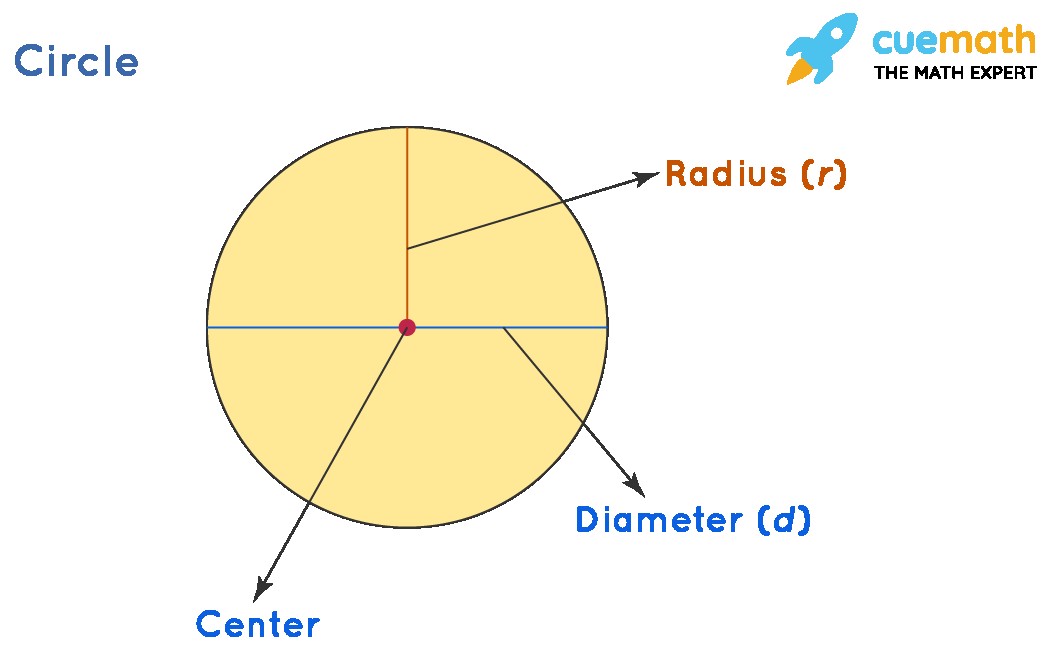
The radius of a circle is more than just a line; it’s a fundamental concept in geometry. It’s the distance from the center of the circle to any point on its edge, also known as the circumference. Think of it as the spoke of a wheel, connecting the hub (center) to the rim (circumference).
1.1. Defining the Radius
The radius is a line segment that begins at the exact center of a circle and extends to any point on the circle’s perimeter. All radii (plural of radius) in a given circle are equal in length. This property is crucial for understanding the characteristics of circles.
1.2. Significance of the Radius
The radius is essential because it determines the size of a circle. Knowing the radius allows you to calculate a circle’s circumference, area, and even its volume if you’re dealing with a sphere. It’s a foundational element in many geometric calculations.
1.3. Visualizing the Radius
Imagine drawing a circle. You place the compass point (the center) on the paper and rotate the pencil end to create the circle. The distance between the compass point and the pencil is the radius. No matter where you place the pencil on the circle’s edge, that distance remains constant.
1.4. Radius vs. Diameter
It’s easy to confuse the radius with the diameter. The diameter is a line segment that passes through the center of the circle, connecting two points on the circumference. The diameter is twice the length of the radius. This relationship is key to many calculations.
1.5. Why the Radius Matters
Understanding the radius is vital because it unlocks the door to understanding other properties of circles. From calculating the amount of fencing needed for a circular garden to designing gears in machinery, the radius is a fundamental measurement.
2. Essential Formulas for Calculating the Radius
Calculating the radius is straightforward with the right formulas. These formulas rely on knowing other measurements of the circle, such as its diameter, circumference, or area. Let’s explore each of these formulas in detail.
2.1. Radius from Diameter
The simplest way to find the radius is using the diameter. The diameter is always twice the radius. Therefore, the formula to find the radius when you know the diameter is:
Radius = Diameter / 2
For example, if a circle has a diameter of 10 inches, the radius is 10 / 2 = 5 inches.
2.2. Radius from Circumference
The circumference of a circle is the distance around it. The formula that relates the circumference (C) to the radius (r) is:
C = 2πr
Where π (pi) is a constant approximately equal to 3.14159. To find the radius when you know the circumference, rearrange the formula:
Radius = Circumference / (2π)
For instance, if a circle has a circumference of 25 inches, the radius is 25 / (2 * 3.14159) ≈ 3.98 inches.
2.3. Radius from Area
The area of a circle is the space enclosed within the circle. The formula that relates the area (A) to the radius (r) is:
A = πr²
To find the radius when you know the area, rearrange the formula:
Radius = √(Area / π)
For example, if a circle has an area of 50 square inches, the radius is √(50 / 3.14159) ≈ 3.99 inches.
2.4. Why These Formulas Matter
These formulas are essential tools for anyone working with circles. Whether you’re a student solving geometry problems or an engineer designing circular components, knowing how to calculate the radius from different measurements is crucial.
2.5. Practical Applications
Imagine you’re designing a circular garden and know how much space you have (the area). You can use the radius formula to determine the length of the fencing needed (related to the circumference). These formulas bridge the gap between theory and real-world applications.
3. Step-by-Step Guide: Finding the Radius of a Circle
Finding the radius of a circle is a straightforward process, provided you have the necessary information. This section offers a step-by-step guide using the three main formulas: diameter, circumference, and area.
3.1. Finding the Radius from Diameter
Step 1: Identify the Diameter
The diameter is the distance across the circle, passing through the center. If you’re given the diameter, you’re already halfway there.
Step 2: Apply the Formula
Use the formula: Radius = Diameter / 2
Step 3: Calculate
Divide the diameter by 2 to find the radius.
Example: If the diameter is 16 cm, the radius is 16 / 2 = 8 cm.
3.2. Finding the Radius from Circumference
Step 1: Identify the Circumference
The circumference is the distance around the circle.
Step 2: Apply the Formula
Use the formula: Radius = Circumference / (2π)
Step 3: Calculate
Divide the circumference by (2 * 3.14159) to find the radius.
Example: If the circumference is 31.4 inches, the radius is 31.4 / (2 * 3.14159) ≈ 5 inches.
3.3. Finding the Radius from Area
Step 1: Identify the Area
The area is the space enclosed within the circle.
Step 2: Apply the Formula
Use the formula: Radius = √(Area / π)
Step 3: Calculate
Divide the area by 3.14159, then take the square root to find the radius.
Example: If the area is 78.5 square meters, the radius is √(78.5 / 3.14159) ≈ 5 meters.
3.4. Tips for Accuracy
- Use Accurate Measurements: Ensure your diameter, circumference, or area measurements are as precise as possible.
- Use the Pi Key: If your calculator has a π key, use it for more accurate calculations.
- Double-Check Your Work: Always review your calculations to avoid simple errors.
3.5. Practice Makes Perfect
The more you practice finding the radius using these formulas, the more comfortable and confident you’ll become. Try working through various examples to solidify your understanding.
4. The Radius in Circle Equations
The radius plays a critical role in the equations that define a circle, particularly in coordinate geometry. Understanding these equations allows you to describe and analyze circles mathematically.
4.1. Standard Equation of a Circle
In the Cartesian plane, a circle with center (h, k) and radius r is described by the equation:
(x – h)² + (y – k)² = r²
This equation states that for any point (x, y) on the circle, its distance from the center (h, k) is always equal to the radius r.
4.2. Circle with Center at the Origin
A simplified version of the standard equation occurs when the center of the circle is at the origin (0, 0). In this case, the equation becomes:
x² + y² = r²
This equation is particularly useful for basic circle problems and visualizations.
4.3. Using the Equation to Find the Radius
If you’re given the equation of a circle, you can easily find the radius. Simply identify the value on the right side of the equation (r²) and take its square root.
Example: If the equation is x² + y² = 25, then r² = 25, and r = √25 = 5.
4.4. Applications in Coordinate Geometry
These equations are used extensively in coordinate geometry to solve problems involving circles. They allow you to find the distance between points on a circle, determine if a point lies inside or outside the circle, and much more.
4.5. Beyond the Basics
Understanding the radius in circle equations is a stepping stone to more advanced topics in geometry and calculus. It’s a fundamental concept that underpins many mathematical principles.
5. Radius of a Sphere: Extending the Concept
The concept of the radius extends beyond two-dimensional circles to three-dimensional spheres. Understanding the radius of a sphere is essential for calculating its volume, surface area, and other properties.
5.1. Defining the Radius of a Sphere
The radius of a sphere is the distance from the center of the sphere to any point on its surface. Just like in a circle, all radii of a given sphere are equal in length.
5.2. Importance of the Radius in Spheres
The radius is crucial for determining the size and properties of a sphere. It’s used in formulas for calculating the sphere’s volume and surface area.
5.3. Volume of a Sphere
The volume (V) of a sphere is given by the formula:
V = (4/3)πr³
Where r is the radius and π is approximately 3.14159.
5.4. Surface Area of a Sphere
The surface area (A) of a sphere is given by the formula:
A = 4πr²
Where r is the radius and π is approximately 3.14159.
5.5. Finding the Radius from Volume or Surface Area
If you know the volume or surface area of a sphere, you can rearrange these formulas to find the radius.
From Volume: r = ∛((3V) / (4π))
From Surface Area: r = √(A / (4π))
5.6. Practical Examples
- If a sphere has a volume of 100 cubic inches, its radius is ∛((3 100) / (4 3.14159)) ≈ 2.88 inches.
- If a sphere has a surface area of 200 square inches, its radius is √(200 / (4 * 3.14159)) ≈ 3.99 inches.
5.7. Real-World Applications
Understanding the radius of a sphere is important in various fields, from astronomy (calculating the size of planets) to engineering (designing spherical tanks) to medicine (analyzing the size of tumors).
6. Real-World Applications of the Radius
The radius is not just a theoretical concept; it has numerous practical applications in various fields. From engineering to design, understanding the radius is essential for solving real-world problems.
6.1. Engineering
In engineering, the radius is used to design circular components such as gears, wheels, and pipes. The precise calculation of the radius ensures that these components fit together and function correctly.
6.2. Architecture
Architects use the radius to design circular structures such as domes, arches, and circular buildings. The radius is crucial for ensuring the structural integrity and aesthetic appeal of these designs.
6.3. Manufacturing
In manufacturing, the radius is used to create circular products such as CDs, tires, and lenses. The accurate measurement of the radius is essential for ensuring the quality and consistency of these products.
6.4. Astronomy
Astronomers use the radius to measure the size of celestial bodies such as planets, stars, and moons. The radius is a fundamental parameter for understanding the physical properties of these objects.
6.5. Everyday Life
Even in everyday life, the radius plays a role. For example, when planning a circular garden, you need to know the radius to calculate the amount of fencing required. Or, when baking a round cake, the radius helps you determine the size of the cake pan.
6.6. Examples in Detail
- Designing a Gear: Engineers calculate the radius of gears to ensure they mesh properly and transmit power efficiently.
- Building a Dome: Architects use the radius to design domes that can withstand specific loads and distribute weight evenly.
- Creating a Lens: Manufacturers measure the radius of curvature of lenses to ensure they focus light correctly.
6.7. The Importance of Precision
In all these applications, precision is key. Small errors in the radius can lead to significant problems in the final product or design. Therefore, understanding and accurately calculating the radius is crucial.
7. Common Mistakes to Avoid When Calculating the Radius
Calculating the radius might seem straightforward, but there are common mistakes that can lead to incorrect results. Being aware of these pitfalls can help you avoid them and ensure accuracy in your calculations.
7.1. Confusing Radius and Diameter
One of the most common mistakes is confusing the radius with the diameter. Remember, the radius is half the diameter. Always double-check whether you’re working with the radius or the diameter before applying any formulas.
7.2. Using the Wrong Formula
Another frequent mistake is using the wrong formula. Make sure you’re using the correct formula based on the information you have (diameter, circumference, or area). Using the wrong formula will inevitably lead to an incorrect result.
7.3. Incorrectly Applying the Square Root
When calculating the radius from the area, you need to take the square root. Make sure you correctly apply the square root function. A simple error in this step can lead to a significantly wrong answer.
7.4. Forgetting to Use Pi (π)
Pi (π) is a crucial constant in circle calculations. Forgetting to include it in your formulas will result in incorrect answers. Always use π (approximately 3.14159) when calculating the radius from the circumference or area.
7.5. Rounding Errors
Rounding errors can accumulate and affect the accuracy of your results. Try to keep as many decimal places as possible during your calculations and only round the final answer.
7.6. Not Double-Checking Units
Make sure all your measurements are in the same units. If you have a mix of inches, centimeters, and meters, convert them to a single unit before performing any calculations.
7.7. Examples of Mistakes
- Using the diameter as the radius in a formula.
- Applying the area formula when you only have the circumference.
- Forgetting to take the square root after dividing the area by π.
7.8. How to Avoid Mistakes
- Double-check your work and the information you’re using.
- Write down the formula before plugging in the numbers.
- Use a calculator to avoid arithmetic errors.
- Practice regularly to become more familiar with the formulas and concepts.
8. Practical Examples and Solutions
To solidify your understanding of the radius, let’s work through some practical examples. These examples cover different scenarios and demonstrate how to apply the formulas we’ve discussed.
Example 1: Finding the Radius from the Diameter
Problem: A circle has a diameter of 24 inches. What is its radius?
Solution:
Use the formula: Radius = Diameter / 2
Radius = 24 inches / 2
Radius = 12 inches
Answer: The radius of the circle is 12 inches.
Example 2: Finding the Radius from the Circumference
Problem: A circle has a circumference of 62.8 cm. What is its radius?
Solution:
Use the formula: Radius = Circumference / (2π)
Radius = 62.8 cm / (2 * 3.14159)
Radius ≈ 10 cm
Answer: The radius of the circle is approximately 10 cm.
Example 3: Finding the Radius from the Area
Problem: A circle has an area of 154 square meters. What is its radius?
Solution:
Use the formula: Radius = √(Area / π)
Radius = √(154 square meters / 3.14159)
Radius ≈ √(49)
Radius = 7 meters
Answer: The radius of the circle is 7 meters.
Example 4: Real-World Application
Problem: You want to build a circular garden with a diameter of 8 feet. What is the radius of the garden?
Solution:
Use the formula: Radius = Diameter / 2
Radius = 8 feet / 2
Radius = 4 feet
Answer: The radius of the garden is 4 feet. This information can help you calculate the amount of fencing you need.
Example 5: Using the Circle Equation
Problem: The equation of a circle is x² + y² = 36. What is the radius of the circle?
Solution:
The equation is in the form x² + y² = r², so r² = 36.
Radius = √36
Radius = 6
Answer: The radius of the circle is 6 units.
These examples illustrate how to apply the formulas for calculating the radius in different scenarios. Practice these and similar problems to enhance your understanding and skills.
9. Frequently Asked Questions (FAQs) About the Radius of a Circle
Here are some frequently asked questions about the radius of a circle, along with detailed answers to help clarify any remaining doubts.
Q1: What is the radius of a circle?
A: The radius of a circle is the distance from the center of the circle to any point on its circumference. It is a fundamental measurement used in various geometric calculations.
Q2: How is the radius related to the diameter?
A: The diameter of a circle is twice the length of the radius. Conversely, the radius is half the length of the diameter. The relationship is expressed as: Diameter = 2 × Radius.
Q3: What is the formula for finding the radius if I know the circumference?
A: If you know the circumference (C) of a circle, you can find the radius (r) using the formula: Radius = Circumference / (2π), where π (pi) is approximately 3.14159.
Q4: How do I calculate the radius if I know the area of the circle?
A: If you know the area (A) of a circle, you can find the radius (r) using the formula: Radius = √(Area / π), where π (pi) is approximately 3.14159.
Q5: Can a circle have multiple radii?
A: Yes, a circle can have infinite radii. All radii of a given circle are equal in length, extending from the center to any point on the circumference.
Q6: What is the standard equation of a circle, and how does the radius fit into it?
A: The standard equation of a circle with center (h, k) and radius r is: (x – h)² + (y – k)² = r². In this equation, r represents the radius of the circle.
Q7: What is the radius of a sphere?
A: The radius of a sphere is the distance from the center of the sphere to any point on its surface. It is used to calculate the volume and surface area of the sphere.
Q8: How do I find the radius of a sphere if I know its volume?
A: If you know the volume (V) of a sphere, you can find the radius (r) using the formula: r = ∛((3V) / (4π)), where π (pi) is approximately 3.14159.
Q9: How do I find the radius of a sphere if I know its surface area?
A: If you know the surface area (A) of a sphere, you can find the radius (r) using the formula: r = √(A / (4π)), where π (pi) is approximately 3.14159.
Q10: Why is the radius important in real-world applications?
A: The radius is crucial in many real-world applications, including engineering, architecture, manufacturing, and astronomy. It is used to design and measure circular objects, ensuring their proper function and dimensions.
10. Need More Help? Ask Your Questions at WHAT.EDU.VN
Understanding the radius of a circle is a foundational concept in mathematics and has numerous practical applications. We’ve covered the definition, formulas, and methods for calculating the radius, along with common mistakes to avoid and real-world examples. But what if you still have questions?
At WHAT.EDU.VN, we understand that learning is a continuous process. That’s why we offer a platform where you can ask any question and get answers for free. Whether you’re struggling with a specific problem or want to deepen your understanding, our community is here to help.
10.1. Why Use WHAT.EDU.VN?
- Free: Our platform is completely free to use. Ask as many questions as you need without any cost.
- Fast Answers: Get quick and accurate answers from knowledgeable experts.
- Easy to Use: Our website is designed to be user-friendly, making it easy to ask and find answers.
- Community Support: Connect with other learners and share your knowledge.
10.2. How to Ask a Question
- Visit our website: WHAT.EDU.VN
- Create an account or log in.
- Go to the “Ask a Question” section.
- Type your question clearly and concisely.
- Provide any relevant details or context.
- Submit your question.
10.3. Contact Information
If you have any questions or need assistance, feel free to contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
10.4. Get Started Today
Don’t let your questions go unanswered. Visit WHAT.EDU.VN today and get the help you need to succeed. Our platform is designed to provide you with the knowledge and support you need to excel in your studies and beyond.
Remember, no question is too simple or too complex. We’re here to help you every step of the way. Ask your questions at what.edu.vn and unlock your full potential.