What Is The Reciprocal? It’s a fundamental concept in mathematics with wide-ranging applications. At WHAT.EDU.VN, we provide clear, easy-to-understand explanations and solutions to your math questions, completely free of charge. Uncover the secrets of reciprocals, multiplicative inverses, and more to enhance your understanding of math and related concepts.
1. Understanding the Core: What is the Reciprocal?
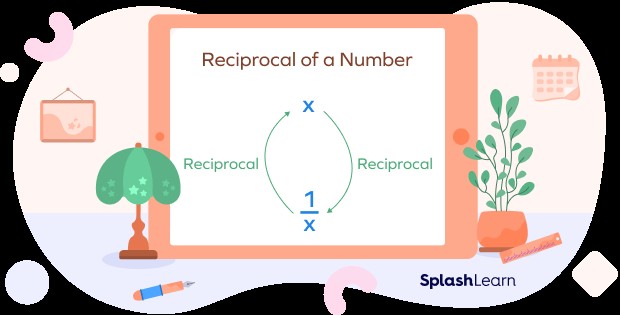
The reciprocal, also known as the multiplicative inverse, is a fundamental concept in mathematics. To put it simply, the reciprocal of a number is what you multiply that number by to get 1. This simple concept has broad implications across various mathematical operations. Let’s break down the reciprocal and its implications.
- Definition: The reciprocal of a number x is 1/x.
- Multiplicative Inverse: Reciprocal is also known as the multiplicative inverse.
- Unity: The product of a number and its reciprocal equals 1, which is called unity.
For example, the reciprocal of 5 is 1/5 because 5 (1/5) = 1. Similarly, the reciprocal of 2/3 is 3/2 because (2/3) (3/2) = 1.
2. Diving Deeper: How to Find the Reciprocal
Finding the reciprocal is a straightforward process that varies slightly depending on the type of number you’re dealing with.
- Integers: For integers, the reciprocal is simply 1 divided by that integer. For example, the reciprocal of 7 is 1/7.
- Fractions: For fractions, the reciprocal is found by swapping the numerator and the denominator. For example, the reciprocal of 3/4 is 4/3.
- Mixed Numbers: First, convert the mixed number to an improper fraction, and then find the reciprocal by swapping the numerator and denominator. For example, the mixed number 2 1/2 converts to the improper fraction 5/2, and its reciprocal is 2/5.
- Decimals: Convert the decimal to a fraction, then find the reciprocal of the fraction. For example, 0.25 is equivalent to 1/4, so its reciprocal is 4.
3. The Exception: Reciprocal of Zero
Zero is the only real number that does not have a reciprocal. Division by zero is undefined in mathematics, so 1/0 is not a valid number. Trying to find the reciprocal of zero will result in an error.
4. Reciprocals of Different Types of Numbers
Let’s examine how to find reciprocals for different types of numbers including natural numbers, negative numbers, fractions, mixed fractions and decimals.
4.1. Reciprocal of a Natural Number
The reciprocal of a natural number is one divided by the given number.
For example:
To find the reciprocal of 8,
Since the reciprocal of a number x is $frac{1}{x}$,
Therefore, the reciprocal of 8 is $frac{1}{8}$.
4.2. Reciprocal of Negative Numbers
To find the reciprocal of a negative number (-x), write the inverse of the given number with a negative sign, which is $-frac{1}{x}$.
For example:
To find the reciprocal of -5:
- Write the given number in the form of an improper fraction: -5 can be written as $frac{-5}{1}$
- Interchange the numerator and denominator values to get $frac{1}{-5}$.
- This simplifies to $-frac{1}{5}$.
4.3. Reciprocal of a Fraction
To find the reciprocal of a fraction, interchange the numerator and the denominator.
For example:
To find the reciprocal of $frac{7}{9}$:
Using the formula, reciprocal of $x = frac{1}{x}$,
Here, $x = frac{7}{9}$
Thus, $frac{1}{x} = frac{1}{frac{7}{9}} = frac{9}{7}$
Therefore, the reciprocal of the fraction $frac{7}{9}$ is $frac{9}{7}$.
4.4. Reciprocal of a Mixed Fraction
To find the reciprocal of a mixed fraction, convert it into an improper fraction first and then swap the numerator and denominator.
For example:
To find the reciprocal of $4frac{2}{3}$:
- Convert the mixed fraction into an improper fraction: $4frac{2}{3} = frac{14}{3}$.
- Flip the numerator and denominator: The reciprocal is $frac{3}{14}$.
4.5. Reciprocal of a Decimal
There are two methods to calculate the reciprocal of a decimal.
Method 1:
To find the reciprocal of 0.4:
- Write it as $frac{1}{0.4}$
- Convert to fractional form: $frac{1}{frac{4}{10}} = frac{10}{4}$
- Simplify to get $frac{5}{2}$ or 2.5.
Method 2:
To find the reciprocal of 0.75:
- Convert the decimal to a fraction: $0.75 = frac{75}{100} = frac{3}{4}$.
- Find the reciprocal of the fraction: The reciprocal of $frac{3}{4}$ is $frac{4}{3}$.
- Convert back to a decimal if needed: $frac{4}{3} approx 1.33$.
5. Applications of Reciprocals in Mathematics
Reciprocals are essential in many mathematical operations.
- Division of Fractions: Dividing by a fraction is the same as multiplying by its reciprocal.
- Solving Equations: Reciprocals are used to isolate variables in equations.
- Trigonometry: In trigonometry, reciprocal trigonometric functions like cosecant, secant, and cotangent are defined as the reciprocals of sine, cosine, and tangent, respectively.
- Calculus: Reciprocals appear in various calculus concepts, such as derivatives and integrals.
6. Real-World Applications
Beyond pure mathematics, reciprocals appear in various real-world contexts.
- Finance: Calculating rates of return or interest rates.
- Physics: Analyzing relationships between quantities like speed and time, or resistance and conductance.
- Engineering: Designing circuits or calculating ratios in mechanical systems.
7. Key Facts About Reciprocals
- The reciprocal of a reciprocal is the original number.
- The reciprocal of 1 is 1.
- The reciprocal of -1 is -1.
- Zero has no reciprocal.
- The reciprocal of a large number is a small fraction, and vice versa.
8. Solved Examples
Let’s go through some solved examples to illustrate how to find and use reciprocals.
8.1. Example 1: Finding the Reciprocal of an Integer
What is the reciprocal of 12?
Solution:
The reciprocal of 12 is $frac{1}{12}$.
8.2. Example 2: Finding the Reciprocal of a Fraction
What is the reciprocal of $frac{4}{9}$? Verify your answer.
Solution:
The reciprocal of $frac{4}{9}$ is $frac{9}{4}$.
Verification: $frac{4}{9} times frac{9}{4} = 1$
8.3. Example 3: Finding the Reciprocal of a Mixed Number
What is the reciprocal of $3frac{1}{4}$?
Solution:
First, convert $3frac{1}{4}$ to an improper fraction: $3frac{1}{4} = frac{13}{4}$.
The reciprocal of $frac{13}{4}$ is $frac{4}{13}$.
8.4. Example 4: Application in Division
Solve: $frac{2}{5} div frac{3}{4}$
Solution:
To divide by a fraction, multiply by its reciprocal:
$frac{2}{5} div frac{3}{4} = frac{2}{5} times frac{4}{3} = frac{8}{15}$
8.5. Example 5: Real-World Application
If a car travels at a speed of 60 miles per hour, what fraction of an hour does it take to travel 1 mile?
Solution:
Time = Distance / Speed
Time = 1 mile / 60 miles per hour = $frac{1}{60}$ hour
The reciprocal of the speed is the time it takes to travel one unit of distance.
9. Practice Problems
Test your understanding with these practice problems.
- Find the reciprocal of 15.
- Find the reciprocal of $frac{7}{8}$.
- Find the reciprocal of $2frac{2}{3}$.
- Solve: $frac{1}{3} div frac{5}{6}$.
- If a worker completes $frac{2}{5}$ of a job in one hour, how many hours will it take to complete the entire job?
10. Interactive Quiz
Question 1:
Which of the following statements is false?
- Reciprocal of 6 is $frac{1}{6}$.
- Reciprocal of 0 is not defined.
- Reciprocal of $-20$ is $frac{1}{20}$.
- Reciprocal of $frac{1}{11}$ is 11.
Answer: Reciprocal of -20 is $frac{1}{20}$.
(Correct Answer: Reciprocal of -20 is $-frac{1}{20}$.)
Question 2:
The reciprocal of 0 is ____.
- 1
- 100
- Not defined
Answer: Not defined
Question 3:
Which of the following is the reciprocal of $25 times 4$?
- $4 times frac{1}{25}$
- $25 times frac{1}{4}$
- $frac{1}{25 times 4}$
- 100
Answer: $frac{1}{25 times 4}$
Question 4:
Identify the reciprocal of 0.05 from the following options.
- 20
- $frac{1}{20}$
- $frac{1}{0.02}$
- -20
Answer: 20
Question 5:
If the reciprocal of an algebraic expression is $5x^3y$, then the expression will be ____.
- $-frac{1}{5x^3y}$
- $frac{1}{5x^3y}$
- $frac{1}{5xy}$
- $frac{5}{x^3y}$
Answer: $frac{1}{5x^3y}$
11. Frequently Asked Questions (FAQs)
11.1. What is the reciprocal of infinity?
The reciprocal of infinity is considered to be 0, as infinity represents an unbounded quantity, and its inverse approaches zero.
11.2. Which natural number has the same reciprocal as the number itself?
The number 1 is the only natural number that has the same reciprocal as itself because $frac{1}{1} = 1$.
11.3. What is the difference between reciprocal and inverse?
An inverse generally refers to the opposite operation, whereas a reciprocal specifically refers to the multiplicative inverse, which, when multiplied by the original number, results in 1.
11.4. What is another name for reciprocal?
Another name for reciprocal is multiplicative inverse.
11.5. What is the reciprocal of the reciprocal of a number?
The reciprocal of the reciprocal of a number is the number itself. For example, the reciprocal of 3 is $frac{1}{3}$, and the reciprocal of $frac{1}{3}$ is 3.
12. Why Understanding Reciprocals Matters
Mastering the concept of reciprocals is crucial for success in mathematics and related fields. It’s a building block for more advanced topics and a valuable tool for problem-solving in various areas of life. Whether you are a student or a professional, a solid grasp of reciprocals will serve you well.
13. Still Have Questions? Ask WHAT.EDU.VN!
Do you find math questions challenging? Are you looking for quick, free answers? Look no further! WHAT.EDU.VN is here to help.
- Ask Anything: Have a burning question about reciprocals or any other math topic? Just ask!
- Get Fast Answers: Our team of experts is ready to provide quick and accurate answers to all your questions.
- Free Help: Our services are completely free, so you can get the help you need without worrying about costs.
- Community Support: Connect with a community of learners and experts to share knowledge and get support.
Don’t struggle alone. Let WHAT.EDU.VN be your go-to resource for all your math questions.
14. Call to Action
Ready to take your math skills to the next level? Visit WHAT.EDU.VN today and ask your questions for free!
Contact us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn