The square root of 100 is a fundamental concept in mathematics. At WHAT.EDU.VN, we help you understand square root calculations, perfect squares, and mathematical operations. We provide easy solutions and help you explore mathematical concepts. Understand radical form and exponential form of square roots here.
1. Understanding the Basics of Square Roots
1.1. What Exactly Is a Square Root?
The square root of a number is a value that, when multiplied by itself, equals the original number. In simpler terms, it’s the inverse operation of squaring a number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. This can be written mathematically as √9 = 3. Understanding this fundamental relationship between squaring and finding square roots is crucial for grasping more complex mathematical concepts. Square roots are used extensively in algebra, geometry, and various fields of science and engineering. They help solve equations, calculate distances, and model physical phenomena. Whether you’re a student learning the basics or a professional applying mathematical principles, a solid understanding of square roots is essential. Need more information? Visit WHAT.EDU.VN for detailed explanations and examples.
1.2. The Square Root of 100: A Simple Explanation
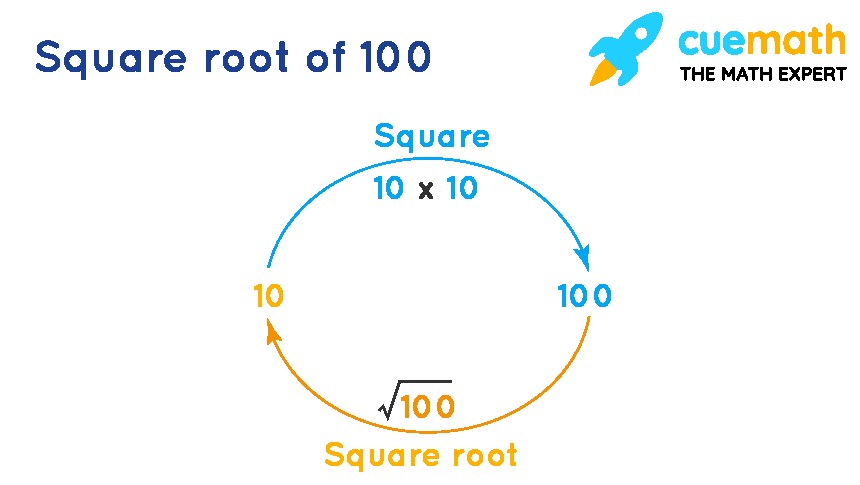
So, What Is The Square Root Of 100? It’s the number that, when multiplied by itself, gives you 100. That number is 10, because 10 x 10 = 100. Therefore, √100 = 10. This is a basic example, but it illustrates the core concept of square roots. 100 is known as a perfect square, meaning its square root is a whole number.
1.3. Why Is Understanding Square Roots Important?
Understanding square roots is essential for several reasons. Square roots are fundamental in various fields, including mathematics, physics, engineering, and computer science. They are used to solve equations, calculate distances, and analyze data. Square roots are often used to find the length of the sides of a square. This is a basic example, but it illustrates how square roots can be used to solve real-world problems. If you have questions about square roots, ask them on WHAT.EDU.VN for free. Our experts are here to help!
2. Different Ways to Express the Square Root of 100
2.1. Radical Form: √100
The radical form is the most common way to express a square root. In this form, the square root of 100 is written as √100. The symbol “√” is called the radical symbol, and it indicates that you need to find the square root of the number underneath it. This notation is universally recognized and used in mathematical expressions and equations. It’s a concise way to represent the square root operation, making it easy to incorporate into formulas and calculations. When you see √100, you immediately know that you’re looking for the number that, when multiplied by itself, equals 100. Understanding the radical form is essential for reading and interpreting mathematical texts and problems.
2.2. Exponential Form: (100)½ or (100)0.5
The exponential form is another way to represent the square root of 100. In this form, it’s written as (100)½ or (100)0.5. The exponent ½ or 0.5 indicates that you’re taking the square root of the base number, which is 100 in this case. This form is particularly useful in algebraic manipulations and calculus, where exponents are frequently used to simplify expressions and solve equations. Understanding the exponential form of square roots allows you to apply exponent rules and perform more complex calculations with ease. For example, you can use the exponential form to simplify expressions involving multiple square roots or to solve equations where square roots are raised to other powers. If you’re struggling with exponential notation, check out the resources at WHAT.EDU.VN for clear explanations and examples.
2.3. Why Are There Different Forms?
The different forms of expressing square roots (radical and exponential) exist because they serve different purposes and are useful in different contexts. The radical form (√100) is straightforward and visually represents the square root operation, making it easy to understand and use in basic calculations. The exponential form ((100)½ or (100)0.5) is more versatile and aligns with the rules of exponents, which are essential in advanced algebra and calculus. This allows for easier manipulation and simplification of complex expressions. Each form provides a unique way to approach and solve mathematical problems, catering to different levels of complexity and mathematical contexts. Knowing both forms enhances your mathematical toolkit and allows you to choose the most appropriate representation for any given situation.
3. Is the Square Root of 100 Rational or Irrational?
3.1. Understanding Rational Numbers
A rational number is a number that can be expressed as a fraction p/q, where p and q are integers and q is not equal to zero. Examples of rational numbers include 2 (which can be written as 2/1), -3/4, and 0.5 (which can be written as 1/2). Rational numbers can be represented as terminating or repeating decimals. Understanding rational numbers is fundamental in mathematics because they form the basis for many numerical operations and concepts. They are used in everyday calculations, from measuring ingredients in a recipe to calculating financial transactions. The ability to identify and work with rational numbers is essential for success in algebra, calculus, and other advanced mathematical fields. At WHAT.EDU.VN, you can find many resources to help you master working with rational numbers.
3.2. Understanding Irrational Numbers
An irrational number is a number that cannot be expressed as a fraction p/q, where p and q are integers. Irrational numbers have non-repeating, non-terminating decimal representations. Examples of irrational numbers include √2 (approximately 1.41421…) and π (approximately 3.14159…). Irrational numbers are crucial in mathematics because they represent quantities that cannot be precisely expressed using rational numbers. They appear in various areas of mathematics, including geometry (e.g., the circumference of a circle) and trigonometry (e.g., trigonometric ratios of certain angles). Recognizing and understanding irrational numbers is essential for a comprehensive grasp of mathematical concepts and their applications.
3.3. √100: Rational or Irrational?
Since √100 = 10, and 10 can be expressed as the fraction 10/1, where both 10 and 1 are integers, the square root of 100 is a rational number. This is a straightforward example that helps illustrate the difference between rational and irrational numbers. Because 10 is a whole number, it fits the definition of a rational number perfectly. Understanding this distinction is important for classifying numbers and performing accurate mathematical calculations. If you’re unsure whether a number is rational or irrational, remember to check if it can be expressed as a fraction of two integers.
4. How to Find the Square Root of 100: Two Common Methods
4.1. Method 1: Prime Factorization
Prime factorization involves breaking down a number into its prime factors. A prime factor is a number that is only divisible by 1 and itself (e.g., 2, 3, 5, 7, 11). Here’s how to find the square root of 100 using prime factorization:
- Find the prime factors of 100:
100 = 2 x 2 x 5 x 5 - Group the factors into pairs:
(2 x 2) x (5 x 5) - Take one number from each pair:
2 x 5 - Multiply the numbers together:
2 x 5 = 10
Therefore, the square root of 100 is 10. Prime factorization is a useful method for finding square roots, especially for perfect squares. It helps break down the number into manageable components, making the calculation simpler. If you’re looking for more examples or practice problems, visit WHAT.EDU.VN for comprehensive resources.
4.2. Method 2: Long Division
Long division is another method to find the square root of a number, particularly useful for larger numbers or numbers that aren’t perfect squares. Here are the steps to find the square root of 100 using long division:
- Group the digits:
Starting from the right, group the digits of 100 into pairs. In this case, it’s just ‘1 00’. - Find the largest square less than or equal to the first group:
The largest square less than or equal to 1 is 1 (1×1=1). Write 1 as the divisor and the quotient. - Subtract the square from the first group:
1 – 1 = 0. Bring down the next group (00) to make the new dividend 00. - Double the quotient and add a blank space:
Double the quotient (1) to get 2. Write ‘2_’ as the new divisor. - Find a digit to fill the blank:
Find a digit that, when placed in the blank, makes the product of the new divisor and the digit less than or equal to the new dividend (00). In this case, 0 works (20 x 0 = 0). - Write the digit in the quotient and divisor:
The new quotient is 10, and the new divisor is 20. - Subtract:
00 – 0 = 0. The remainder is 0.
Since the remainder is 0, the square root of 100 is 10. Long division can seem complicated at first, but with practice, it becomes a reliable method for finding square roots.
4.3. Which Method Is Best?
The “best” method for finding the square root of 100 depends on the situation and your personal preference. Prime factorization is excellent for perfect squares and smaller numbers because it breaks down the number into its basic components, making the process straightforward. Long division is more versatile and can be used for larger numbers and numbers that aren’t perfect squares, although it can be more complex and time-consuming. If you prefer a more conceptual approach and the number is easily factorable, prime factorization is a good choice. If you need a method that works universally, even for non-perfect squares, long division is the way to go.
5. Important Notes on Square Root of 100
5.1. The Inverse Operation
The square root operation is the inverse of squaring a number. Squaring a number means multiplying it by itself (e.g., 5² = 5 x 5 = 25). Finding the square root is the opposite: it’s finding the number that, when multiplied by itself, equals the original number (e.g., √25 = 5). Understanding this inverse relationship is crucial for solving equations and simplifying expressions. It allows you to undo the squaring operation and find the original value. This concept is widely used in algebra, calculus, and various scientific fields.
5.2. Multiple Methods Available
As we’ve discussed, there are several methods to find the square root of 100, including prime factorization, long division, and repeated subtraction. Each method offers a different approach, and the best one depends on the specific number and your personal preference. Prime factorization is great for perfect squares, while long division works for any number, even non-perfect squares. Knowing multiple methods gives you flexibility and allows you to choose the most efficient approach for each problem.
5.3. Positive and Negative Roots
While the principal square root of 100 is 10, it’s important to remember that (-10) x (-10) = 100 as well. Therefore, 100 has two square roots: 10 and -10. However, when we talk about “the” square root, we usually refer to the positive root. Being aware of both positive and negative roots is crucial in algebra and solving equations. For example, when solving the equation x² = 100, the solutions are x = 10 and x = -10.
6. Frequently Asked Questions (FAQs) on Square Root of 100
6.1. What is the square root of 100?
The square root of 100 is 10, because 10 multiplied by itself (10 x 10) equals 100.
6.2. Is the square root of 100 rational or irrational?
The square root of 100 is rational because it equals 10, which can be expressed as a fraction (10/1).
6.3. How can I find the square root of 100?
You can find the square root of 100 using prime factorization (100 = 2 x 2 x 5 x 5, so √100 = 2 x 5 = 10) or long division.
6.4. What is the square root of 100 in radical form?
In radical form, the square root of 100 is written as √100.
6.5. What is the square root of 100 in exponential form?
In exponential form, the square root of 100 is written as (100)½ or (100)0.5.
6.6. Are there two square roots of 100?
Yes, there are two square roots of 100: 10 and -10, because both 10 x 10 and (-10) x (-10) equal 100.
6.7. Why is it important to understand square roots?
Understanding square roots is important because they are fundamental in mathematics, physics, engineering, and computer science. They are used to solve equations, calculate distances, and analyze data.
6.8. Can I use a calculator to find the square root of 100?
Yes, you can use a calculator to find the square root of 100. Just enter 100 and press the square root button (√). The result will be 10.
6.9. What is a perfect square?
A perfect square is a number that is the result of squaring an integer. For example, 100 is a perfect square because it is the result of squaring 10 (10 x 10 = 100).
6.10. Where can I find more information about square roots?
You can find more information about square roots on WHAT.EDU.VN, where we provide detailed explanations, examples, and practice problems.
7. Thinking Out of the Box: Advanced Concepts
7.1. Can -10 Be Considered a Square Root of 100?
Yes, -10 can be considered a square root of 100. While 10 is the principal square root (the positive root), -10 also satisfies the condition that its square equals 100, since (-10) x (-10) = 100. Both 10 and -10 are valid square roots of 100.
7.2. Forming a Quadratic Equation with Roots 100 and -100
To determine a quadratic equation whose roots are 100 and -100, we can use the fact that if a quadratic equation has roots r and s, it can be written in the form:
x² – (r + s)x + rs = 0
In this case, r = 100 and s = -100. Substituting these values into the equation, we get:
x² – (100 + (-100))x + (100 x -100) = 0
x² – (0)x + (-10000) = 0
x² – 10000 = 0
Therefore, the quadratic equation whose roots are 100 and -100 is x² – 10000 = 0.
7.3. Real-World Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous practical applications in various fields. In physics, they are used to calculate velocities and accelerations. For instance, the velocity of an object can be determined using the formula v = √2gh, where g is the acceleration due to gravity and h is the height from which the object falls. In engineering, square roots are essential for designing structures, calculating stress and strain, and determining the stability of buildings and bridges. In computer graphics, they are used for calculating distances and creating realistic 3D models. The Pythagorean theorem, which involves square roots, is used extensively in navigation and surveying to determine distances and angles. Understanding these real-world applications helps illustrate the importance of square roots and their relevance in solving practical problems.
8. Need More Help? Ask on WHAT.EDU.VN!
Are you still struggling with square roots or have other math questions? Don’t worry! WHAT.EDU.VN is here to help. We offer a free question-and-answer platform where you can ask any question and get expert answers quickly. Whether you’re a student, a professional, or just curious, our community is ready to assist you. Stop struggling and start learning today. Post your questions on WHAT.EDU.VN and get the answers you need to succeed.
Navigating the world of math can be challenging, but with the right resources and support, you can overcome any obstacle. WHAT.EDU.VN is dedicated to providing you with the tools and knowledge you need to excel. From basic concepts to advanced topics, we’ve got you covered. Join our community today and experience the power of collaborative learning.
Don’t let math intimidate you. Embrace the challenge and discover the beauty and power of mathematics with WHAT.EDU.VN. We’re here to help you every step of the way.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Ask your question now on what.edu.vn and get a free answer!