The square root of 5, often denoted as √5, is a fundamental concept in mathematics with wide-ranging applications. Discover the essence of square root of five, explore its significance, and learn how to calculate it accurately with WHAT.EDU.VN. Delve into rational approximations, mathematical properties, and real-world uses. Uncover the value, radical form, and exponent form today.
1. What Is the Square Root of 5? A Comprehensive Guide
The square root of a number ‘x’ is a value ‘y’ that, when multiplied by itself, equals ‘x’. In mathematical terms, if y² = x, then y is the square root of x. The square root of 5 is a real number that, when multiplied by itself, gives 5.
Mathematically, it is expressed as √5. It’s the positive solution to the equation x² = 5.
Understanding the Basics
- Definition: The square root of 5 is a number that, when multiplied by itself, equals 5.
- Symbol: √5
- Approximate Value: 2.236
- Nature: Irrational
 Square root of 5 representation
Square root of 5 representation
Square Root of 5: Numerical Representation
The square root of 5 is approximately 2.236. This means that 2.236 multiplied by itself is approximately equal to 5. This value is essential in many mathematical and scientific calculations.
Square Root of 5: Radical and Exponent Forms
The square root of 5 can be represented in two common forms:
- Radical Form: √5
- Exponent Form: 5^(1/2) or 5^0.5
These forms are interchangeable and are used in various mathematical contexts.
Why is Square Root of 5 Important?
The square root of 5 appears in numerous areas of mathematics, physics, and engineering. It is a fundamental constant in various calculations and models.
How to Calculate the Square Root of 5?
There are several methods to calculate the square root of 5. The most common methods include:
- Long Division Method
- Babylonian Method
- Using a Calculator
We will explore these methods in detail later in this article.
Square Root of 5: Real-World Applications
The square root of 5 is not just a theoretical concept. It has numerous real-world applications, including:
- Geometry: Calculating the length of diagonals in rectangles and squares.
- Physics: Determining the period of a pendulum.
- Engineering: Designing structures and calculating stress and strain.
- Finance: Modeling growth rates and returns on investment.
2. Is the Square Root of 5 Rational or Irrational?
One of the fundamental questions about the square root of 5 is whether it is a rational or irrational number. Understanding this distinction is crucial in mathematics.
Defining Rational and Irrational Numbers
- Rational Number: A number that can be expressed as a fraction p/q, where p and q are integers and q ≠ 0.
- Irrational Number: A number that cannot be expressed as a fraction p/q, where p and q are integers.
Proof that √5 is Irrational
To prove that √5 is irrational, we can use a proof by contradiction.
- Assume that √5 is rational.
- Then, √5 = p/q, where p and q are integers with no common factors (i.e., the fraction is in its simplest form).
- Squaring both sides, we get 5 = p²/q².
- This implies that p² = 5q².
- Since p² is a multiple of 5, p must also be a multiple of 5. Therefore, p = 5k for some integer k.
- Substituting p = 5k into the equation p² = 5q², we get (5k)² = 5q², which simplifies to 25k² = 5q².
- Dividing both sides by 5, we get 5k² = q².
- This implies that q² is a multiple of 5, and therefore, q must also be a multiple of 5.
- However, we assumed that p and q have no common factors. This contradicts our assumption that both p and q are multiples of 5.
- Therefore, our initial assumption that √5 is rational must be false.
Conclusion: √5 is Irrational
Since our assumption that √5 is rational leads to a contradiction, we can conclude that √5 is indeed an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
Implications of √5 Being Irrational
The irrationality of √5 has several implications:
- Its decimal representation goes on infinitely without repeating.
- It cannot be expressed as a ratio of two integers.
- It is a real number but not a rational number.
Examples of Rational and Irrational Numbers
| Type | Number | Explanation |
|---|---|---|
| Rational | 2 | Can be expressed as 2/1 |
| Rational | 0.5 | Can be expressed as 1/2 |
| Rational | 0.333… | Can be expressed as 1/3 |
| Irrational | √2 | Cannot be expressed as a simple fraction; decimal representation is infinite |
| Irrational | π | Cannot be expressed as a simple fraction; decimal representation is infinite |
| Irrational | √5 | Cannot be expressed as a simple fraction; decimal representation is infinite |
3. How to Find the Square Root of 5? Methods Explained
Calculating the square root of 5 can be done using various methods. Here, we will explore three common methods:
- Long Division Method
- Babylonian Method
- Using a Calculator
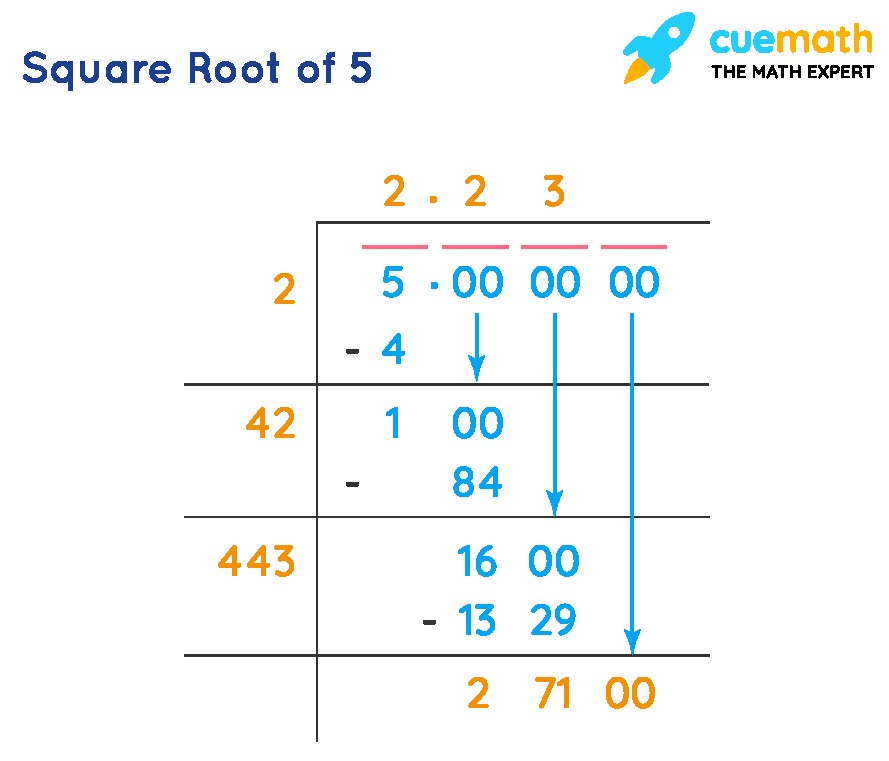
Method 1: Long Division Method
The long division method is a manual way to find the square root of a number. Here are the steps to find the square root of 5 using this method:
- Set up the division: Write 5.000000 (add pairs of zeros after the decimal) inside the division symbol.
- Find the largest square: Find the largest integer whose square is less than or equal to 5. In this case, it is 2 (since 2² = 4).
- Divide and subtract: Write 2 as the quotient and subtract 4 from 5, leaving a remainder of 1.
- Bring down the next pair of zeros: Bring down the next pair of zeros (00) to the remainder, making it 100.
- Double the quotient: Double the current quotient (2) to get 4.
- Find the next digit: Find a digit ‘x’ such that (4x) x is less than or equal to 100. In this case, x = 2, so (42) 2 = 84.
- Subtract again: Subtract 84 from 100, leaving a remainder of 16.
- Repeat the process: Bring down the next pair of zeros (00) to the remainder, making it 1600. Double the current quotient (22) to get 44. Find a digit ‘x’ such that (44x) x is less than or equal to 1600. In this case, x = 3, so (443) 3 = 1329.
- Continue the iterations: Continue this process to get more decimal places.
Following these steps, you will find that √5 ≈ 2.236.
Method 2: Babylonian Method
The Babylonian method, also known as Heron’s method, is an iterative method for approximating the square root of a number. Here are the steps:
- Start with an initial guess: Choose an initial guess for the square root of 5. A reasonable guess is 2.
- Iterate: Use the formula: x_(n+1) = 0.5 * (x_n + 5/x_n), where xn is the current guess and x(n+1) is the next guess.
- Repeat: Repeat the iteration until the value converges to a stable approximation.
Let’s perform a few iterations:
- Iteration 1: x_1 = 0.5 * (2 + 5/2) = 2.25
- Iteration 2: x_2 = 0.5 * (2.25 + 5/2.25) = 2.23611
- Iteration 3: x_3 = 0.5 * (2.23611 + 5/2.23611) = 2.236067977
After a few iterations, the value converges to approximately 2.236.
Method 3: Using a Calculator
The simplest way to find the square root of 5 is by using a calculator. Simply enter 5 and press the square root button (√). The calculator will display the approximate value of √5, which is 2.236.
Comparison of Methods
| Method | Accuracy | Complexity | Tools Required |
|---|---|---|---|
| Long Division | High | High | Paper, Pencil |
| Babylonian Method | High | Medium | Calculator |
| Using a Calculator | High | Low | Calculator |
4. Properties of the Square Root of 5
Understanding the properties of the square root of 5 can provide deeper insights into its behavior and applications in mathematics.
Basic Properties
- Irrationality: As proven earlier, √5 is an irrational number.
- Real Number: √5 is a real number, meaning it can be represented on the number line.
- Positive Value: By convention, √5 refers to the positive square root of 5.
- Approximation: √5 ≈ 2.236
Mathematical Properties
- Squaring: (√5)² = 5
- Multiplication: √5 * √5 = 5
- Division: √5 / √5 = 1
- Addition and Subtraction: √5 + √5 = 2√5, √5 – √5 = 0
Algebraic Properties
- Simplification: √20 = √(4 * 5) = 2√5
- Rationalizing the Denominator: To rationalize a denominator containing √5, multiply both the numerator and denominator by √5. For example, 1/√5 = (1/√5) * (√5/√5) = √5/5.
- Equations: If x² = 5, then x = ±√5.
Geometric Properties
- Golden Ratio: The golden ratio, φ, is related to √5 by the formula: φ = (1 + √5) / 2 ≈ 1.618.
- Pentagons: √5 appears in the formulas for the diagonals and areas of regular pentagons.
Table of Properties
| Property | Description | Example |
|---|---|---|
| Irrationality | √5 cannot be expressed as a ratio of two integers. | √5 ≈ 2.236 (non-repeating, non-terminating) |
| Real Number | √5 can be represented on the number line. | √5 is between 2 and 3 |
| Squaring | Squaring √5 results in 5. | (√5)² = 5 |
| Multiplication | Multiplying √5 by itself results in 5. | √5 * √5 = 5 |
| Simplification | √5 can be used to simplify other square roots. | √20 = 2√5 |
| Golden Ratio | √5 is used in the formula for the golden ratio. | φ = (1 + √5) / 2 |
5. Applications of Square Root of 5 in Various Fields
The square root of 5 is not just a mathematical curiosity; it has significant applications in various fields, including mathematics, physics, engineering, and computer science.
Mathematics
- Golden Ratio: As mentioned earlier, √5 is integral to the golden ratio (φ), which is approximately 1.618. The golden ratio appears in geometry, art, and architecture.
- Geometry: In regular pentagons, the ratio of a diagonal to a side is the golden ratio, which involves √5.
- Number Theory: √5 is used in various number theory problems, particularly in quadratic fields and Diophantine equations.
Physics
- Pendulum Motion: In simple harmonic motion, the period of a pendulum can involve square roots, and √5 can appear in calculations related to pendulum lengths or gravitational constants.
- Special Relativity: √5 might appear in calculations involving spacetime intervals or energy-momentum relationships in advanced physics contexts.
Engineering
- Structural Engineering: √5 can be used in calculations for structural stability and stress analysis, particularly in structures involving pentagonal or hexagonal geometries.
- Electrical Engineering: In circuit analysis, √5 can appear in calculations involving impedance or resonance frequencies in certain types of circuits.
Computer Science
- Algorithms: √5 can appear in the analysis of certain algorithms, particularly those involving geometric or numerical computations.
- Graphics: In computer graphics, √5 can be used in calculations for geometric transformations and rendering algorithms.
Finance
- Financial Modeling: Although less direct, √5 can indirectly appear in financial models that use geometric progressions or growth rates related to the golden ratio.
Examples in Specific Applications
- Geometry: Calculating the diagonal of a rectangle with sides in the golden ratio involves √5.
- Physics: Determining the period of a pendulum with specific length and gravitational acceleration can indirectly involve √5.
- Engineering: Designing a bridge with pentagonal supports might require calculations involving √5 for structural integrity.
Table of Applications
| Field | Application | Example |
|---|---|---|
| Mathematics | Golden Ratio | Calculating proportions in art and architecture |
| Geometry | Regular Pentagons | Finding the ratio of a diagonal to a side in a pentagon |
| Physics | Pendulum Motion | Calculating the period of a pendulum |
| Engineering | Structural Analysis | Analyzing stress in structures with pentagonal elements |
| Computer Science | Algorithm Analysis | Analyzing the complexity of geometric algorithms |
| Finance | Financial Modeling | Indirectly in models using geometric progressions |
6. Square Root of 5 and the Golden Ratio
The golden ratio, often denoted by the Greek letter φ (phi), is an irrational number approximately equal to 1.6180339887. It is deeply connected to the square root of 5 and appears in various areas of mathematics, art, architecture, and nature.
The Golden Ratio Formula
The golden ratio can be defined as:
φ = (1 + √5) / 2
This formula explicitly includes the square root of 5, highlighting its importance in determining the value of the golden ratio.
Properties of the Golden Ratio
- Irrationality: Like √5, the golden ratio is an irrational number, meaning its decimal representation is non-repeating and non-terminating.
- Self-Similarity: The golden ratio exhibits self-similarity, meaning that it appears in nested patterns. For example, dividing a line segment into two parts such that the ratio of the whole segment to the longer part is the same as the ratio of the longer part to the shorter part yields the golden ratio.
- Mathematical Significance: The golden ratio is related to the Fibonacci sequence, where each number is the sum of the two preceding ones (e.g., 1, 1, 2, 3, 5, 8, 13, …). The ratio of consecutive Fibonacci numbers approaches the golden ratio as the sequence progresses.
Applications of the Golden Ratio
- Geometry: The golden ratio appears in the construction of regular pentagons, decagons, and dodecahedrons. The ratio of a diagonal to a side in a regular pentagon is the golden ratio.
- Art and Architecture: Many artists and architects have used the golden ratio to create aesthetically pleasing designs. Examples include the Parthenon in Athens and works by Leonardo da Vinci.
- Nature: The golden ratio is found in various natural phenomena, such as the arrangement of leaves on a stem, the spirals of seashells, and the branching of trees.
- Finance: The golden ratio is sometimes used in technical analysis to predict potential levels of support and resistance in financial markets.
Examples of the Golden Ratio in Art and Architecture
- The Parthenon: The dimensions of the Parthenon in Athens are said to approximate the golden ratio, contributing to its visual harmony.
- Leonardo da Vinci’s Works: Leonardo da Vinci incorporated the golden ratio into many of his paintings, including the Mona Lisa and The Last Supper.
- Modern Architecture: Many modern architects use the golden ratio to design buildings and structures that are visually appealing.
Table of Connections
| Aspect | Connection to √5 | Application |
|---|---|---|
| Formula | φ = (1 + √5) / 2 | Calculating the exact value of the golden ratio |
| Geometry | Regular Pentagons | Determining the ratio of a diagonal to a side in a pentagon |
| Art and Architecture | Aesthetic Proportions | Creating visually pleasing designs |
| Nature | Natural Patterns | Explaining the arrangement of leaves, spirals of seashells, and branching of trees |
| Finance | Technical Analysis | Predicting potential levels of support and resistance in financial markets |
7. Approximating the Square Root of 5: Methods and Accuracy
Approximating the square root of 5 is often necessary when a precise value is not required or when performing calculations manually. Here, we will discuss several methods for approximating √5 and their respective accuracy.
1. Integer Approximation
The simplest approximation is to identify the two perfect squares that 5 lies between.
- 2² = 4
- 3² = 9
Since 5 is between 4 and 9, √5 is between 2 and 3. As 5 is closer to 4 than to 9, √5 is closer to 2 than to 3.
2. Linear Interpolation
Linear interpolation involves estimating the value based on the assumption that the function behaves linearly between two known points.
Using the values from the integer approximation:
- √4 = 2
- √9 = 3
Since 5 is 1/5 of the way between 4 and 9:
√5 ≈ 2 + (1/5) * (3 – 2) = 2 + 0.2 = 2.2
3. Babylonian Method (Heron’s Method)
As discussed earlier, the Babylonian method is an iterative approach:
- Start with an initial guess: x_0 = 2
- Iterate: x_(n+1) = 0.5 * (x_n + 5/x_n)
- Iteration 1: x_1 = 0.5 * (2 + 5/2) = 2.25
- Iteration 2: x_2 = 0.5 * (2.25 + 5/2.25) ≈ 2.23611
- Iteration 3: x_3 = 0.5 * (2.23611 + 5/2.23611) ≈ 2.236067977
4. Taylor Series Expansion
The Taylor series expansion can be used to approximate √5. The Taylor series for √(a + x) around a = 4 is:
√(4 + x) ≈ √4 + (x / (2√4)) – (x² / (8(√4)³)) + …
For √5, x = 1:
√5 ≈ 2 + (1 / (2 2)) – (1 / (8 2³)) + … ≈ 2 + 0.25 – 0.015625 ≈ 2.234375
5. Calculator Approximation
Using a calculator, √5 ≈ 2.236067977
Comparison of Accuracy
| Method | Approximation | Accuracy (vs. 2.236067977) |
|---|---|---|
| Integer Approximation | 2 | Low |
| Linear Interpolation | 2.2 | Medium |
| Babylonian Method (2 iterations) | 2.23611 | High |
| Taylor Series | 2.234375 | High |
| Calculator | 2.236067977 | Very High |
Conclusion
The accuracy of the approximation depends on the method used. For quick estimations, linear interpolation or integer approximation may suffice. For more accurate results, the Babylonian method or Taylor series expansion are preferable. For the highest accuracy, a calculator is the best option.
8. The Square Root of 5 in Geometry: Pentagons and More
The square root of 5 plays a significant role in geometry, particularly in the study of pentagons and other related shapes. Its presence is closely tied to the golden ratio, which appears in various geometric constructions.
1. Regular Pentagons
A regular pentagon is a polygon with five equal sides and five equal angles. The diagonals of a regular pentagon form a pentagram, and the ratio of a diagonal to a side is the golden ratio (φ).
- Diagonal to Side Ratio: In a regular pentagon, if the side length is ‘a’, the diagonal length ‘d’ is given by d = a * φ, where φ = (1 + √5) / 2.
2. Golden Triangles
Golden triangles are isosceles triangles with angles in the ratio 36:72:72 or 72:36:72. These triangles are closely related to the golden ratio and regular pentagons.
- Acute Golden Triangle: Has angles 36°, 72°, and 72°. The ratio of the longer side to the shorter side is the golden ratio.
- Obtuse Golden Triangle: Has angles 72°, 36°, and 72°. The ratio of the shorter side to the longer side is the golden ratio.
3. Decagons
A decagon is a polygon with ten sides. Regular decagons can be constructed using the golden ratio and, therefore, involve √5.
- Relationship to Pentagons: A regular decagon can be constructed by extending the sides of a regular pentagon. The vertices of the pentagon are also vertices of the decagon.
4. Dodecahedrons
A dodecahedron is a polyhedron with twelve faces, each of which is a regular pentagon. The geometry of a dodecahedron is intimately linked to the golden ratio and √5.
- Construction: Dodecahedrons can be constructed using golden rectangles, which have sides in the ratio of the golden ratio.
5. Icosahedrons
An icosahedron is a polyhedron with twenty faces, each of which is an equilateral triangle. While the direct relationship is less obvious, the icosahedron’s symmetry and geometry are related to the golden ratio and, consequently, √5.
Geometric Formulas Involving √5
- Area of a Regular Pentagon:
- If ‘a’ is the side length, the area A = (a² / 4) * √(25 + 10√5).
- Diagonal of a Regular Pentagon:
- If ‘a’ is the side length, the diagonal d = a * (1 + √5) / 2.
- Height of a Golden Triangle:
- In an acute golden triangle with base ‘a’, the height h = (a / 2) * √(1 + (2/√5)).
Table of Geometric Relationships
| Shape | Relationship to √5 | Application |
|---|---|---|
| Regular Pentagon | Diagonal to side ratio is (1 + √5) / 2 | Constructing pentagons, calculating areas and diagonals |
| Golden Triangles | Side ratios involve the golden ratio, related to √5 | Analyzing triangles with angles in 36:72:72 ratio |
| Decagons | Construction and properties are related to the golden ratio and √5 | Constructing decagons, understanding their geometry |
| Dodecahedrons | Faces are regular pentagons; geometry linked to golden ratio and √5 | Analyzing polyhedra with pentagonal faces |
| Icosahedrons | Symmetry and geometry indirectly related to the golden ratio and √5 | Understanding polyhedra with triangular faces |
9. Challenging Questions and Problems Involving the Square Root of 5
Testing your understanding with challenging questions can solidify your knowledge of the square root of 5 and its applications.
Question 1: Simplifying Expressions
Simplify the expression: (3 + √5) * (3 – √5)
Solution:
This is a difference of squares: (a + b) * (a – b) = a² – b²
(3 + √5) * (3 – √5) = 3² – (√5)² = 9 – 5 = 4
Question 2: Rationalizing the Denominator
Rationalize the denominator of the fraction: 2 / (1 + √5)
Solution:
Multiply the numerator and denominator by the conjugate of the denominator:
[2 / (1 + √5)] [(1 – √5) / (1 – √5)] = [2 (1 – √5)] / (1² – (√5)²) = [2 – 2√5] / (1 – 5) = [2 – 2√5] / (-4) = (√5 – 1) / 2
Question 3: Geometric Application
A regular pentagon has a side length of 4 units. Find the length of its diagonal.
Solution:
The diagonal of a regular pentagon is given by d = a * φ, where a is the side length and φ = (1 + √5) / 2.
d = 4 [(1 + √5) / 2] = 2 (1 + √5) ≈ 2 (1 + 2.236) = 2 3.236 ≈ 6.472 units
Question 4: Quadratic Equations
Solve the quadratic equation: x² – 2x – 4 = 0
Solution:
Use the quadratic formula: x = [-b ± √(b² – 4ac)] / (2a)
In this case, a = 1, b = -2, and c = -4.
x = [2 ± √((-2)² – 4 1 -4)] / (2 * 1) = [2 ± √(4 + 16)] / 2 = [2 ± √20] / 2 = [2 ± 2√5] / 2 = 1 ± √5
The solutions are x = 1 + √5 and x = 1 – √5.
Question 5: Fibonacci Sequence
The Fibonacci sequence is defined as F(n) = F(n-1) + F(n-2), with F(0) = 0 and F(1) = 1. Show that the limit of the ratio of consecutive Fibonacci numbers approaches the golden ratio.
Solution:
Let φ be the golden ratio. Then, as n approaches infinity, F(n+1) / F(n) approaches φ, where φ = (1 + √5) / 2.
Table of Problems and Solutions
| Question | Solution | Category |
|---|---|---|
| Simplify (3 + √5) * (3 – √5) | 4 | Algebra |
| Rationalize 2 / (1 + √5) | (√5 – 1) / 2 | Algebra |
| Diagonal of a pentagon (side = 4) | 6.472 units | Geometry |
| Solve x² – 2x – 4 = 0 | x = 1 ± √5 | Quadratic Equation |
| Fibonacci sequence limit | F(n+1) / F(n) approaches (1 + √5) / 2 as n approaches infinity | Number Theory |
10. Important Notes on the Square Root of 5
To wrap up our comprehensive guide, here are some important notes and key takeaways regarding the square root of 5.
Key Takeaways
- Definition: The square root of 5 is a number that, when multiplied by itself, equals 5.
- Irrationality: √5 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
- Approximation: √5 ≈ 2.236
- Golden Ratio: √5 is a fundamental component of the golden ratio (φ), which is approximately 1.618.
- Applications: √5 appears in various fields, including mathematics, physics, engineering, and art.
- Methods of Calculation: The square root of 5 can be calculated using methods such as long division, the Babylonian method, and calculators.
Common Misconceptions
- √5 is a rational number: It is crucial to remember that √5 is irrational.
- √5 has a simple decimal representation: The decimal representation of √5 is infinite and non-repeating.
- Approximations are exact: Approximations of √5 are not exact; they are only close estimates.
Tips for Remembering
- Associate with the Golden Ratio: Remembering that √5 is part of the golden ratio can help recall its significance.
- Use Mnemonics: Create a mnemonic to remember the first few digits of √5 (e.g., “Two point Two, Three, Six”).
- Practice: Regularly practice calculations and problems involving √5 to reinforce your understanding.
Further Exploration
- Golden Ratio in Art and Architecture: Explore how the golden ratio, and thus √5, is used in famous artworks and buildings.
- Fibonacci Sequence: Investigate the relationship between the Fibonacci sequence and the golden ratio.
- Geometric Constructions: Practice constructing regular pentagons and decagons using the golden ratio.
Final Thoughts
The square root of 5 is a fascinating and important number with far-reaching implications. By understanding its properties, applications, and connections to other mathematical concepts, you can gain a deeper appreciation for the beauty and complexity of mathematics.
Need more help with understanding mathematical concepts or solving complex problems? Visit WHAT.EDU.VN for free, expert answers to all your questions. Our community of knowledgeable experts is ready to assist you with clear, concise explanations and step-by-step guidance. Don’t struggle alone – ask your question on WHAT.EDU.VN today and get the answers you need quickly and easily.
Address: 888 Question City Plaza, Seattle, WA 98101, United States. Whatsapp: +1 (206) 555-7890. Website: what.edu.vn
FAQ on Square Root of 5
| Question | Answer |
|---|---|
| What Is The Square Root Of 5? | The square root of 5 is a number that, when multiplied by itself, equals 5. It is approximately 2.236. |
| Is the square root of 5 rational or irrational? | The square root of 5 is an irrational number. It cannot be expressed as a simple fraction, and its decimal representation is non-repeating and non-terminating. |
| How do you calculate the square root of 5? | The square root of 5 can be calculated using methods such as long division, the Babylonian method, or a calculator. |
| What is the golden ratio, and how is it related to the square root of 5? | The golden ratio (φ) is an irrational number approximately equal to 1.618. It is related to the square root of 5 by the formula φ = (1 + √5) / 2. |
| What are some applications of the square root of 5? | The square root of 5 appears in various fields, including mathematics (geometry, number theory), physics (pendulum motion), engineering (structural analysis), and art (the golden ratio in design). |
| How can you approximate the square root of 5? | You can approximate the square root of 5 using methods such as integer approximation, linear interpolation, or iterative methods like the Babylonian method. |
| What is the value of √5 up to five decimal places? | The value of √5 up to five decimal places is 2.23607. |
| Can the square root of 5 be expressed as a fraction? | No, the square root of 5 cannot be expressed as a fraction of two integers. This is because it is an irrational number. |
| Where does the square root of 5 appear in geometry? | The square root of 5 appears in the geometry of regular pentagons, golden triangles, decagons, dodecahedrons, and icosahedrons. It is particularly significant in the ratios and proportions within these shapes. |
| What is the importance of understanding the square root of 5? | Understanding the square root of 5 is important because it is a fundamental mathematical concept with wide-ranging applications in various fields. It also provides a deeper understanding of irrational numbers and their significance in mathematics and science. |