What Is The Square Root Of 81? Discover the answer and explore methods to calculate it accurately with WHAT.EDU.VN. This guide simplifies the concept and provides easy-to-understand explanations, ensuring you grasp the fundamentals of square roots, radical form, and perfect squares. Enhance your math skills today.
1. Understanding the Basics of the Square Root of 81
The square root of 81 is a value that, when multiplied by itself, equals 81. In simpler terms, we’re looking for a number that, when squared, gives us 81. This concept is fundamental in mathematics and has various applications across different fields. Understanding it can significantly improve your problem-solving skills.
The square root of 81 is symbolically represented as √81. This notation indicates that we are seeking the principal square root, which is the non-negative value. Therefore:
√81 = Number × Number = 81
To find the square root of 81, we look for a number that, when multiplied by itself, yields 81. In this case, that number is 9.
9 x 9 = 81
Thus:
√81 = 9
However, it’s crucial to remember that both positive and negative numbers can result in a positive square when multiplied by themselves. Therefore, while 9 is the principal square root, -9 is also a square root of 81, since:
(-9) x (-9) = 81
So, the square root of 81 can be expressed as ±9.
Here’s a quick summary:
| Aspect | Value |
|---|---|
| Square Root of 81 | 9 |
| Negative Square Root | -9 |
| Principal Square Root | 9 |
| Radical Form of Square Root of 81 | √81 |
Understanding these basics is vital before moving on to methods of calculation. Let’s delve deeper into the implications and practical uses of this knowledge. If you have any questions, remember that WHAT.EDU.VN provides a platform to ask and get answers for free. Feel free to reach out to us at 888 Question City Plaza, Seattle, WA 98101, United States or contact us via Whatsapp at +1 (206) 555-7890. You can also visit our website at WHAT.EDU.VN for more information.
2. Exploring the Square Root of 81 in Radical Form
The simplest radical form of the square root of 81 is √81. This form represents the exact value of the square root before any simplification. Understanding radical form is crucial for dealing with more complex mathematical expressions.
Radical form is a way to express numbers using a radical symbol (√), which indicates the root of a number. In the case of the square root of 81, the radical form is simply √81. This notation is important because it represents the precise, unsimplified value of the square root.
Key points about radical form:
- Exact Representation: Radical form provides an exact representation of the number without approximation.
- Simplification: It is often the first step in simplifying square roots before finding a whole number or decimal equivalent.
- Mathematical Operations: Radical form is used extensively in algebraic and calculus operations.
When we express the square root of 81 in radical form, we write √81. To simplify this, we look for a perfect square that divides 81. In this case, 81 is itself a perfect square.
Since 9 × 9 = 81, we can simplify √81 to 9.
Therefore, the simplest radical form of the square root of 81 is √81, which simplifies to 9.
Here’s a summary:
| Aspect | Value |
|---|---|
| Radical Form | √81 |
| Simplified Radical Form | 9 |
Radical form is essential for various mathematical contexts, including geometry, algebra, and calculus. Understanding it ensures that you can accurately manipulate and simplify mathematical expressions. If you’re struggling with any math concepts, remember that WHAT.EDU.VN offers a platform to ask questions and get free answers. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States or via Whatsapp at +1 (206) 555-7890. Visit our website at WHAT.EDU.VN for more details.
3. Calculating the Square Root of 81 Using Prime Factorization
Prime factorization is a method of finding the square root of a number by breaking it down into its prime factors. For 81, this method is straightforward and provides a clear understanding of why 9 is the square root.
To calculate the square root of 81 using prime factorization, follow these steps:
-
Find the Prime Factors of 81:
- Start by dividing 81 by the smallest prime number, which is 2. Since 81 is not divisible by 2, move to the next prime number, 3.
- 81 ÷ 3 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So, the prime factors of 81 are 3 × 3 × 3 × 3.
-
Group the Prime Factors into Pairs:
- √81 = √(3 × 3 × 3 × 3)
- √81 = √((3 × 3) × (3 × 3))
-
Simplify the Expression:
- √81 = √(3^2 × 3^2)
- √81 = 3 × 3
- √81 = 9
Therefore, the square root of 81, calculated using prime factorization, is 9.
Key points about prime factorization:
- Breaks Down Complex Numbers: Simplifies the process of finding square roots for larger numbers.
- Identifies Perfect Squares: Helps identify whether a number is a perfect square by ensuring all factors can be paired.
- Fundamental in Number Theory: Prime factorization is a fundamental concept in number theory and is used in various mathematical applications.
Here’s a summary:
| Step | Description | Result |
|---|---|---|
| 1. Prime Factorization | 81 = 3 × 3 × 3 × 3 | 3 × 3 × 3 × 3 |
| 2. Grouping | √81 = √((3 × 3) × (3 × 3)) | √((3 × 3) × (3 × 3)) |
| 3. Simplification | √81 = 3 × 3 | 9 |
Using prime factorization, we clearly see that √81 = 9. This method provides a solid foundation for understanding square roots. If you have further questions or need help with other math problems, visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also reach us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for more information and assistance.
4. Repeated Subtraction Method for Finding the Square Root of 81
The repeated subtraction method is an elementary technique for finding the square root of a perfect square by successively subtracting odd numbers until you reach zero. The number of subtractions performed gives you the square root.
To find the square root of 81 using the repeated subtraction method:
- Start with the Number: Begin with 81.
- Subtract Successive Odd Numbers: Subtract consecutive odd numbers (1, 3, 5, 7, …) from 81 until you reach 0.
- 81 – 1 = 80
- 80 – 3 = 77
- 77 – 5 = 72
- 72 – 7 = 65
- 65 – 9 = 56
- 56 – 11 = 45
- 45 – 13 = 32
- 32 – 15 = 17
- 17 – 17 = 0
- Count the Number of Subtractions: Count how many times you subtracted an odd number to reach 0. In this case, you subtracted 9 times.
Therefore, the square root of 81, using the repeated subtraction method, is 9.
Key points about the repeated subtraction method:
- Simple and Intuitive: Easy to understand and perform, especially for small perfect squares.
- Illustrates the Concept of Square Roots: Helps visualize the relationship between square roots and odd numbers.
- Limited Practical Use: Not efficient for large numbers or non-perfect squares.
Here’s a summary:
| Subtraction | Calculation | Result |
|---|---|---|
| 1 | 81 – 1 | 80 |
| 2 | 80 – 3 | 77 |
| 3 | 77 – 5 | 72 |
| 4 | 72 – 7 | 65 |
| 5 | 65 – 9 | 56 |
| 6 | 56 – 11 | 45 |
| 7 | 45 – 13 | 32 |
| 8 | 32 – 15 | 17 |
| 9 | 17 – 17 | 0 |
The repeated subtraction method clearly shows that the square root of 81 is 9. If you need further clarification or assistance with math problems, visit WHAT.EDU.VN. Our address is 888 Question City Plaza, Seattle, WA 98101, United States. You can also contact us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for more help.
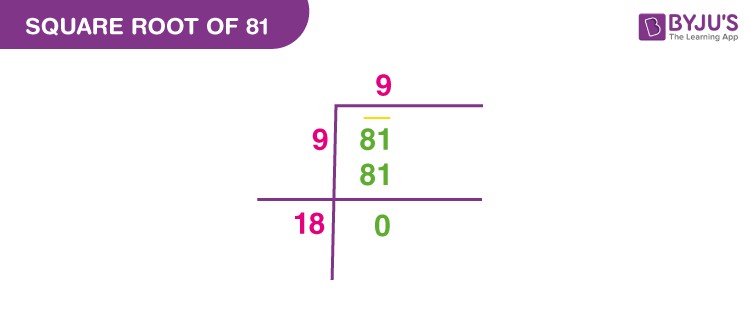
5. Applying the Long Division Method to Find the Square Root of 81
The long division method is a systematic approach to find the square root of a number, especially useful for larger numbers and non-perfect squares. While it might seem complex initially, it’s a reliable technique once mastered.
To find the square root of 81 using the long division method:
-
Write the Number: Write the number 81. Pair the digits from right to left by placing a bar over the number. In this case, it’s simply 81.
-
Find a Number Whose Square is Less Than or Equal to 81: Look for a number that, when multiplied by itself, is less than or equal to 81. In this case, 9 × 9 = 81.
-
Perform the Division:
- Write 9 as the quotient.
- Subtract 81 (9 × 9) from 81, which leaves a remainder of 0.
9 ------ 9 | 81 - 81 ------ 0 -
Result: The quotient is 9, and the remainder is 0.
Therefore, the square root of 81, using the long division method, is 9.
Key points about the long division method:
- Applicable to All Numbers: Can be used for perfect squares, non-perfect squares, and large numbers.
- Systematic Approach: Provides a step-by-step method to accurately find square roots.
- Foundation for Advanced Mathematics: Essential for understanding more complex mathematical operations.
Here’s a summary:
| Step | Description | Result |
|---|---|---|
| 1. Pairing Digits | Pair 81 from right to left | 81 |
| 2. Finding the Divisor | Find a number (9) such that 9 × 9 ≤ 81 | 9 |
| 3. Performing Division | Divide 81 by 9, subtract the product (81) | 0 |
| 4. Result | The square root is the quotient (9) | 9 |
The long division method confirms that √81 = 9. If you need further assistance or have more questions, please visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. Contact us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for additional support.
 Long Division Method Example
Long Division Method Example
6. Practical Examples of Using the Square Root of 81
Understanding the square root of 81 is not just a theoretical exercise; it has numerous practical applications in various fields. Let’s explore some examples where knowing the square root of 81 can be useful.
-
Geometry:
- Area of a Square: If you have a square with an area of 81 square units, the length of each side is the square root of 81, which is 9 units. This is a fundamental concept in geometry for calculating dimensions.
- Example: Suppose you’re designing a square garden with an area of 81 square feet. To determine how much fencing you need, you calculate the side length as √81 = 9 feet. Therefore, each side is 9 feet long.
-
Construction:
- Calculating Dimensions: Builders often use square roots to ensure structures are square and have the correct proportions.
- Example: A construction worker needs to create a square foundation with an area of 81 square meters. They use the square root to determine that each side should be 9 meters long.
-
Physics:
- Kinematics: Square roots are used in kinematic equations to calculate velocity, acceleration, and displacement.
- Example: In a physics problem, if the kinetic energy of an object is related to the square of its velocity and you know a certain value involves the square root of 81, knowing that √81 = 9 helps simplify the calculation.
-
Computer Science:
- Algorithms: Square roots are used in various algorithms, such as those for image processing and data analysis.
- Example: In a program that requires determining the size of a square matrix, knowing that the square root of 81 is 9 can help optimize the algorithm for matrices of that size.
-
Everyday Life:
- Home Improvement: When planning home improvement projects, such as tiling a square area, understanding square roots helps in determining the dimensions.
- Example: You want to tile a square area of your bathroom floor that measures 81 square feet. Knowing that √81 = 9 helps you determine that each side of the square area is 9 feet, making it easier to plan the tiling layout.
These examples illustrate how the square root of 81 is applied across different domains, highlighting its importance in practical problem-solving.
Here’s a summary table:
| Field | Application | Example |
|---|---|---|
| Geometry | Calculating side length of a square | Designing a square garden with an area of 81 sq ft (side length = 9 ft) |
| Construction | Ensuring square foundations have correct dimensions | Creating a square foundation of 81 sq meters (side length = 9 meters) |
| Physics | Kinematic equations | Calculating velocity or acceleration involving √81 |
| Computer Science | Optimizing algorithms for square matrices | Designing algorithms for 9×9 matrices |
| Everyday Life | Home improvement projects | Tiling a square area of 81 sq ft (side length = 9 ft) |
By understanding these applications, you can appreciate the versatility of knowing the square root of 81. For more practical math solutions and explanations, visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can reach us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for additional support.
7. Simplifying Expressions Involving the Square Root of 81
Simplifying expressions involving the square root of 81 is a common task in algebra. Here are some examples of how to simplify such expressions, along with step-by-step solutions.
Example 1: Simplifying √81 + 5
- Problem: Simplify the expression √81 + 5.
- Solution:
- First, find the square root of 81: √81 = 9.
- Substitute the value back into the expression: 9 + 5.
- Add the numbers: 9 + 5 = 14.
- Therefore, √81 + 5 = 14.
Example 2: Simplifying 3√81 – 10
- Problem: Simplify the expression 3√81 – 10.
- Solution:
- Find the square root of 81: √81 = 9.
- Substitute the value back into the expression: 3 × 9 – 10.
- Multiply 3 by 9: 27 – 10.
- Subtract 10 from 27: 27 – 10 = 17.
- Therefore, 3√81 – 10 = 17.
Example 3: Simplifying (√81) / 3 + 7
- Problem: Simplify the expression (√81) / 3 + 7.
- Solution:
- Find the square root of 81: √81 = 9.
- Substitute the value back into the expression: 9 / 3 + 7.
- Divide 9 by 3: 3 + 7.
- Add 3 and 7: 3 + 7 = 10.
- Therefore, (√81) / 3 + 7 = 10.
Example 4: Simplifying 2(√81 + 4) – 5
- Problem: Simplify the expression 2(√81 + 4) – 5.
- Solution:
- Find the square root of 81: √81 = 9.
- Substitute the value back into the expression: 2(9 + 4) – 5.
- Add 9 and 4: 2(13) – 5.
- Multiply 2 by 13: 26 – 5.
- Subtract 5 from 26: 26 – 5 = 21.
- Therefore, 2(√81 + 4) – 5 = 21.
Example 5: Simplifying (√81)^2 + 3
- Problem: Simplify the expression (√81)^2 + 3.
- Solution:
- Find the square root of 81: √81 = 9.
- Substitute the value back into the expression: (9)^2 + 3.
- Square 9: 81 + 3.
- Add 81 and 3: 81 + 3 = 84.
- Therefore, (√81)^2 + 3 = 84.
Here’s a summary table:
| Expression | Simplification Steps | Result |
|---|---|---|
| √81 + 5 | √81 = 9, 9 + 5 | 14 |
| 3√81 – 10 | √81 = 9, 3 × 9 – 10, 27 – 10 | 17 |
| (√81) / 3 + 7 | √81 = 9, 9 / 3 + 7, 3 + 7 | 10 |
| 2(√81 + 4) – 5 | √81 = 9, 2(9 + 4) – 5, 2(13) – 5, 26 – 5 | 21 |
| (√81)^2 + 3 | √81 = 9, (9)^2 + 3, 81 + 3 | 84 |
These examples demonstrate how to simplify various expressions involving the square root of 81. If you have any questions or need further assistance with math problems, please visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also contact us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for additional support.
8. Understanding Perfect Squares and the Square Root of 81
Perfect squares are numbers that are the result of squaring an integer (a whole number). Understanding perfect squares is fundamental to grasping the concept of square roots. The square root of a perfect square is always an integer.
A perfect square is a number that can be obtained by multiplying an integer by itself. For example, 4 is a perfect square because 2 × 2 = 4. Similarly, 9 is a perfect square because 3 × 3 = 9.
Key characteristics of perfect squares:
- Integer Square Roots: The square root of a perfect square is always an integer.
- Non-Negative: Perfect squares are always non-negative (zero or positive).
- Common Examples: Common perfect squares include 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, etc.
Now, let’s consider the number 81. To determine if 81 is a perfect square, we need to find an integer that, when multiplied by itself, equals 81.
Since 9 × 9 = 81, we can conclude that 81 is a perfect square, and its square root is 9.
Here’s a summary table illustrating perfect squares:
| Number | Square (Number × Number) | Perfect Square? |
|---|---|---|
| 1 | 1 × 1 = 1 | Yes |
| 2 | 2 × 2 = 4 | Yes |
| 3 | 3 × 3 = 9 | Yes |
| 4 | 4 × 4 = 16 | Yes |
| 5 | 5 × 5 = 25 | Yes |
| 6 | 6 × 6 = 36 | Yes |
| 7 | 7 × 7 = 49 | Yes |
| 8 | 8 × 8 = 64 | Yes |
| 9 | 9 × 9 = 81 | Yes |
| 10 | 10 × 10 = 100 | Yes |
Understanding perfect squares is essential for various mathematical concepts, including simplifying radicals, solving quadratic equations, and understanding number theory. If you have any questions or need further assistance, please visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also contact us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for additional support.
9. Real-World Applications of Square Roots Beyond Basic Math
Square roots are not just abstract mathematical concepts; they have significant real-world applications beyond basic arithmetic. Understanding these applications can highlight the importance of mastering square roots.
-
Engineering:
- Structural Design: Engineers use square roots to calculate the stability and load-bearing capacity of structures such as bridges and buildings.
- Example: When designing a bridge, engineers need to calculate the tension in cables, which often involves square roots to determine the correct dimensions and materials needed for safety.
-
Physics:
- Calculating Speed and Velocity: Square roots are used in kinematic equations to determine the speed and velocity of objects.
- Example: The velocity (v) of an object in free fall can be calculated using the equation v = √(2gh), where g is the acceleration due to gravity and h is the height.
-
Computer Graphics:
- Distance Calculations: Square roots are used to calculate distances between points in 2D and 3D spaces, which is essential in computer graphics for rendering and animation.
- Example: In video games, the distance between two characters is calculated using the distance formula, which involves square roots, to determine if they can interact or collide.
-
Finance:
- Calculating Investment Returns: Square roots are used in financial calculations to determine annual returns and compound interest rates.
- Example: The Sharpe Ratio, a measure of risk-adjusted return, involves square roots to calculate the standard deviation of investment returns.
-
Navigation:
- GPS Technology: Square roots are used in GPS technology to calculate distances and positions accurately.
- Example: GPS devices use trilateration, which involves calculating distances from multiple satellites to determine a location. These calculations rely heavily on square roots.
-
Medical Imaging:
- Image Reconstruction: Square roots are used in medical imaging techniques like MRI and CT scans to reconstruct images from raw data.
- Example: In MRI, the reconstruction of images from the signals involves complex mathematical transformations that use square roots to enhance image quality.
-
Acoustics:
- Sound Intensity Calculations: Square roots are used to calculate sound intensity and pressure levels.
- Example: The root mean square (RMS) value of sound pressure, which is used to measure sound intensity, involves taking the square root of the average of the squares of the pressure values.
Here’s a summary table highlighting real-world applications of square roots:
| Field | Application | Example |
|---|---|---|
| Engineering | Structural Design | Calculating tension in bridge cables using square roots to ensure stability. |
| Physics | Calculating Speed and Velocity | Determining the velocity of an object in free fall using v = √(2gh). |
| Computer Graphics | Distance Calculations | Calculating the distance between characters in a video game to determine interactions. |
| Finance | Calculating Investment Returns | Using the Sharpe Ratio, which involves square roots, to measure risk-adjusted investment returns. |
| Navigation | GPS Technology | Calculating distances from GPS satellites to determine location using trilateration. |
| Medical Imaging | Image Reconstruction | Reconstructing images from MRI signals using square roots to enhance image quality. |
| Acoustics | Sound Intensity Calculations | Measuring sound intensity using the root mean square (RMS) value of sound pressure. |
These real-world examples demonstrate that square roots are essential tools in various fields, making their understanding crucial for problem-solving and innovation. If you have any questions or need further assistance, please visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also contact us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for additional support.
10. Frequently Asked Questions (FAQs) About the Square Root of 81
To further clarify the concept of the square root of 81, here are some frequently asked questions along with their answers.
| Question | Answer |
|---|---|
| What is the value of the square root of 81? | The square root of 81 is 9, because 9 multiplied by itself (9 × 9) equals 81. |
| Is the square root of 81 a rational number? | Yes, the square root of 81 is a rational number. A rational number can be expressed as a fraction p/q, where p and q are integers and q is not zero. In this case, 9 can be written as 9/1. |
| Is 81 a perfect square? | Yes, 81 is a perfect square because its square root, 9, is an integer. A perfect square is a number that can be obtained by squaring an integer. |
| What is the negative square root of 81? | The negative square root of 81 is -9, because -9 multiplied by itself (-9 × -9) also equals 81. |
| How do you find the square root of 81? | There are several methods to find the square root of 81, including prime factorization, repeated subtraction, and long division. Each method provides a different approach to arriving at the same answer. |
| Can the square root of 81 be a decimal? | No, the principal square root of 81 is not a decimal. It is an integer, 9. However, some numbers have square roots that are decimals (e.g., the square root of 2). |
| What is the radical form of the square root of 81? | The radical form of the square root of 81 is √81. This is the notation used to represent the square root of 81 before it is simplified to 9. |
| Is the square root of 81 an irrational number? | No, the square root of 81 is not an irrational number. Irrational numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal representations. |
| What is the square of the square root of 81? | The square of the square root of 81 is 81. This is because squaring a square root cancels out the root operation, returning the original number. (√81)^2 = 81. |
| Where can I ask more questions about square roots? | You can ask more questions about square roots and other math topics at WHAT.EDU.VN. We provide a platform for free answers and assistance with your educational needs. |
For any further questions or assistance, please visit WHAT.EDU.VN. We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can also contact us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN for additional support.
Are you still curious about the square root of 81 or have any other questions? Don’t hesitate to ask at WHAT.EDU.VN, where you can get free answers to all your questions. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States or via Whatsapp at +1 (206) 555-7890. Visit what.edu.vn today and get the answers you need!