What Is Volume In Math? A Comprehensive Guide

What Is Volume In Math? It’s the measure of the 3D space an object occupies, crucial for everything from filling containers to understanding geometry. At WHAT.EDU.VN, we provide clear, concise answers to your math questions, making complex concepts accessible to everyone. Explore volume calculation, real-world applications, and formulas with us.

1. Understanding the Basics of Volume in Math

Volume in mathematics refers to the amount of three-dimensional space enclosed within a boundary. Think of it as the capacity of an object—how much water a bottle can hold, or how much air fills a room. This measurement is essential in various fields, from construction and engineering to everyday tasks like cooking and packing. It quantifies the size of an object in three dimensions, providing a comprehensive understanding of its spatial extent. Understanding volume is fundamental to grasping spatial relationships and solving practical problems.

Volume is a scalar quantity, meaning it has magnitude but no direction. It is typically measured in cubic units, such as cubic meters (m³), cubic centimeters (cm³), cubic feet (ft³), or cubic inches (in³). The choice of unit depends on the size of the object being measured; smaller objects might be measured in cubic centimeters, while larger spaces like rooms or buildings are measured in cubic meters or cubic feet.

The concept of volume is closely related to other geometric measurements like length, area, and perimeter. While length measures one-dimensional space, area measures two-dimensional space, and volume measures three-dimensional space. Understanding these distinctions is crucial for accurately describing and analyzing the properties of objects in our physical world. For instance, knowing the area of a floor helps determine how much flooring material is needed, while knowing the volume of a container helps determine how much it can hold.

Three-dimensional Space: The space an object occupies in terms of length, width, and height.
Cubic Units: Units such as cm³, m³, ft³, or in³ used to measure volume.
Scalar Quantity: A quantity with magnitude but no direction.

2. The Significance of Volume in Real-World Applications

Volume isn’t just a theoretical concept—it has countless practical applications in our daily lives. In cooking, volume is essential for measuring ingredients accurately to ensure recipes turn out as expected. In construction, it’s used to calculate the amount of concrete needed for a foundation or the amount of insulation required for a room. In medicine, volume is used to measure dosages of liquid medications and to monitor fluid levels in the body. Understanding volume allows for precise measurements and calculations, leading to better outcomes in various fields.

In environmental science, volume is crucial for assessing water resources in lakes, rivers, and reservoirs. By calculating the volume of water bodies, scientists can monitor water availability, manage water supplies, and assess the impact of climate change on water resources. Similarly, in transportation, volume is used to determine the capacity of cargo containers, trucks, and ships, ensuring efficient and safe transportation of goods. The accurate measurement of volume is vital for logistics, supply chain management, and international trade.

Volume also plays a significant role in product design and packaging. Manufacturers need to determine the volume of their products to design appropriate packaging materials and sizes. This ensures that products are protected during transportation and storage, while also minimizing waste and reducing costs. In chemistry and physics, volume is used to measure the amount of substances in experiments and industrial processes, ensuring accurate results and efficient use of resources.

Cooking: Measuring ingredients for recipes.
Construction: Calculating materials like concrete and insulation.
Medicine: Measuring liquid dosages and monitoring fluid levels.

3. Key Formulas for Calculating Volume

Calculating volume involves using specific formulas depending on the shape of the object. Here are some of the most common shapes and their corresponding volume formulas:

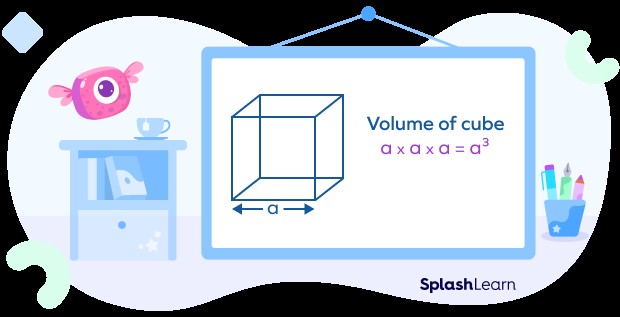
Cube: A cube has equal sides, so the volume is calculated by multiplying the length of one side by itself three times: V = a³, where ‘a’ is the length of a side.
Cuboid (Rectangular Prism): A cuboid has different lengths for its sides. The volume is calculated by multiplying the length, width, and height: V = l × w × h.
Sphere: The volume of a sphere is calculated using the formula: V = (4/3) × π × r³, where ‘r’ is the radius of the sphere and π (pi) is approximately 3.14159.
Cylinder: A cylinder has circular bases and a height. The volume is calculated by multiplying the area of the base (πr²) by the height: V = π × r² × h, where ‘r’ is the radius of the base and ‘h’ is the height.
Cone: The volume of a cone is one-third of the volume of a cylinder with the same base and height: V = (1/3) × π × r² × h, where ‘r’ is the radius of the base and ‘h’ is the height.
Pyramid: The volume of a pyramid is calculated as one-third of the base area times the height: V = (1/3) × B × h, where ‘B’ is the area of the base and ‘h’ is the height.

These formulas are essential tools for calculating the volume of various objects in different contexts. Understanding when and how to apply each formula is crucial for accurate measurements and problem-solving. Whether you’re calculating the volume of a storage container or designing a new product, these formulas provide a reliable method for determining the spatial extent of three-dimensional objects.

Cube: V = a³
Cuboid: V = l × w × h
Sphere: V = (4/3) × π × r³
Cylinder: V = π × r² × h
Cone: V = (1/3) × π × r² × h
Pyramid: V = (1/3) × B × h

4. Step-by-Step Guide to Calculating Volume for Different Shapes

Calculating volume can seem daunting, but breaking it down into simple steps makes it manageable. Here’s a step-by-step guide for calculating the volume of different shapes:

Identify the Shape: Determine the type of three-dimensional shape you’re dealing with (e.g., cube, cuboid, sphere, cylinder, cone, pyramid).
Gather Measurements: Obtain the necessary measurements for the shape. This might include the length of a side (for a cube), length, width, and height (for a cuboid), radius (for a sphere or cylinder), or base area and height (for a pyramid).
Choose the Correct Formula: Select the appropriate volume formula for the shape you’re working with. Refer to the formulas provided in the previous section.
Plug in the Values: Substitute the measurements you gathered into the volume formula. Make sure all measurements are in the same units (e.g., all in centimeters or all in meters).
Perform the Calculation: Perform the mathematical operations in the formula to calculate the volume. Use a calculator if necessary to ensure accuracy.
Include the Units: Write the volume with the appropriate cubic units (e.g., cm³, m³, ft³).

For example, let’s calculate the volume of a cylinder with a radius of 5 cm and a height of 10 cm:

Shape: Cylinder
Measurements: Radius (r) = 5 cm, Height (h) = 10 cm
Formula: V = π × r² × h
Plug in Values: V = π × (5 cm)² × 10 cm
Calculation: V = π × 25 cm² × 10 cm = 250π cm³ ≈ 785.4 cm³
Units: The volume of the cylinder is approximately 785.4 cm³.

By following these steps, you can confidently calculate the volume of various shapes and apply this knowledge to practical problems.

Step 1: Identify the shape.
Step 2: Gather measurements.
Step 3: Choose the correct formula.
Step 4: Plug in the values.
Step 5: Perform the calculation.
Step 6: Include the units.

5. Tips and Tricks for Accurate Volume Calculation

Accurate volume calculation requires careful attention to detail and a systematic approach. Here are some tips and tricks to help you avoid common mistakes and ensure precise measurements:

Use the Same Units: Always ensure that all measurements are in the same units before performing any calculations. If necessary, convert measurements to a common unit (e.g., convert all measurements to centimeters or meters).
Double-Check Measurements: Verify the accuracy of your measurements before plugging them into the formula. Small errors in measurement can lead to significant errors in the final volume calculation.
Use a Calculator: Use a calculator for complex calculations to minimize the risk of mathematical errors. This is particularly important when dealing with formulas involving π or exponents.
Understand the Formula: Make sure you understand the correct formula for the shape you’re working with. Using the wrong formula will result in an incorrect volume calculation.
Break Down Complex Shapes: If you’re dealing with a complex shape, break it down into simpler shapes for which you can easily calculate the volume. Then, add the individual volumes to find the total volume.
Estimate the Volume: Before performing the calculation, estimate the volume to get a sense of the expected result. This can help you identify potential errors in your calculations.
Practice Regularly: Practice calculating the volume of different shapes regularly to improve your skills and build confidence. The more you practice, the more comfortable you’ll become with the process.
Use Online Tools: Take advantage of online volume calculators and resources to check your work and gain a better understanding of the concepts. These tools can provide instant feedback and help you identify areas where you need to improve.

By following these tips and tricks, you can improve your accuracy and efficiency in volume calculation and confidently tackle a wide range of practical problems.

Ensure Same Units: Convert all measurements to a common unit.
Double-Check: Verify the accuracy of measurements.
Use a Calculator: Minimize mathematical errors.
Understand the Formula: Use the correct formula for the shape.
Break Down Shapes: Simplify complex shapes into basic shapes.
Estimate Volume: Check for potential errors.
Practice Regularly: Improve skills through practice.
Use Online Tools: Check your work with online calculators.

6. Common Mistakes to Avoid When Calculating Volume

Calculating volume can be tricky, and it’s easy to make mistakes if you’re not careful. Here are some common errors to watch out for:

Using the Wrong Formula: One of the most common mistakes is using the wrong formula for the shape you’re working with. Double-check the shape and make sure you’re using the appropriate formula.
Incorrect Units: Failing to use consistent units is another frequent mistake. Ensure that all measurements are in the same units before performing calculations.
Math Errors: Simple arithmetic errors can lead to incorrect volume calculations. Use a calculator to avoid mistakes, especially when dealing with complex formulas.
Measuring Incorrectly: Inaccurate measurements can significantly affect the final volume calculation. Take your time and measure carefully, using the correct tools for the job.
Forgetting to Include Units: Always include the appropriate cubic units (e.g., cm³, m³, ft³) when stating the volume.
Not Understanding the Shape: A lack of understanding of the shape can lead to using the wrong measurements in the formula. Familiarize yourself with the properties of each shape.
Skipping Steps: Rushing through the calculation process can lead to errors. Follow the steps carefully and double-check your work at each stage.
Ignoring Significant Figures: When dealing with decimal numbers, pay attention to significant figures to ensure your answer is accurate and meaningful.

By being aware of these common mistakes and taking steps to avoid them, you can improve the accuracy of your volume calculations and confidently solve a wide range of practical problems.

Wrong Formula: Double-check the formula for the shape.
Incorrect Units: Ensure consistent units for all measurements.
Math Errors: Use a calculator for complex calculations.
Measuring Incorrectly: Measure carefully and use the correct tools.
Forgetting Units: Always include the cubic units.
Not Understanding Shape: Familiarize yourself with shape properties.
Skipping Steps: Follow each step carefully.
Ignoring Significant Figures: Pay attention to decimal numbers.

7. Advanced Volume Calculations: Irregular Shapes and Composite Objects

While basic volume calculations focus on regular shapes like cubes, spheres, and cylinders, many real-world objects have irregular shapes or are composite objects made up of multiple shapes. Calculating the volume of these objects requires more advanced techniques. Here are some strategies:

Displacement Method: The displacement method involves immersing an irregular object in a liquid (usually water) and measuring the volume of liquid displaced. This method is based on Archimedes’ principle, which states that the volume of the displaced liquid is equal to the volume of the object.
Decomposition into Simpler Shapes: Complex objects can be broken down into simpler shapes, such as cubes, cuboids, cylinders, and cones. Calculate the volume of each simpler shape and then add them together to find the total volume.
Integration: In calculus, integration can be used to find the volume of objects with curved surfaces or irregular shapes. This method involves setting up an integral that represents the volume and then evaluating the integral.
3D Scanning: 3D scanning technology can be used to create a digital model of an irregular object. The volume of the object can then be calculated using specialized software.
Approximation Techniques: For some irregular objects, it may be necessary to use approximation techniques, such as dividing the object into small, regular shapes and summing their volumes.

These advanced techniques require a deeper understanding of mathematics and may involve the use of specialized tools and software. However, they provide a powerful way to calculate the volume of complex objects that cannot be easily measured using basic formulas.

Displacement Method: Measure displaced liquid volume.
Decomposition: Break into simpler shapes.
Integration: Use calculus for curved surfaces.
3D Scanning: Create digital models for volume calculation.
Approximation: Divide into small, regular shapes.

8. Volume in Different Measurement Systems: Metric vs. Imperial

Volume is measured using different units in the metric and imperial measurement systems. Understanding these differences is essential for accurate conversions and calculations.

Metric System

In the metric system, the basic unit of volume is the cubic meter (m³). However, smaller units like cubic centimeters (cm³) and liters (L) are commonly used for everyday measurements.

Cubic Meter (m³): The volume of a cube with sides of 1 meter each.
Cubic Centimeter (cm³): The volume of a cube with sides of 1 centimeter each. 1 cm³ = 1 mL (milliliter).
Liter (L): A unit of volume equal to 1000 cubic centimeters. 1 L = 1000 cm³.
Milliliter (mL): A unit of volume equal to 1 cubic centimeter. 1 mL = 1 cm³.

Imperial System

In the imperial system, volume is measured in units like cubic inches (in³), cubic feet (ft³), cubic yards (yd³), fluid ounces (fl oz), pints (pt), quarts (qt), and gallons (gal).

Cubic Inch (in³): The volume of a cube with sides of 1 inch each.
Cubic Foot (ft³): The volume of a cube with sides of 1 foot each. 1 ft³ = 1728 in³.
Cubic Yard (yd³): The volume of a cube with sides of 1 yard each. 1 yd³ = 27 ft³.
Fluid Ounce (fl oz): A unit of volume commonly used for liquids.
Pint (pt): A unit of volume equal to 16 fluid ounces.
Quart (qt): A unit of volume equal to 2 pints or 32 fluid ounces.
Gallon (gal): A unit of volume equal to 4 quarts, 8 pints, or 128 fluid ounces.

Conversion Between Systems

Converting between metric and imperial units requires using conversion factors. Here are some common conversions:

1 inch = 2.54 centimeters
1 foot = 0.3048 meters
1 yard = 0.9144 meters
1 cubic inch = 16.387 cubic centimeters
1 cubic foot = 0.0283 cubic meters
1 fluid ounce = 29.574 milliliters
1 liter = 0.264 gallons

Understanding these units and conversions is crucial for accurate measurements and calculations, especially in fields that require working with both metric and imperial systems.

Metric System: m³, cm³, L, mL
Imperial System: in³, ft³, yd³, fl oz, pt, qt, gal
Conversions: Know the conversion factors between systems.

9. Practical Examples and Exercises for Mastering Volume

To truly master the concept of volume, it’s essential to practice with real-world examples and exercises. Here are some practical examples and exercises to help you solidify your understanding:

Examples

Aquarium Volume: Calculate the volume of an aquarium that is 80 cm long, 40 cm wide, and 50 cm high.
- Volume = length × width × height = 80 cm × 40 cm × 50 cm = 160,000 cm³ = 160 liters.
Spherical Balloon: Find the volume of a spherical balloon with a radius of 15 cm.
- Volume = (4/3) × π × r³ = (4/3) × π × (15 cm)³ ≈ 14,137 cm³.
Cylindrical Can: Determine the volume of a cylindrical can with a radius of 6 cm and a height of 12 cm.
- Volume = π × r² × h = π × (6 cm)² × 12 cm ≈ 1,357 cm³.
Conical Pile of Sand: Calculate the volume of a conical pile of sand with a base radius of 1 meter and a height of 1.5 meters.
- Volume = (1/3) × π × r² × h = (1/3) × π × (1 m)² × 1.5 m ≈ 1.57 m³.

Exercises

Box Volume: A rectangular box has a length of 25 cm, a width of 15 cm, and a height of 10 cm. What is its volume?
Beach Ball Volume: A beach ball has a radius of 20 cm. Calculate its volume.
Water Tank Volume: A cylindrical water tank has a radius of 3 meters and a height of 5 meters. What is its volume?
Ice Cream Cone Volume: An ice cream cone has a radius of 3 cm and a height of 8 cm. Find its volume.
Pyramid Volume: A pyramid has a square base with sides of 4 meters and a height of 6 meters. Calculate its volume.
Swimming Pool Volume: A swimming pool is 10 meters long, 5 meters wide, and 2 meters deep. What is its volume?

These examples and exercises provide practical applications of volume calculations and can help you develop a deeper understanding of the concept.

Aquarium: Practice cuboid volume calculation.
Balloon: Calculate sphere volume.
Cylindrical Can: Apply cylinder volume formula.
Conical Pile: Practice cone volume calculation.
Exercises: Solve various volume problems.

10. The Future of Volume Measurement: Innovations and Technologies

The field of volume measurement is constantly evolving, with new innovations and technologies emerging to improve accuracy, efficiency, and convenience. Here are some exciting developments shaping the future of volume measurement:

3D Scanning and Modeling: 3D scanning technology allows for the creation of highly accurate digital models of objects. These models can then be used to calculate the volume of even the most complex and irregular shapes.
Laser Measurement: Laser-based measurement systems provide precise and non-contact volume measurements. These systems are used in a variety of applications, including industrial automation, quality control, and scientific research.
Virtual Reality (VR) and Augmented Reality (AR): VR and AR technologies are being used to create immersive environments for visualizing and interacting with three-dimensional objects. These technologies can enhance understanding of volume and spatial relationships.
Artificial Intelligence (AI) and Machine Learning (ML): AI and ML algorithms are being developed to automate volume calculations and improve the accuracy of measurements. These algorithms can analyze data from various sources, such as sensors and images, to estimate volume in real-time.
Smart Sensors: Smart sensors are being integrated into everyday objects and devices to measure volume automatically. For example, smart containers can measure the volume of their contents, providing real-time inventory management.
Cloud-Based Platforms: Cloud-based platforms are enabling remote access to volume measurement data and tools. This allows for collaboration and data sharing among users, as well as centralized data storage and analysis.
Nanotechnology: Nanotechnology is being used to develop new materials and devices for measuring volume at the nanoscale. This is enabling advancements in fields such as medicine, materials science, and environmental monitoring.

These innovations and technologies are transforming the way we measure and understand volume, opening up new possibilities for scientific discovery, engineering design, and industrial automation.

3D Scanning: Accurate digital models for volume calculation.
Laser Measurement: Precise and non-contact measurements.
VR/AR: Immersive environments for visualizing volume.
AI/ML: Automating volume calculations.
Smart Sensors: Automatic volume measurement in objects.
Cloud Platforms: Remote access to data and tools.
Nanotechnology: Volume measurement at the nanoscale.

Understanding what is volume in math opens doors to a world of practical applications and advanced technologies. Whether you’re a student, engineer, or simply curious, mastering volume calculation is a valuable skill.

Do you have more questions about volume or any other math concepts? Don’t struggle alone! At WHAT.EDU.VN, we offer a free platform where you can ask any question and receive quick, accurate answers from experts. We understand the challenges of finding reliable information, and that’s why we’re dedicated to providing a user-friendly service that connects you with knowledgeable individuals who can help you succeed.

Visit us today at WHAT.EDU.VN and experience the convenience of free, expert advice. Our platform is designed to make learning easy and accessible for everyone.

Address: 888 Question City Plaza, Seattle, WA 98101, United States

WhatsApp: +1 (206) 555-7890

Website: WHAT.EDU.VN

Don’t hesitate—your questions deserve answers, and we’re here to provide them. Join the what.edu.vn community and unlock a world of knowledge at your fingertips.