Prime Number Is What exactly? If you’re pondering this fundamental question, you’ve come to the right place. At WHAT.EDU.VN, we provide clear and comprehensive explanations of mathematical concepts, making learning accessible for everyone. Discover the definition, properties, and real-world applications of prime numbers, and unlock the secrets of these fascinating building blocks of mathematics. With our user-friendly platform, complex topics become easy to grasp, supported by expert insights and practical examples. Explore the nuances of prime numbers, including their role in encryption and computer science, with related keywords such as composite numbers, factors, and divisibility.
1. What Are Prime Numbers?
A prime number is a whole number greater than 1 that has only two distinct positive divisors: 1 and itself. In other words, a prime number cannot be evenly divided by any other number except 1 and itself. This unique characteristic sets them apart from other numbers and makes them fundamental in number theory.
Understanding the Prime Number Definition
The definition of a prime number is concise yet powerful. It emphasizes two critical criteria:
- Greater than 1: The number must be larger than one. The number 1 is not considered a prime number because it only has one divisor (itself).
- Exactly two distinct divisors: The number must be divisible only by 1 and itself. If it’s divisible by any other positive integer, it is not prime.
Prime Numbers Examples
To illustrate, let’s consider a few examples:
- 2: The number 2 is prime because it is only divisible by 1 and 2. It is also the smallest and only even prime number.
- 3: The number 3 is prime because it is only divisible by 1 and 3.
- 5: The number 5 is prime because it is only divisible by 1 and 5.
- 7: The number 7 is prime because it is only divisible by 1 and 7.
- 11: The number 11 is prime because it is only divisible by 1 and 11.
In contrast, consider the number 4. It is divisible by 1, 2, and 4. Since it has more than two divisors, it is not a prime number. Numbers with more than two divisors are called composite numbers.
2. Why Are Prime Numbers Important?
Prime numbers are not just abstract mathematical concepts; they have significant applications in various fields, making them indispensable in modern technology and cryptography.
Cryptography and Encryption
One of the most critical applications of prime numbers is in cryptography, the art of secure communication. Many encryption algorithms, such as RSA (Rivest–Shamir–Adleman), rely on the fact that it is computationally difficult to factor large numbers into their prime factors.
RSA Encryption
RSA encryption works by selecting two large prime numbers, p and q, and multiplying them to get a composite number, n. The security of the RSA algorithm depends on the difficulty of factoring n back into p and q. The larger the prime numbers used, the more secure the encryption.
Importance in Cybersecurity
In cybersecurity, prime numbers are fundamental in protecting sensitive information, securing online transactions, and ensuring the privacy of communications. Without prime numbers, much of the digital security we rely on today would be impossible.
Computer Science
Prime numbers also play a vital role in computer science, particularly in hashing algorithms and data structures.
Hashing Algorithms
Hashing algorithms use prime numbers to distribute data evenly across hash tables, reducing the likelihood of collisions. A collision occurs when two different pieces of data are assigned the same hash value, which can slow down data retrieval. Using prime numbers in hashing functions helps minimize these collisions.
Data Structures
In data structures like skip lists and Bloom filters, prime numbers are used to optimize performance and efficiency. These applications leverage the unique properties of prime numbers to improve the speed and reliability of data storage and retrieval.
Mathematical Foundations
Beyond practical applications, prime numbers are essential in various mathematical theorems and proofs. They form the foundation for many advanced mathematical concepts and are crucial in understanding the structure of numbers.
Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, up to the order of the factors. This theorem highlights the fundamental role of prime numbers as the building blocks of all integers.
Number Theory
In number theory, prime numbers are studied extensively, leading to many fascinating discoveries and unsolved problems. Some famous conjectures, like the Riemann Hypothesis, are related to the distribution of prime numbers and remain open challenges for mathematicians.
3. How to Identify Prime Numbers
Identifying whether a number is prime involves testing its divisibility. Here are a few methods to determine if a number is prime:
Trial Division
The most straightforward method is trial division. To check if a number n is prime, divide it by all integers from 2 to the square root of n. If none of these integers divide n evenly, then n is prime.
Algorithm for Trial Division
- Start with the number n that you want to test for primality.
- For each integer i from 2 to the square root of n:
- If n is divisible by i (i.e., n % i == 0), then n is not prime.
- If no divisor is found, then n is prime.
Example of Trial Division
Let’s test if 31 is a prime number:
- The square root of 31 is approximately 5.57.
- We need to check divisibility by integers from 2 to 5.
- 31 % 2 = 1 (not divisible)
- 31 % 3 = 1 (not divisible)
- 31 % 4 = 3 (not divisible)
- 31 % 5 = 1 (not divisible)
- Since 31 is not divisible by any integer from 2 to 5, it is a prime number.
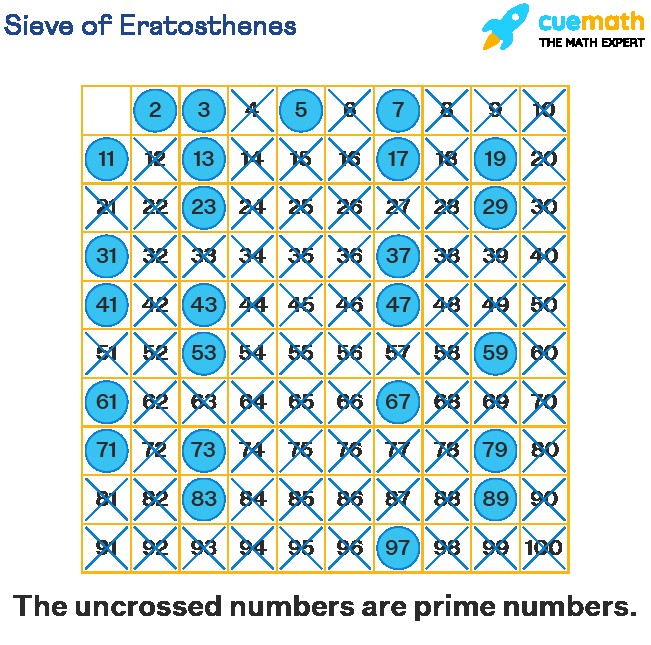
Sieve of Eratosthenes
The Sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to a specified integer. It works by iteratively marking the multiples of each prime, starting with the first prime number, 2.
Algorithm for Sieve of Eratosthenes
- Create a list of consecutive integers from 2 to n.
- Start with the first prime number, p = 2.
- Mark all multiples of p greater than p itself (2p, 3p, 4p, …) as composite.
- Find the next number in the list that has not been marked as composite. If there is no such number, stop. Otherwise, let this number be the new p (the next prime number).
- Repeat steps 3 and 4.
Example of Sieve of Eratosthenes
To find all prime numbers up to 30 using the Sieve of Eratosthenes:
- Create a list of integers from 2 to 30.
- Start with p = 2.
- Mark all multiples of 2 (4, 6, 8, …, 30) as composite.
- The next unmarked number is 3. Mark all multiples of 3 (6, 9, 12, …, 30) as composite.
- The next unmarked number is 5. Mark all multiples of 5 (10, 15, 20, 25, 30) as composite.
- Continue this process until all multiples of prime numbers up to the square root of 30 have been marked.
- The remaining unmarked numbers (2, 3, 5, 7, 11, 13, 17, 19, 23, 29) are the prime numbers up to 30.
Primality Tests
For very large numbers, more sophisticated primality tests are used, such as the Miller-Rabin primality test and the AKS primality test. These tests are probabilistic and deterministic, respectively, and are designed to efficiently determine whether a large number is prime.
Miller-Rabin Primality Test
The Miller-Rabin test is a probabilistic algorithm that determines whether a given number is prime. It is based on properties of strong pseudoprimes and is widely used in practice due to its speed and relatively high accuracy.
AKS Primality Test
The AKS primality test is the first deterministic, polynomial-time primality test. It guarantees whether a number is prime or composite without relying on unproven conjectures. While it is theoretically significant, it is less practical for very large numbers compared to probabilistic tests.
4. Types of Prime Numbers
Prime numbers come in various forms, each with unique characteristics and applications.
Mersenne Primes
Mersenne primes are prime numbers that are one less than a power of two. They are of the form 2^n – 1, where n is a prime number. Mersenne primes are named after Marin Mersenne, a French monk who studied them in the 17th century.
Examples of Mersenne Primes
- 3 = 2^2 – 1
- 7 = 2^3 – 1
- 31 = 2^5 – 1
- 127 = 2^7 – 1
Mersenne primes are particularly interesting because they can be efficiently tested for primality using the Lucas-Lehmer primality test. As a result, the largest known prime numbers are often Mersenne primes.
Fermat Primes
Fermat primes are prime numbers of the form 2^(2^n) + 1, where n is a non-negative integer. They are named after Pierre de Fermat, a 17th-century mathematician who conjectured that all numbers of this form were prime.
Examples of Fermat Primes
- 3 = 2^(2^0) + 1
- 5 = 2^(2^1) + 1
- 17 = 2^(2^2) + 1
- 257 = 2^(2^3) + 1
- 65537 = 2^(2^4) + 1
Only the first five Fermat numbers (for n = 0, 1, 2, 3, and 4) are known to be prime. It is an open question whether any other Fermat numbers are prime.
Twin Primes
Twin primes are pairs of prime numbers that differ by 2. For example, (3, 5), (5, 7), and (11, 13) are twin primes.
Twin Prime Conjecture
The Twin Prime Conjecture states that there are infinitely many twin primes. This conjecture remains unproven, but it is one of the most famous unsolved problems in number theory.
Other Types
- Sophie Germain Primes: A prime p is a Sophie Germain prime if 2p + 1 is also prime.
- Safe Primes: A prime q is a safe prime if (q-1)/2 is also prime. Safe primes are often used in cryptography because they provide additional security.
5. List of Prime Numbers
Here is a list of prime numbers, which can be useful for quick reference and educational purposes.
Prime Numbers From 1 to 100
The prime numbers from 1 to 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
Prime Numbers From 101 to 200
The prime numbers from 101 to 200 are:
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
This list can be extended indefinitely, as there are infinitely many prime numbers.
6. Real-World Applications of Prime Numbers
The abstract nature of prime numbers might lead one to believe they are confined to theoretical mathematics. However, prime numbers have numerous practical applications that impact our daily lives.
Internet Security
As mentioned earlier, prime numbers are a cornerstone of internet security. Encryption algorithms like RSA use large prime numbers to secure online transactions, protect sensitive data, and ensure secure communication. Without prime numbers, e-commerce, online banking, and secure email would be vulnerable to eavesdropping and fraud.
Securing Data Transmission
When you make an online purchase, your credit card information is encrypted using prime numbers to prevent unauthorized access. The difficulty of factoring large composite numbers into their prime factors ensures that only the intended recipient can decrypt the message.
Error Correction
Prime numbers are used in error correction codes, which are essential for ensuring the reliability of data storage and transmission. These codes detect and correct errors that may occur due to noise or interference.
Data Storage
In data storage devices like hard drives and solid-state drives, error correction codes based on prime numbers help maintain data integrity. These codes ensure that data is accurately stored and retrieved, even in the presence of physical defects or electrical disturbances.
Random Number Generation
Prime numbers are used in generating pseudo-random numbers, which are essential for simulations, statistical analysis, and computer games. These algorithms use mathematical formulas based on prime numbers to produce sequences of numbers that appear random.
Simulations
In scientific simulations, pseudo-random numbers are used to model complex systems and processes. Prime numbers help ensure that these simulations are accurate and reliable.
Musical Harmony
Interestingly, prime numbers have been found to have connections to musical harmony. Some theories suggest that the ratios of prime numbers correspond to harmonious musical intervals.
Music Composition
Composers have used prime numbers to create musical structures and patterns. These patterns can add complexity and interest to musical compositions.
7. Prime Numbers vs. Composite Numbers
Understanding the difference between prime numbers and composite numbers is crucial for mastering number theory.
Definition of Composite Numbers
A composite number is a positive integer that has more than two distinct positive divisors. In other words, a composite number can be divided evenly by at least one number other than 1 and itself.
Examples of Composite Numbers
- 4 is a composite number because it is divisible by 1, 2, and 4.
- 6 is a composite number because it is divisible by 1, 2, 3, and 6.
- 8 is a composite number because it is divisible by 1, 2, 4, and 8.
- 9 is a composite number because it is divisible by 1, 3, and 9.
- 10 is a composite number because it is divisible by 1, 2, 5, and 10.
Key Differences
The key difference between prime and composite numbers is the number of divisors:
- Prime Numbers: Exactly two distinct positive divisors (1 and itself).
- Composite Numbers: More than two distinct positive divisors.
Relationship
Every positive integer greater than 1 is either prime or composite. The number 1 is neither prime nor composite, as it has only one divisor.
8. Common Misconceptions About Prime Numbers
There are several common misconceptions about prime numbers that can lead to confusion. Let’s address some of these misconceptions.
Misconception 1: All Odd Numbers Are Prime
It is a common mistake to assume that all odd numbers are prime. While many prime numbers are odd, this is not always the case. For example, the number 9 is odd but is divisible by 1, 3, and 9, making it a composite number.
Misconception 2: Prime Numbers Follow a Pattern
Another misconception is that prime numbers follow a predictable pattern. In reality, the distribution of prime numbers is irregular and unpredictable. Mathematicians have studied prime numbers for centuries, but there is still no known formula to generate all prime numbers.
Misconception 3: 1 Is a Prime Number
It is essential to remember that 1 is not a prime number. According to the definition, a prime number must have exactly two distinct positive divisors. The number 1 has only one divisor (itself), so it does not meet the criteria for being a prime number.
Misconception 4: Prime Numbers Are Useless
As we have discussed, prime numbers have numerous practical applications in cryptography, computer science, and other fields. They are not just abstract mathematical concepts but essential tools for securing data, optimizing algorithms, and ensuring the reliability of systems.
9. How to Factor a Number Into Primes
Factoring a number into its prime factors involves breaking down the number into a product of prime numbers. This process is also known as prime factorization.
Method
- Start with the number you want to factor.
- Divide the number by the smallest prime number, 2, if possible.
- If the number is divisible by 2, repeat the process until it is no longer divisible by 2.
- Move to the next prime number, 3, and repeat the process.
- Continue this process with the next prime numbers (5, 7, 11, …) until the remaining factor is a prime number.
Example
Let’s factor the number 84 into its prime factors:
- 84 is divisible by 2: 84 = 2 * 42
- 42 is divisible by 2: 42 = 2 * 21
- 21 is not divisible by 2, so we move to the next prime number, 3.
- 21 is divisible by 3: 21 = 3 * 7
- 7 is a prime number, so we stop.
The prime factorization of 84 is 2 2 3 7, or 2^2 3 * 7.
Importance
Prime factorization is essential in many areas of mathematics, including number theory, cryptography, and computer science. It is also used in simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM).
10. Interesting Facts About Prime Numbers
Prime numbers are full of surprises and have fascinated mathematicians for centuries. Here are some interesting facts about prime numbers:
Infinity
There are infinitely many prime numbers. This fact was proven by Euclid over 2,300 years ago and is one of the most fundamental results in number theory.
Distribution
The distribution of prime numbers becomes sparser as numbers get larger. The Prime Number Theorem provides an approximation for the distribution of prime numbers.
Largest Known Prime Number
As of today, the largest known prime number is 2^82,589,933 – 1, which has over 24 million digits. It is a Mersenne prime and was discovered in 2018.
Goldbach’s Conjecture
Goldbach’s Conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers. This conjecture remains unproven despite centuries of effort by mathematicians.
Riemann Hypothesis
The Riemann Hypothesis is a conjecture about the distribution of prime numbers and is considered one of the most important unsolved problems in mathematics. It has significant implications for number theory and other areas of mathematics.
FAQs About Prime Numbers
What is a prime number?
A prime number is a whole number greater than 1 that has only two distinct positive divisors: 1 and itself.
Why is 1 not a prime number?
The number 1 is not considered a prime number because it only has one divisor (itself), whereas a prime number must have exactly two distinct divisors.
Is 2 the only even prime number?
Yes, 2 is the only even prime number. All other even numbers are divisible by 2 and therefore have more than two divisors.
What are the first few prime numbers?
The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.
How do you determine if a number is prime?
You can determine if a number is prime by dividing it by all integers from 2 to the square root of the number. If none of these integers divide the number evenly, then it is prime.
What is the Sieve of Eratosthenes?
The Sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to a specified integer. It works by iteratively marking the multiples of each prime, starting with the first prime number, 2.
Are prime numbers finite or infinite?
Prime numbers are infinite. This was proven by Euclid over 2,300 years ago.
What are Mersenne primes?
Mersenne primes are prime numbers that are one less than a power of two. They are of the form 2^n – 1, where n is a prime number.
What are twin primes?
Twin primes are pairs of prime numbers that differ by 2. For example, (3, 5), (5, 7), and (11, 13) are twin primes.
What are some real-world applications of prime numbers?
Prime numbers are used in cryptography, computer science, error correction codes, random number generation, and musical harmony.
What is a composite number?
A composite number is a positive integer that has more than two distinct positive divisors.
What is prime factorization?
Prime factorization is the process of breaking down a number into a product of prime numbers.
What is Goldbach’s Conjecture?
Goldbach’s Conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers.
What is the Riemann Hypothesis?
The Riemann Hypothesis is a conjecture about the distribution of prime numbers and is considered one of the most important unsolved problems in mathematics.
How are prime numbers used in cryptography?
Prime numbers are used in encryption algorithms like RSA, which rely on the difficulty of factoring large composite numbers into their prime factors.
Prime numbers are more than just numbers; they are the building blocks of mathematics and the guardians of our digital security.
Have more questions about prime numbers or any other topic? Don’t hesitate to ask! At WHAT.EDU.VN, we’re dedicated to providing clear, accurate, and accessible answers to all your questions. Our team of experts is here to help you explore the fascinating world of knowledge.
Unlock Your Understanding: Ask Your Questions on WHAT.EDU.VN!
Do you find yourself puzzled by complex topics? Are you searching for clear, reliable answers to your burning questions? Look no further than WHAT.EDU.VN! We understand the challenges of finding trustworthy information quickly and without cost. That’s why we’ve created a platform where you can ask any question and receive expert answers absolutely free.
Why Choose WHAT.EDU.VN?
- Free Access: Ask as many questions as you like without any subscription fees or hidden charges.
- Expert Answers: Our community includes knowledgeable individuals across various fields who are passionate about sharing their expertise.
- Fast Responses: Get the answers you need quickly, so you can keep learning and growing.
- Easy to Use: Our user-friendly interface makes it simple to ask questions and find the information you’re looking for.
- Comprehensive Coverage: No matter what your question is, we’re here to help. From academic subjects to everyday curiosities, we’ve got you covered.
Don’t Let Confusion Hold You Back!
At WHAT.EDU.VN, we believe that everyone deserves access to quality information. Whether you’re a student tackling tough homework, a professional seeking career advice, or simply a curious mind eager to learn, we’re here to support you. Don’t waste time searching through endless websites or worrying about costly consultations. Join our community today and experience the ease and convenience of getting your questions answered for free.
Ready to Get Started?
It’s easy to start asking questions on WHAT.EDU.VN. Simply visit our website, create an account, and post your question. Our community of experts is eager to help you unlock your understanding and achieve your goals.
Contact Us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t wait – ask your question now and discover the power of free, expert answers at what.edu.vn!