Do you want to know what 1/4 is as a decimal? WHAT.EDU.VN provides a simple explanation: 1/4 is equal to 0.25. This article will explore different methods to convert fractions to decimals and offer practical examples. Explore fractions to decimal conversion and equivalent fractions.
1. Understanding What 1/4 Is As A Decimal
The decimal form of (dfrac{1}{4}) is 0.25. When converting a fraction to a decimal, you are expressing it as a number with a denominator of 1, resulting in a decimal value.
2. Converting 1/4 To A Decimal: Step-By-Step
There are two primary methods to convert the fraction (dfrac{1}{4}) into its decimal form:
2.1. Method 1: Long Division
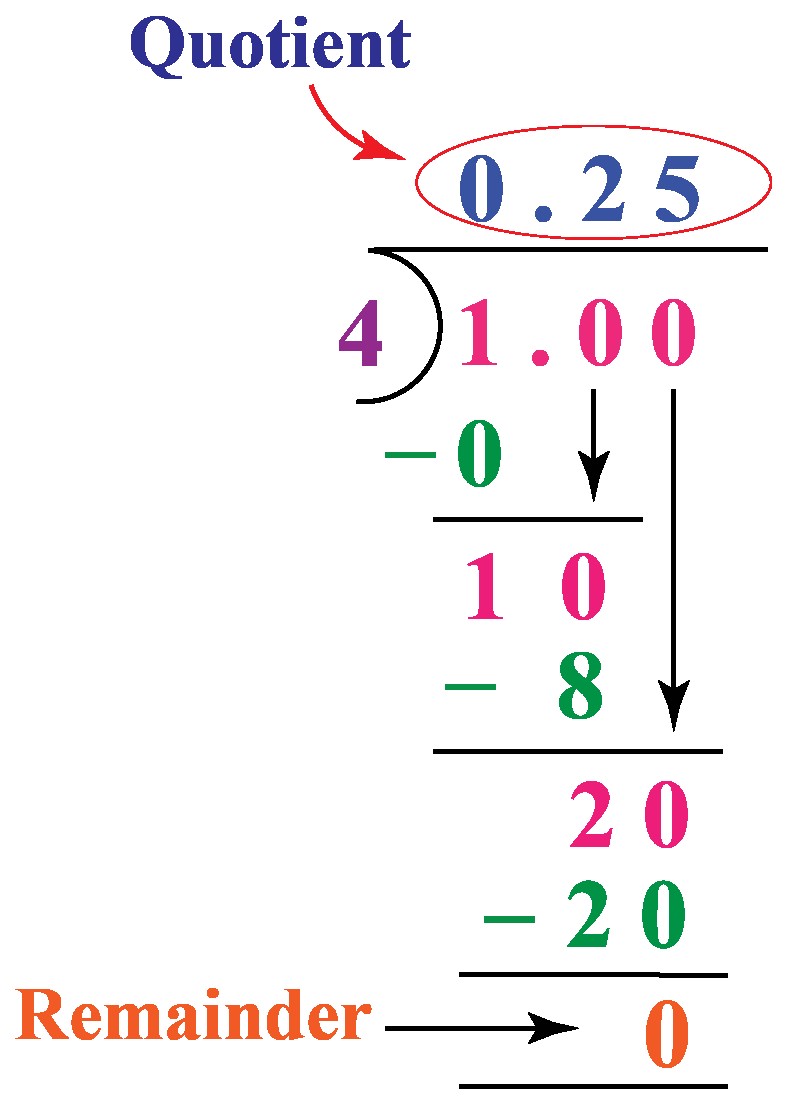
Long division involves dividing the numerator (1) by the denominator (4).
When you divide 1 by 4, the result is 0.25.
(dfrac{1}{4} = 0.25)
This method is applicable for converting any fraction to its decimal equivalent.
2.2. Method 2: Equivalent Fraction With A Denominator Of 10
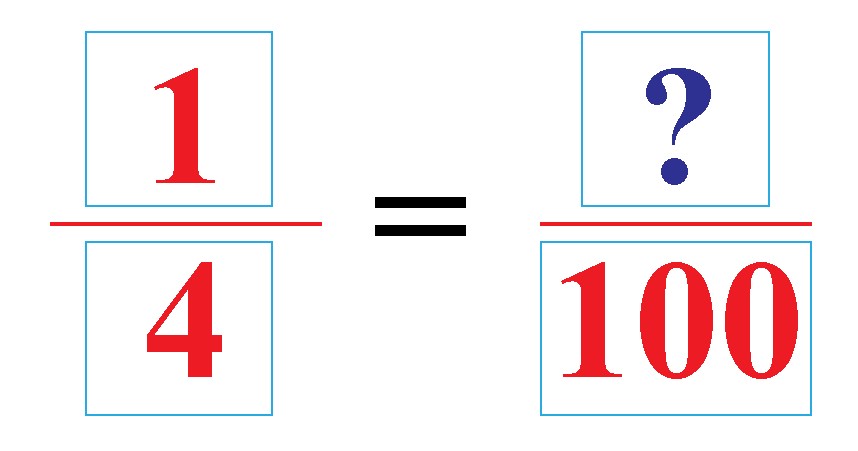
This method involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). In the case of (dfrac{1}{4}), we can convert the denominator to 100.
Since 10 is not a multiple of 4, we look at the next power of 10, which is 100.
To convert the denominator 4 to 100, multiply both the numerator and the denominator by 25:
begin{align} dfrac{1}{4} &= dfrac{1 times 25}{4 times 25} \ &= dfrac{25}{100} end{align}
With 100 as the denominator (two zeros), there will be two digits after the decimal point in the numerator.
(dfrac{1}{4} = 0.25)
This approach can be extended to other fractions. For example, converting (dfrac{3}{8}) to a decimal involves finding an equivalent fraction with a denominator of 1000:
begin{align} dfrac{3}{8} &= dfrac{3 times 125}{8 times 125} \ &= dfrac{375}{1000} \ &= 0.375 end{align}
3. Converting Decimals To Fractions
Converting a decimal to a fraction involves considering the number of digits after the decimal point.
For example, to convert 0.65 to a fraction:
There are two digits after the decimal. Therefore,
begin{align} 0.65 &= dfrac{65}{100} \ &= dfrac{13}{20} end{align}
4. Key Points To Remember
- Decimals represent fractions with values less than 1.
- Visual representation of 0.25 on a number line:
5. Solved Examples
5.1. Example 1: Converting 2/3 To Decimal
Question: Harry is having trouble expressing (dfrac{2}{3}) as a decimal. Can you help him convert the fraction to a decimal using long division?
Solution:
Since the denominator is 3, which is not a factor of 100, we will convert (dfrac{2}{3}) to a decimal using long division.
The quotient is 0.6666….. = (0.overline{6}). The digit 6 recurs because the remainder repeats.
Rounding off 0.6666….. to two decimal places gives us 0.67.
| (thereforedfrac{2}{3} = 0.67) |
|---|
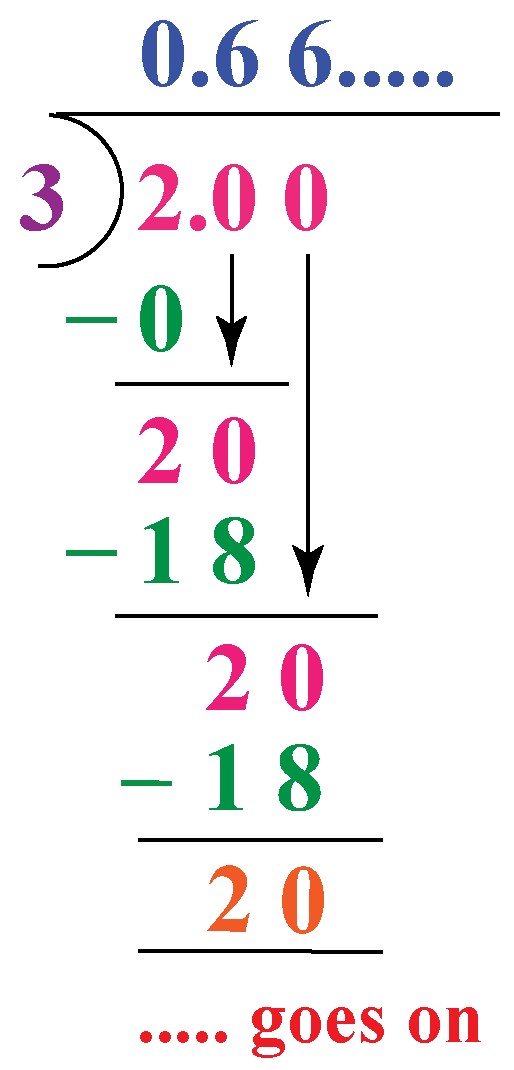
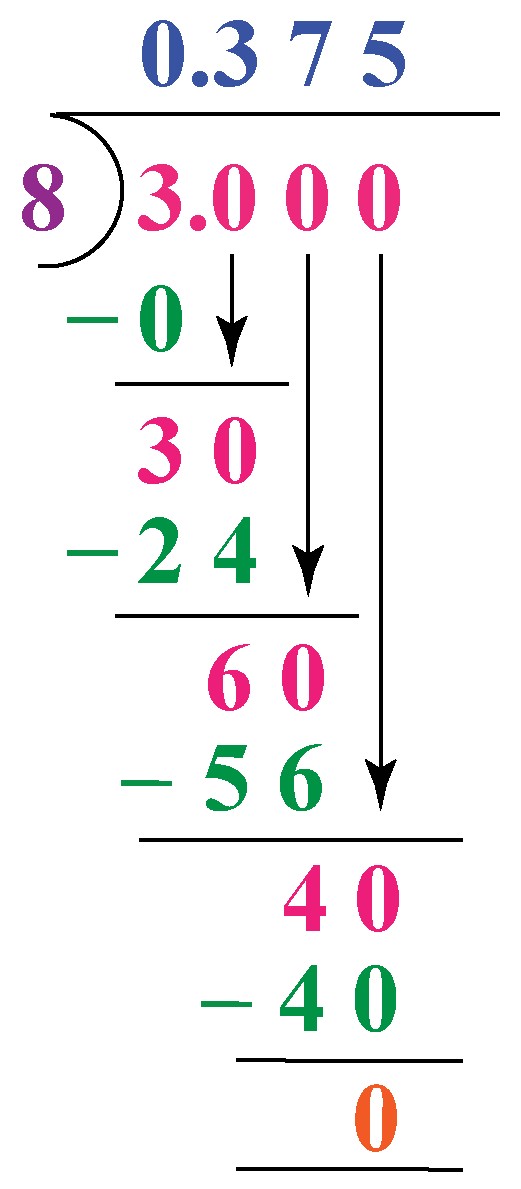
5.2. Example 2: Converting 3/8 To Decimal
Question: Mia wants to express (dfrac{3}{8}) as a decimal number using long division. Help her find the correct answer.
Solution:
Mia needs to divide 3 by 8 and continue dividing until she gets a remainder of 0.
| (therefore) The decimal form of (dfrac{3}{8}) is 0.375 |
|---|
6. Additional Fraction To Decimal Examples
Understanding how to convert fractions to decimals can be further solidified by looking at more examples. Let’s explore (dfrac{1}{5}), (dfrac{1}{6}), (dfrac{1}{7}), (dfrac{1}{9}), and (dfrac{2}{5}) as decimals. This section will provide step-by-step conversions to help you grasp the process and apply it to various fractions.
6.1. Converting 1/5 to a Decimal
To convert (dfrac{1}{5}) to a decimal, you can use either long division or find an equivalent fraction with a denominator of 10. In this case, it’s easiest to convert to a fraction with a denominator of 10.
Multiply both the numerator and denominator by 2:
begin{align} dfrac{1}{5} &= dfrac{1 times 2}{5 times 2} \ &= dfrac{2}{10} \ &= 0.2 end{align}
So, (dfrac{1}{5}) as a decimal is 0.2.
6.2. Converting 1/6 to a Decimal
Converting (dfrac{1}{6}) to a decimal requires long division since 6 is not a factor of 10 or 100.
When you perform the long division of 1 ÷ 6, you get a repeating decimal:
(dfrac{1}{6} = 0.1666…)
This is often written as (0.1overline{6}), where the line over the 6 indicates that it repeats indefinitely.
Rounding to two decimal places, (dfrac{1}{6} approx 0.17).
6.3. Converting 1/7 to a Decimal
Converting (dfrac{1}{7}) to a decimal also involves long division. The decimal representation of (dfrac{1}{7}) is a repeating decimal:
(dfrac{1}{7} = 0.142857142857…)
The digits 142857 repeat indefinitely. This can be written as (0.overline{142857}).
Rounding to two decimal places, (dfrac{1}{7} approx 0.14).
6.4. Converting 1/9 to a Decimal
To convert (dfrac{1}{9}) to a decimal, perform long division. The result is a repeating decimal:
(dfrac{1}{9} = 0.1111…)
This is written as (0.overline{1}), indicating that the digit 1 repeats indefinitely.
So, (dfrac{1}{9}) as a decimal is approximately 0.11 when rounded to two decimal places.
6.5. Converting 2/5 to a Decimal
Converting (dfrac{2}{5}) to a decimal can be done by finding an equivalent fraction with a denominator of 10.
Multiply both the numerator and the denominator by 2:
begin{align} dfrac{2}{5} &= dfrac{2 times 2}{5 times 2} \ &= dfrac{4}{10} \ &= 0.4 end{align}
Thus, (dfrac{2}{5}) as a decimal is 0.4.
7. Think Out Of The Box
Find the decimal forms of the fractions (dfrac{1}{5}) and (dfrac{1}{7}). What difference do you notice in their decimal forms?
(Hint: Observe the remainders in both cases.)
8. Interactive Questions
Test your knowledge with these interactive questions. Select/Type your answer and click the “Check Answer” button to see the result.
9. Fraction To Decimal Conversion Table
| Fraction | Decimal | Conversion Method |
|---|---|---|
| 1/2 | 0.5 | 1 ÷ 2 |
| 1/3 | 0.333… | 1 ÷ 3 |
| 1/4 | 0.25 | 1 ÷ 4 |
| 1/5 | 0.2 | 1 ÷ 5 |
| 1/6 | 0.166… | 1 ÷ 6 |
| 1/7 | 0.142857… | 1 ÷ 7 |
| 1/8 | 0.125 | 1 ÷ 8 |
| 1/9 | 0.111… | 1 ÷ 9 |
| 1/10 | 0.1 | 1 ÷ 10 |
| 2/3 | 0.666… | 2 ÷ 3 |
| 2/5 | 0.4 | 2 ÷ 5 |
| 3/4 | 0.75 | 3 ÷ 4 |
| 3/5 | 0.6 | 3 ÷ 5 |
| 4/5 | 0.8 | 4 ÷ 5 |
| 5/6 | 0.833… | 5 ÷ 6 |
This table provides a quick reference for common fractions and their decimal equivalents, reinforcing the methods discussed for converting fractions to decimals.
10. Real-World Applications Of Fraction And Decimal Conversion
Understanding how to convert fractions to decimals and vice versa is crucial in many real-world scenarios. Here are some examples:
10.1. Cooking And Baking
In cooking, recipes often use fractions to represent ingredient quantities. For instance, a recipe might call for (dfrac{1}{4}) cup of sugar or (dfrac{1}{2}) teaspoon of salt. Converting these fractions to decimals can help with precise measurements, especially when using digital scales that display measurements in decimal form. Knowing that (dfrac{1}{4}) cup is equal to 0.25 cup allows for accurate measuring, ensuring the dish turns out as intended.
10.2. Financial Calculations
In finance, decimals and fractions are frequently used to represent interest rates, stock prices, and other financial metrics. For example, an interest rate might be expressed as 4.5% or 0.045 in decimal form. Understanding these conversions is essential for calculating returns on investments, understanding loan terms, and managing personal finances effectively. Stock prices are often quoted in decimals, and converting these to fractions can provide a clearer understanding of price movements.
10.3. Construction And Engineering
In construction and engineering, precise measurements are critical. Fractions and decimals are used interchangeably to represent lengths, areas, and volumes. For example, a blueprint might specify a length of 3 (dfrac{1}{2}) inches. Converting this to 3.5 inches makes it easier to use with measuring tools that display decimal values. Accurate conversions ensure that structures are built according to specifications, avoiding costly errors and ensuring safety.
10.4. Retail And Sales
Retailers often use decimals to represent prices and discounts. For example, an item might be priced at $19.99, or a discount might be advertised as 25% off. Converting these percentages to decimals helps customers calculate the actual savings and the final price of the item. Understanding these conversions ensures transparency and helps consumers make informed purchasing decisions.
10.5. Academic Studies
In academic settings, particularly in mathematics and science, understanding fraction and decimal conversions is fundamental. Students encounter fractions and decimals in various contexts, from solving algebraic equations to performing scientific calculations. Being able to convert between these forms fluently is essential for success in these subjects. For example, converting fractions to decimals can simplify complex calculations and make it easier to compare values.
10.6. Everyday Problem Solving
Even in everyday situations, the ability to convert fractions to decimals can be useful. For example, when splitting a bill with friends, you might need to calculate (dfrac{1}{3}) of the total amount. Knowing that (dfrac{1}{3}) is approximately 0.333 allows you to quickly estimate your share. Similarly, when planning a road trip, you might need to calculate distances using a map that provides measurements in both fractions and decimals.
11. Exploring Different Types Of Decimals
Decimals come in various forms, each with its unique characteristics. Understanding these different types is essential for working with numbers effectively. Here are the primary categories of decimals:
11.1. Terminating Decimals
Terminating decimals are decimals that have a finite number of digits. In other words, they come to an end. Examples of terminating decimals include:
- 0.5 (which is (dfrac{1}{2}))
- 0.25 (which is (dfrac{1}{4}))
- 0.125 (which is (dfrac{1}{8}))
- 3.75 (which is 3 (dfrac{3}{4}))
Terminating decimals can be easily converted into fractions with a power of 10 as the denominator.
11.2. Repeating Decimals
Repeating decimals, also known as recurring decimals, have a digit or a group of digits that repeat indefinitely. The repeating part is often indicated by a line (vinculum) over the repeating digits. Examples of repeating decimals include:
- 0.333… (which is (dfrac{1}{3}), often written as (0.overline{3}))
- 0.666… (which is (dfrac{2}{3}), often written as (0.overline{6}))
- 0.142857142857… (which is (dfrac{1}{7}), often written as (0.overline{142857}))
- 1.232323… (which is 1 (dfrac{23}{99}), often written as (1.overline{23}))
Repeating decimals can be converted into fractions, although the process is a bit more complex than with terminating decimals.
11.3. Non-Terminating Non-Repeating Decimals
Non-terminating non-repeating decimals are decimals that go on forever without any repeating pattern. These numbers cannot be expressed as a fraction of two integers and are known as irrational numbers. Examples of non-terminating non-repeating decimals include:
- π (pi), approximately 3.141592653589793…
- √2 (square root of 2), approximately 1.414213562373095…
- e (Euler’s number), approximately 2.718281828459045…
These numbers are fundamental in mathematics and have significant applications in various fields.
11.4. Mixed Decimals
Mixed decimals combine a whole number with a decimal part. These can be terminating, repeating, or non-terminating non-repeating. Examples of mixed decimals include:
- 3.5 (3 (dfrac{1}{2}), terminating)
- 2.666… (2 (dfrac{2}{3}), repeating)
- 5.14159… (5 + π – 3, non-terminating non-repeating)
12. How To Convert Repeating Decimals To Fractions
Converting repeating decimals to fractions involves a specific process that allows you to express the decimal as a ratio of two integers. Here’s how to convert repeating decimals to fractions:
12.1. Converting a Simple Repeating Decimal to a Fraction
Let’s convert (0.overline{3}) to a fraction.
-
Set up an equation: Let x = (0.overline{3}).
-
Multiply by 10: Multiply both sides by 10 to shift the decimal point one place to the right: 10x = 3.(overline{3}).
-
Subtract the original equation: Subtract the original equation (x = (0.overline{3})) from the new equation (10x = 3.(overline{3})):
10x – x = 3.(overline{3}) – (0.overline{3})
9x = 3
-
Solve for x: Divide both sides by 9 to solve for x:
x = (dfrac{3}{9}) = (dfrac{1}{3})
Thus, (0.overline{3}) = (dfrac{1}{3}).
12.2. Converting a Repeating Decimal With Multiple Repeating Digits to a Fraction
Let’s convert (0.overline{23}) to a fraction.
-
Set up an equation: Let x = (0.overline{23}).
-
Multiply by 100: Since two digits repeat, multiply both sides by 100 to shift the decimal point two places to the right: 100x = 23.(overline{23}).
-
Subtract the original equation: Subtract the original equation (x = (0.overline{23})) from the new equation (100x = 23.(overline{23})):
100x – x = 23.(overline{23}) – (0.overline{23})
99x = 23
-
Solve for x: Divide both sides by 99 to solve for x:
x = (dfrac{23}{99})
Thus, (0.overline{23}) = (dfrac{23}{99}).
12.3. Converting a Repeating Decimal With Non-Repeating Digits to a Fraction
Let’s convert 0.1(overline{6}) to a fraction.
-
Set up an equation: Let x = 0.1(overline{6}).
-
Multiply by 10: Multiply both sides by 10 to move the non-repeating digit to the left of the decimal point: 10x = 1.(overline{6}).
-
Multiply by 100: Multiply both sides by 100 to move one repeating digit to the left of the decimal point: 100x = 16.(overline{6}).
-
Subtract the equations: Subtract the equation 10x = 1.(overline{6}) from the equation 100x = 16.(overline{6}):
100x – 10x = 16.(overline{6}) – 1.(overline{6})
90x = 15
-
Solve for x: Divide both sides by 90 to solve for x:
x = (dfrac{15}{90}) = (dfrac{1}{6})
Thus, 0.1(overline{6}) = (dfrac{1}{6}).
13. Advanced Tips For Working With Decimals And Fractions
Working with decimals and fractions efficiently often requires a few advanced techniques. Here are some tips to help you handle more complex scenarios:
13.1. Simplifying Fractions Before Converting
Before converting a fraction to a decimal, simplify it to its lowest terms. This makes the conversion process easier and reduces the chances of errors. For example, instead of converting (dfrac{4}{16}) directly, simplify it to (dfrac{1}{4}) first, then convert to 0.25.
13.2. Using Prime Factorization
Prime factorization can help determine whether a fraction will result in a terminating or repeating decimal. If the denominator of the simplified fraction only contains the prime factors 2 and 5, the decimal will terminate. Otherwise, it will repeat. For example:
- (dfrac{3}{20}) has a denominator of 20 = 2^2 * 5, so it will terminate (0.15).
- (dfrac{5}{12}) has a denominator of 12 = 2^2 * 3, so it will repeat (0.41(overline{6})).
13.3. Approximating Decimals
In many practical situations, it is sufficient to approximate decimals to a certain number of decimal places. Rounding rules are essential for this:
- If the next digit is 5 or greater, round up the last digit.
- If the next digit is less than 5, keep the last digit as is.
For example, rounding 3.14159 to two decimal places gives 3.14.
13.4. Converting Mixed Numbers
To convert a mixed number to a decimal, convert the fractional part to a decimal and add it to the whole number. For example, to convert 4 (dfrac{3}{8}) to a decimal:
- (dfrac{3}{8}) = 0.375
- 4 + 0.375 = 4.375
13.5. Estimation Techniques
Developing estimation skills can help you quickly check the reasonableness of your answers. For example, if you are converting (dfrac{7}{16}) to a decimal, you can estimate that it is a little less than (dfrac{1}{2}), so the decimal should be a bit less than 0.5. The actual value is 0.4375, which aligns with the estimate.
13.6. Understanding Decimal Place Values
A solid understanding of decimal place values is crucial for accurate calculations. Each position to the right of the decimal point represents a fraction with a power of 10 as the denominator:
- Tenths (0.1)
- Hundredths (0.01)
- Thousandths (0.001)
- Ten-thousandths (0.0001)
Recognizing these place values helps in converting decimals to fractions and performing arithmetic operations.
14. Frequently Asked Questions (FAQs)
14.1. What is (dfrac{1}{8}) as a decimal?
The decimal form of (dfrac{1}{8}) = 0.125.
14.2. What is (dfrac{9}{20}) as a decimal?
The decimal form of (dfrac{9}{20}) = 0.45.
14.3. How do you write (dfrac{1}{3}) as a decimal?
(dfrac{1}{3}) can be written in decimal form as 0.333333…. (never ending), which can be rounded off to 0.33.
15. Need More Help?
We hope you enjoyed learning about 1/4 as a decimal with the explanations and examples. Now, you should be able to easily solve problems involving 3/8 as a decimal, 2/3 as a decimal, and decimal to fraction conversions.
If you still have questions or need further clarification, don’t hesitate to ask! At WHAT.EDU.VN, we are dedicated to providing clear and helpful explanations to make learning easier for you. Whether you’re struggling with fractions, decimals, or any other math concept, we’re here to help.
Do you have a question that wasn’t covered in this article? Visit WHAT.EDU.VN today and ask your question for free! Our community of experts is ready to provide you with quick and accurate answers.
Contact Us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Don’t struggle alone – let what.edu.vn be your go-to resource for all your questions!