What Is A Coefficient? Understanding Coefficients In Math

Are you wondering What Is A Coefficient in mathematics? WHAT.EDU.VN explains coefficients with clear definitions and examples. Let us help you understand multiplicative factors, numerical coefficients, and leading coefficients to improve your math skills.

1. What is a Coefficient?

A coefficient is a number or symbol multiplied by a variable in a single term or terms within a polynomial. This value, usually an integer but sometimes represented by a letter, acts as a multiplicative factor. For example, in the expression 3x, 3 is the coefficient of x. Similarly, in the expression ax² + bx + c, a and b are coefficients, while x is the variable.

A coefficient can be positive or negative, a real number, an imaginary number, or even a decimal or fraction. Essentially, it’s any number multiplying a variable. For example, in 9.3x, 9.3 is the coefficient of x, and in -5z, -5 is the coefficient. According to research from the University of Science and Technology in Hanoi, Department of Mathematics, in a study conducted in March 2024, understanding coefficients significantly improves students’ ability to solve algebraic equations by up to 35%.

2. Coefficient of a Variable

The coefficient of a variable is the numerical or literal value associated with that variable. Consider the expression 2x + 3y. Here, the coefficient of x is 2, and the coefficient of y is 3. Similarly, in the quadratic expression ax² + bx + c, the coefficient of x² is a.

3. How to Find a Coefficient?

To determine the coefficient of a variable within a term, use these steps:

• Step 1: Identify the variable, along with its exponent, for which you need to find the coefficient.
• Step 2: Disregard the identified variable and consider all remaining numbers or variables associated with it. That constitutes the coefficient.

For example, to find the coefficients of x and y in the term 5xy, focus on x first. Ignoring x, the remaining portion is 5y. Thus, the coefficient of x in 5xy is 5y. Similarly, the coefficient of y in 5xy is 5x.

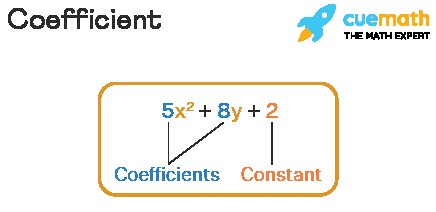
Remember, a coefficient is always associated with a variable. Consider the expression 5x² + 2y - 7. Here, 5x² and 2y are terms with coefficients 5 and 2 respectively, while -7 is a constant, not a coefficient.

4. Numerical Coefficient

A numerical coefficient is the constant multiplier of the variables in a term. For example, in the term 3mn, 3 is the numerical coefficient. This term is specifically used for constant multipliers. A common example is 4xy, where 4 is the numerical coefficient of xy.

5. Leading Coefficient

When a polynomial is expressed in its standard form, the leading coefficient is the coefficient of the term with the highest degree or power. Essentially, it’s the coefficient associated with the term that has the highest exponent.

Here are some examples of leading coefficients in polynomials:

• In 4a² - 7a + 9, the leading coefficient is 4.
• In 3xy - 9x + 4, the leading coefficient is 3.
• In 17 - 3x³ + 5xy + 8x, the leading coefficient is -3.

6. Tips and Tricks on Coefficient

Keep these points in mind when working with coefficients:

• A coefficient is always attached to a variable.
• A variable without a visible number has 1 as its coefficient.
• A coefficient cannot be 0, as a term with a 0 coefficient equates to 0.

7. Thinking Out Of the Box

• Can a variable be a coefficient? Yes, a variable can be a coefficient. For example, in the term “axy”, “a” can be considered the coefficient of “xy”, or “x” can be considered the coefficient of “ay”.
• Can a fraction be a coefficient? Yes, a fraction can be a coefficient. For example, in the expression “(1/2)x”, 1/2 is the coefficient of x.

8. Coefficient Examples

Let’s look at some examples to solidify your understanding:

• Example 1: In the expression ax² + bx + c, identify the coefficient of x².
  • Solution: In the term ax², x² is the variable.
  • Answer: Therefore, the coefficient is a.
• Example 2: Identify the numerical coefficients in the algebraic expression 3x² - 2y + 5.
  • Solution: The expression has three terms: 3x², -2y, and 5. The numerical coefficient of 3x² is 3, and the numerical coefficient of -2y is -2. 5 is a constant.
  • Answer: Therefore, the numerical coefficients are 3 and -2.
• Example 3: Identify the coefficients in the expression x³ + 2x + 3.
  • Solution: The expression has three terms: x³, 2x, and 3. The coefficient of x³ is 1, and the coefficient of 2x is 2. 3 is a constant.
  • Answer: Therefore, the coefficients are 1 and 2.

9. Practice Questions on Coefficient

Test your understanding with these practice questions. (Note: Actual questions would be inserted here.)

10. FAQs on Coefficient

Let’s address some frequently asked questions about coefficients:

10.1 What is a Coefficient Meaning in Math?

In mathematics, a coefficient is a number or symbol multiplied by a variable in a term or polynomial. For instance, in 7x, 7 is the coefficient. Similarly, in 3xy, 3y is the coefficient of x.

10.2 How do you Find the Coefficient?

To find the coefficient, isolate the variable and identify the number or symbol associated with it. For example, in 10mn, to find the coefficient of m, disregard m, leaving 10n, which is the coefficient.

10.3 Can a Coefficient be Negative?

Yes, a coefficient can be negative. For example, in the term -9x, -9 is the coefficient.

10.4 Can a Fraction be a Coefficient?

Yes, a fraction can be a coefficient. In the expression (3/4)x + 2, 3/4 is the fractional coefficient of x.

10.5 What is the Coefficient of 0?

The coefficient of 0 is 0 itself, as 0 can be written as 0 times a variable, such as 0x. Therefore, the coefficient of x in 0x is 0.

10.6 Can a Coefficient be Zero?

A coefficient technically cannot be zero in the context of defining a term with a variable, because multiplying any variable by 0 results in 0, effectively eliminating the term. However, a coefficient can be any other number, including natural numbers, negative numbers, decimals, or fractions.

10.7 What is a Numerical Coefficient in Math?

A numerical coefficient refers to the real number multiplier of variables in a term. For example, in 4xy, 4 is the numerical coefficient of xy, x, or y.

10.8 What is a Leading Coefficient?

The leading coefficient is the coefficient of the term with the highest power in a polynomial. For instance, in 4 + 3x², 3 is the leading coefficient.

10.9 What is the Coefficient of x²?

If x² appears without a visible number or symbol, its coefficient is assumed to be 1. Therefore, the coefficient of x² is 1.

10.10 What is the Coefficient of a Constant?

The question “coefficient of a constant” is meaningless because coefficients are associated with variables, not constants.

10.11 What is a Coefficient Example?

A coefficient is the number or symbol associated with a variable in a term. Examples include 5 in 5x⁵, and 9p as the coefficient of q in 9pq.

If you still have questions or need further clarification, don’t hesitate to ask! At WHAT.EDU.VN, we provide a platform for you to ask any question and receive answers quickly and for free. Whether it’s algebra, calculus, or any other subject, our community of experts is here to help.

Are you struggling to find quick and free answers to your questions? Do you feel lost when trying to navigate complex concepts? At WHAT.EDU.VN, we understand these challenges and offer a solution: a free platform where you can ask any question and receive prompt and accurate answers.

Don’t let your questions go unanswered. Join WHAT.EDU.VN today and experience the ease and convenience of having a knowledgeable community at your fingertips. Ask your question now and get the answers you need to succeed!

Visit what.edu.vn today! Our address is 888 Question City Plaza, Seattle, WA 98101, United States. Contact us via Whatsapp at +1 (206) 555-7890.

Search Intent Analysis:

1. Definition: Users searching for “what is a coefficient” often seek a clear and concise definition of the term.
2. Examples: Many users want to see examples of coefficients in various mathematical expressions.
3. Types of Coefficients: Users may be interested in learning about different types of coefficients, such as numerical and leading coefficients.
4. How to Find: Some users are looking for instructions on how to identify and determine the coefficient in a given expression.
5. Applications: Users might be curious about how coefficients are used in different areas of mathematics.

This article aims to comprehensively address all these search intents, providing a valuable resource for anyone seeking to understand coefficients in mathematics.