Are you wondering What Is A Coefficient In Math? A coefficient is a number or symbol multiplied by a variable in an algebraic term, and at WHAT.EDU.VN, we break down this concept into easy-to-understand explanations. We offer comprehensive, clear answers, so you can confidently tackle mathematical problems involving coefficients. Dive in to master coefficients and explore related mathematical concepts with us, and don’t hesitate to ask your own questions for free.
1. Understanding Coefficients
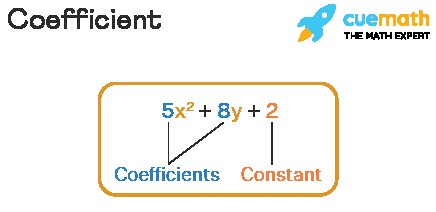
A coefficient in mathematics is a number or symbol that multiplies a variable in a single term or within the terms of a polynomial expression. It’s typically a numerical value, but can also be represented by a letter or symbol that stands for a constant. For instance, in the expression ax² + bx + c, ‘a’ and ‘b’ are the coefficients of the variables x² and x, respectively, while ‘c’ is a constant.
Coefficients can be positive, negative, real, imaginary, or expressed as decimals or fractions. Essentially, a coefficient is the factor that determines the quantity of a variable in a mathematical expression.
2. Exploring Variable Coefficients
The coefficient of a variable is the numerical or symbolic value that’s associated with a specific variable in an algebraic expression. It indicates how many units of the variable are included in the term. For example, in the expression 3x + 4y, the coefficient of the variable x is 3, and the coefficient of the variable y is 4.
In a quadratic expression like ax² + bx + c, the coefficient of the x² term is ‘a’, and the coefficient of the x term is ‘b’. Understanding variable coefficients is vital for simplifying expressions, solving equations, and analyzing mathematical relationships.
3. How To Find A Coefficient: A Step-by-Step Guide
Finding the coefficient of a variable in a term involves a straightforward process:
3.1. Identify the Variable
Locate the variable for which you want to find the coefficient.
3.2. Isolate the Term
Focus on the term that contains the variable of interest.
3.3. Determine the Multiplier
Identify the number or symbol that is multiplying the variable. This multiplier is the coefficient.
For example, in the term 7xy, to find the coefficient of x, isolate the term and identify what multiplies x, which is 7y. Therefore, the coefficient of x in the term 7xy is 7y. Similarly, the coefficient of y in 7xy is 7x.
Remember, the coefficient is always associated with a variable. In an expression like 4x² + 5y – 9, the terms are 4x², 5y, and -9. The coefficients are 4 and 5, respectively, while -9 is a constant.
4. Decoding Numerical Coefficients
A numerical coefficient is the constant number that multiplies the variables in a term. It’s a real number that gives the term its quantitative value.
4.1. Examples of Numerical Coefficients
- In the term 6mn, 6 is the numerical coefficient.
- In the term -2.5ab², -2.5 is the numerical coefficient.
- In the term (2/3)pqr, 2/3 is the numerical coefficient.
Numerical coefficients play a crucial role in determining the magnitude and direction (positive or negative) of a term’s contribution to an expression.
5. Leading Coefficient: What It Is and Why It Matters
The leading coefficient is the coefficient of the term with the highest degree in a polynomial when the polynomial is written in standard form. The standard form of a polynomial is written with the term with the highest power first, followed by the terms with decreasing powers.
5.1. Identifying the Leading Coefficient
- Arrange the polynomial in standard form.
- Identify the term with the highest power of the variable.
- The coefficient of that term is the leading coefficient.
5.2. Examples of Leading Coefficients
- In the polynomial 5x³ – 2x² + x – 7, the leading coefficient is 5.
- In the polynomial 8 – 3x + 4x², the leading coefficient is 4 (after rearranging as 4x² – 3x + 8).
- In the polynomial -x⁴ + 6x³ – 2x + 1, the leading coefficient is -1.
The leading coefficient provides important information about the end behavior of a polynomial function, which is valuable in graphing and analyzing polynomials.
6. Tips And Tricks: Mastering Coefficients
When working with coefficients, keep the following points in mind:
6.1. Association with Variables
A coefficient is always attached to a variable. If a term has a variable without an explicit number, the coefficient is assumed to be 1.
6.2. Non-Zero Coefficient
A coefficient cannot be zero because a term with a zero coefficient has a value of zero, effectively eliminating the variable from the expression.
6.3. Variables as Coefficients
Variables can indeed act as coefficients. In expressions like axy, a can be considered the coefficient of xy.
6.4. Fractional Coefficients
Fractions are also valid coefficients. In the expression (1/2)x, 1/2 is the coefficient of x.
7. Coefficient Examples: Putting Knowledge into Practice
7.1. Example 1: Simple Algebraic Expression
In the expression 5x² + 3x – 2, identify the coefficients.
- The coefficient of x² is 5.
- The coefficient of x is 3.
- -2 is a constant.
7.2. Example 2: Identifying Numerical Coefficients
In the expression 7ab – 4c + 9, identify the numerical coefficients.
- The numerical coefficient of ab is 7.
- The numerical coefficient of c is -4.
7.3. Example 3: Polynomial Expression
In the polynomial 3x⁴ – 2x³ + x² + 5x – 1, identify the leading coefficient.
- The leading coefficient is 3.
8. Practice Questions: Test Your Knowledge
8.1. Question 1
What are the coefficients in the expression 2y³ – 5y + 8?
8.2. Question 2
Identify the leading coefficient in the polynomial -4x⁵ + 3x² – x + 2
8.3. Question 3
In the term 1/4xyz, what is the coefficient of yz?
Test your understanding and reinforce your skills with these practice questions.
9. Real-World Applications of Coefficients
Coefficients aren’t just abstract mathematical concepts; they have numerous practical applications in various fields:
9.1. Physics
In physics, coefficients appear in equations describing physical phenomena. For example, the coefficient of friction is used to calculate the frictional force between two surfaces. The drag coefficient is used to determine the resistance of an object moving through a fluid.
9.2. Engineering
Engineers use coefficients extensively in structural analysis, fluid dynamics, and electrical engineering. For instance, in structural analysis, coefficients of thermal expansion are used to calculate how materials expand or contract with temperature changes.
9.3. Economics
In economics, coefficients appear in regression models and equations. For example, in a demand equation, the price elasticity of demand is a coefficient that measures the responsiveness of the quantity demanded to a change in price.
9.4. Computer Science
In computer science, coefficients are used in machine learning algorithms and data analysis. For instance, in linear regression, coefficients represent the weights assigned to different features in the model.
10. Advanced Topics: Beyond the Basics
10.1. Correlation Coefficient
The correlation coefficient is a statistical measure that quantifies the strength and direction of a linear relationship between two variables. It ranges from -1 to +1, where:
- +1 indicates a perfect positive correlation.
- -1 indicates a perfect negative correlation.
- 0 indicates no linear correlation.
The correlation coefficient is widely used in data analysis, finance, and other fields to understand how variables relate to each other.
10.2. Binomial Coefficients
Binomial coefficients are the coefficients of the terms in the expansion of a binomial expression like (a + b)^n. They are denoted as “n choose k” or C(n, k) and can be calculated using the formula:
C(n, k) = n! / (k! * (n - k)!)where n! represents the factorial of n. Binomial coefficients are essential in combinatorics, probability theory, and various areas of mathematics.
11. Coefficient FAQs: Your Questions Answered
11.1. What Is a Coefficient Meaning In Math?
A coefficient is a number or symbol that multiplies a variable in an algebraic term. For instance, in the term 5x, 5 is the coefficient. In the term 2ab, 2 is the coefficient of ab.
11.2. How Do You Find the Coefficient?
To find the coefficient, identify the variable and determine the number or symbol that multiplies it. For example, to find the coefficient of y in the term 8yz, isolate y, and you’re left with 8z, which is the coefficient.
11.3. Can a Coefficient Be Negative?
Yes, a coefficient can be negative. For example, in the term -3x, -3 is the coefficient.
11.4. Can a Fraction Be a Coefficient?
Yes, a fraction can be a coefficient. In the expression (1/4)x + 2, 1/4 is the coefficient of x.
11.5. What Is the Coefficient of 0?
The coefficient of 0 is 0 itself, as 0 can be written as 0 multiplied by any variable (e.g., 0x). Thus, the coefficient of x in 0x is 0.
11.6. Can a Coefficient Be Zero?
A coefficient cannot be zero in the context of leaving a variable present because when 0 is multiplied by any variable, the term becomes 0, effectively removing the variable. However, a coefficient can be any natural number, negative number, decimal, or fraction.
11.7. What Is a Numerical Coefficient in Math?
A numerical coefficient is a constant real number that multiplies the variables in a term. For example, in the term 7xyz, the numerical coefficient of xyz, x, y, or z is 7.
11.8. What Is a Leading Coefficient?
The leading coefficient is the coefficient of the term with the highest power in a polynomial. For example, in the expression 6 + 5x², 5 is the leading coefficient.
11.9. What Is the Coefficient of x²?
The coefficient of a variable with no explicit number or symbol attached is always 1. So, the coefficient of x² is 1.
11.10. What Is the Coefficient of a Constant?
The question “coefficient of a constant” doesn’t apply because the term “coefficient” is only relevant when there is a variable present.
11.11. What Is a Coefficient Example?
A coefficient is a number or symbol associated with a variable in a term. Examples include:
- The coefficient of x in 6x is 6.
- The coefficient of p in 3pq is 3q.
Do you still have burning questions about coefficients? At WHAT.EDU.VN, we’re here to provide quick and cost-free answers to all your queries. With our platform, asking questions is simple, and getting reliable answers is even simpler.
12. Let’s Summarize
Understanding coefficients is essential for success in algebra and beyond. From identifying coefficients in simple expressions to working with leading coefficients in polynomials, this comprehensive guide has covered the key concepts, provided examples, and answered frequently asked questions.
By mastering coefficients, you’ll be well-equipped to tackle a wide range of mathematical problems and applications. Remember, coefficients are the building blocks of algebraic expressions and equations, and understanding them will unlock new levels of mathematical proficiency.
13. Take Action Now: Ask Your Questions on WHAT.EDU.VN
Still puzzled about some math concepts? Need clarification on a specific problem? Don’t worry—WHAT.EDU.VN is here to assist you. We understand the difficulties students face when trying to find quick, reliable answers to their questions. That’s why we’ve created a platform where you can ask any question and receive prompt, accurate responses from knowledgeable individuals.
13.1. Why Choose WHAT.EDU.VN?
- Free to Use: Ask as many questions as you need without any cost.
- Quick Answers: Get timely responses to keep your learning on track.
- Expert Assistance: Connect with experienced individuals who can provide clear, understandable explanations.
- Easy to Use: Our platform is designed for simplicity and ease of navigation.
13.2. How It Works
- Visit WHAT.EDU.VN.
- Submit your question in the query box.
- Receive answers from our community of experts.
13.3. Don’t Stay Confused—Get Clarity Today
Why struggle in silence when you can easily find the answers you need? WHAT.EDU.VN is your go-to resource for all your questions. Whether it’s a simple equation or a complex concept, we’re here to help.
Take the next step in your educational journey and experience the convenience of having your questions answered quickly and accurately. Join the many students who have already discovered the benefits of WHAT.EDU.VN.
13.4. Contact Us
For any inquiries or assistance, feel free to reach out to us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Stop struggling with your homework and start getting the answers you deserve. Ask your questions on what.edu.vn today and unlock your full academic potential!