Composite Number: Understand its definition, properties, and uses with WHAT.EDU.VN. Unlock knowledge of composite numbers with prime factorization and number theory. Discover the simplicity of mathematics!
Are you curious about numbers that have more than just two factors? At WHAT.EDU.VN, we demystify mathematical concepts and provide clear explanations. Learn about composite numbers, their properties, and how they differ from prime numbers. Eager to understand number composition?
1. Defining Composite Numbers: What Are They?
Composite numbers are positive integers that can be formed by multiplying two smaller positive integers. This means they have more than two factors: 1, themselves, and at least one other number. Understanding composite numbers involves grasping key concepts in number theory and prime factorization.
1.1. Understanding the Composite Number Definition
A composite number is a natural number greater than 1 that is not a prime number. In simpler terms, it’s a number that can be divided evenly by numbers other than 1 and itself. This divisibility makes composite numbers fundamental in various mathematical applications.
1.2. The Meaning of Composite Number Explained
The term “composite” signifies that these numbers are composed of smaller factors. For instance, 6 is a composite number because it is divisible by 1, 2, 3, and 6. Unlike prime numbers, which are only divisible by 1 and themselves, composite numbers offer more possibilities for division.
1.3. Examples of Composite Numbers in Action
Some of the initial composite numbers include 4, 6, 8, 9, and 10. Take 4, for example. Its factors are 1, 2, and 4. Similarly, 6 has factors 1, 2, 3, and 6. These examples highlight how composite numbers have multiple factors, making them different from prime numbers.
2. Identifying Composite Numbers: How To Find Them
To determine if a number is composite, you need to find its factors. If a number has more than two factors, it is composite. This process often involves divisibility tests, which can quickly identify composite numbers.
2.1. Methods to Find Composite Numbers Easily
One effective method is the divisibility test. Check if the number is divisible by common factors such as 2, 3, 5, 7, 11, and 13. If the number is even, start with 2. If it ends in 0 or 5, check divisibility by 5. If it’s divisible by any of these numbers, it’s composite.
2.2. Using Divisibility Tests for Composite Numbers
Divisibility tests are essential for identifying composite numbers. For instance, 48 is divisible by 2, 3, 4, 6, 8, 12, 16, and 24, in addition to 1 and 48. This demonstrates that 48 has more than two factors, confirming it as a composite number.
2.3. Prime Factorization and Composite Numbers
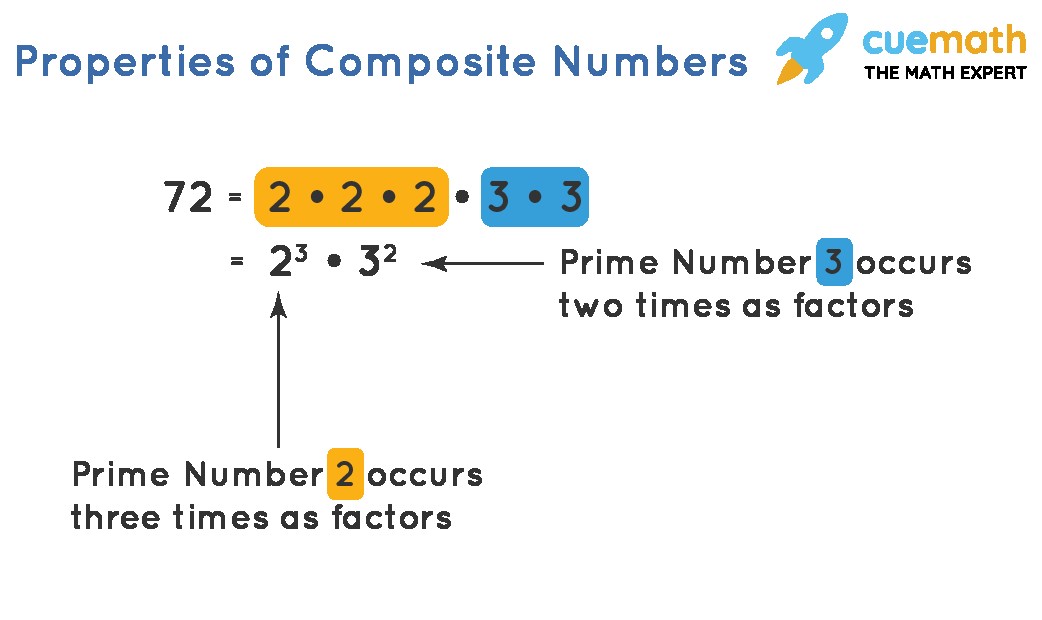
Prime factorization is another method to identify composite numbers. If a number can be expressed as a product of prime numbers, it is composite. For example, 12 = 2 x 2 x 3. Since 12 can be broken down into prime factors, it is a composite number.
3. Properties of Composite Numbers: Key Attributes
Composite numbers have distinct properties that set them apart from prime numbers. These properties are important in number theory and in understanding the structure of numbers.
3.1. Understanding Composite Number Properties
A fundamental property of composite numbers is that they can be divided evenly by numbers other than 1 and themselves. Additionally, every composite number can be expressed as a product of prime numbers. These factors may be prime or composite, but ultimately, they can be broken down into primes.
3.2. Prime Factors and Composite Numbers
Every composite number is composed of two or more prime numbers. This relationship is crucial in understanding the composition of numbers. For example, the composite number 20 can be expressed as 2 x 2 x 5, where 2 and 5 are prime factors.
3.3. Integer Multiplication and Composite Numbers
Composite numbers can be formed by multiplying two smaller positive integers. For example, 4 x 3 = 12, where 12 is a composite number. This multiplication property is a direct result of having more than two factors.
3.4. The First 10 Composite Numbers
The first 10 composite numbers are: 4, 6, 8, 9, 10, 12, 14, 15, 16, and 18. These numbers all share the characteristic of having more than two factors. Recognizing these initial composite numbers can help in understanding larger composite numbers.
4. Types of Composite Numbers: Odd and Even
Composite numbers can be classified into two main types: odd composite numbers and even composite numbers. Each type has its own unique characteristics and examples.
4.1. Defining Odd Composite Numbers
Odd composite numbers are odd numbers that have more than two factors. These numbers are not divisible by 2 and have multiple divisors other than 1 and themselves.
4.2. Examples of Odd Composite Numbers
Examples of odd composite numbers include 9, 15, 21, 25, and 27. For instance, 9 has factors 1, 3, and 9, while 15 has factors 1, 3, 5, and 15. These examples highlight that odd composite numbers always have at least one odd factor other than 1 and themselves.
4.3. Identifying Even Composite Numbers
Even composite numbers are even numbers that have more than two factors. These numbers are divisible by 2 and have multiple divisors.
4.4. Examples of Even Composite Numbers
Examples of even composite numbers include 4, 6, 8, 10, 12, 14, and 16. For example, 4 has factors 1, 2, and 4, while 6 has factors 1, 2, 3, and 6. These numbers are divisible by 2 and have additional factors, making them composite.
5. The Smallest Composite Number: An Introduction
The smallest composite number is 4. This number is the first positive integer that has more than two factors, making it a foundational concept in number theory.
5.1. Why 4 Is the Smallest Composite Number
Starting with 1, we know that 1 is neither prime nor composite because it has only one factor. The number 2 is prime because it has only two factors (1 and 2). Similarly, 3 is prime with factors 1 and 3. However, 4 has factors 1, 2, and 4, satisfying the criteria for a composite number.
5.2. Understanding Numbers Smaller than 4
Numbers smaller than 4 are either prime or neither prime nor composite. The number 1 has only one factor, and the numbers 2 and 3 are prime numbers because they have exactly two factors. This distinction clarifies why 4 is the smallest composite number.
5.3. Prime Numbers vs. Composite Numbers
Prime numbers have only two factors: 1 and themselves. Composite numbers have more than two factors. This distinction is crucial in understanding the fundamental building blocks of numbers. For example, 7 is a prime number with factors 1 and 7, whereas 8 is a composite number with factors 1, 2, 4, and 8.
6. Common Questions About Composite Numbers
6.1. What are Composite Numbers in Math?
Composite numbers are natural numbers that have more than two factors. They can be divided evenly by numbers other than 1 and themselves, making them “composed” of multiple factors. For instance, 12 is a composite number because it is divisible by 1, 2, 3, 4, 6, and 12.
6.2. How to Find Composite Numbers?
To find composite numbers, identify numbers with more than two factors. This can be done through divisibility tests or by finding the factors of the given number. If a number can be divided evenly by a number other than 1 and itself, it is composite.
6.3. Is 2 a Composite Number?
No, 2 is not a composite number. It is a prime number because it has exactly two factors: 1 and 2. Prime numbers are only divisible by 1 and themselves.
6.4. What are the Composite Numbers Between 1 and 100?
The composite numbers between 1 and 100 include: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, and 100.
6.5. What are Prime and Composite Numbers?
Prime numbers have only two factors (1 and themselves), while composite numbers have more than two factors. For example, 7 is a prime number with factors 1 and 7, whereas 8 is a composite number with factors 1, 2, 4, and 8.
6.6. What is an Odd Composite Number?
An odd composite number is an odd number that has more than two factors. Examples include 9, 15, 21, and 25. These numbers are not divisible by 2 and have multiple divisors.
6.7. What is the Smallest Composite Number?
The smallest composite number is 4 because it is the first number with more than two factors (1, 2, and 4).
6.8. What is the Difference Between a Prime and a Composite Number?
The primary difference is the number of factors. Prime numbers have exactly two factors, while composite numbers have more than two factors. This distinction is crucial in understanding the nature of numbers.
6.9. What are Consecutive Composite Numbers?
Consecutive composite numbers are composite numbers that follow each other without any prime numbers in between. Examples include 8, 9, and 10.
6.10. How many Composite Numbers are there from 1 to 100?
There are 74 composite numbers from 1 to 100. These numbers can be listed as: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, and 100.
6.11. What Composite Numbers are Between 6 and 11?
The composite numbers between 6 and 11 are 8, 9, and 10. These numbers have more than two factors.
6.12. Which of the Factors of 120 are Composite Numbers?
The factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120. The composite numbers among these factors are 4, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120.
6.13. What are the First Four Composite Numbers?
The first four composite numbers are 4, 6, 8, and 9.
6.14. Which is the Smallest Odd Composite Number?
The smallest odd composite number is 9.
6.15. Which is the First Composite Number?
The first composite number is 4.
6.16. What are the First Five Composite Numbers?
The first five composite numbers are 4, 6, 8, 9, and 10.
Unlock More Mathematical Knowledge
Want to explore more mathematical concepts and get instant answers? At WHAT.EDU.VN, we provide a free platform to ask any question and receive quick, accurate responses. Whether you’re a student, professional, or just curious, our expert resources are here to help.
Instant Answers, Free Consultations
Struggling with a tricky math problem or curious about a real-world application? Don’t waste time searching endlessly. Ask your questions on WHAT.EDU.VN and get immediate assistance. Our community of experts is ready to provide free consultations and detailed explanations.
Join Our Community
Connect with other learners, share your knowledge, and explore a wide range of topics. WHAT.EDU.VN is more than just a Q&A site; it’s a community where knowledge is shared and curiosity is encouraged.
Ready to Ask?
Don’t let your questions go unanswered. Visit WHAT.EDU.VN today and experience the ease of getting the information you need.
Call to Action
Ready to dive deeper into the world of numbers and unlock more mathematical knowledge? Ask your question now at WHAT.EDU.VN and get a free, quick answer. Don’t let confusion hold you back – our experts are here to help you understand even the most complex concepts. Join our community today and start your journey to mathematical mastery!
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn