Are you curious about what “congruent” truly means and how it applies in geometry? WHAT.EDU.VN provides a clear and comprehensive explanation. In essence, congruence signifies that two figures are exactly identical in shape and size. Keep reading to explore congruent figures, their properties, and how they differ from similar figures.
1. Congruent Meaning in Geometry
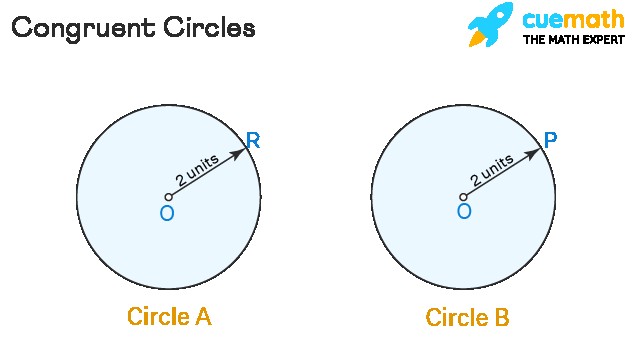
In geometry, “congruent” describes figures that are exactly the same in both shape and size. This means that if you were to overlay one congruent figure onto another, they would perfectly match. This remains true even if you rotate, flip, or turn the shapes. Imagine drawing two circles with the exact same radius. If you cut them out and place one on top of the other, they would perfectly overlap. This demonstrates that the two circles are congruent. The symbol used to denote congruence is “≅”. Therefore, if circle A is congruent to circle B, we can write it as Circle A ≅ Circle B.
Two circles with equal radius showing congruence
2. Understanding Congruent Figures
The defining characteristic of congruent figures is their ability to perfectly overlap when placed on top of each other. Congruence expresses the relationship between two such figures. In simpler terms, if you can superimpose one geometrical figure onto another, they are considered congruent. This principle applies to all geometric figures, including triangles, quadrilaterals, and other polygons. Beyond figures, line segments and angles can also be congruent if they have the same measure.
Various congruent shapes, including triangles and quadrilaterals
3. Congruent vs. Similar Figures: What’s the Difference?
While both terms relate to geometric figures, congruence and similarity have distinct meanings. Congruent figures are identical, meaning their corresponding sides are the same length, and their corresponding angles have the same measure. Similar figures, on the other hand, share the same shape, but their sizes can differ. This means their corresponding angles are equal, but their corresponding sides are proportional, not necessarily equal.
For example, consider two triangles. If they are congruent, all three sides and all three angles of one triangle will be exactly the same as the corresponding sides and angles of the other triangle. If they are similar, the angles will be the same, but one triangle might be a scaled-up or scaled-down version of the other.
Illustrating the difference between congruent and similar triangles
3.1. Delving Into Triangle Congruence
Two triangles are congruent if their corresponding sides are equal in length, their corresponding angles are equal in measure, and one triangle can be perfectly superimposed onto the other.
Two congruent triangles, Δ ABC and Δ PQR, demonstrating equal sides and angles
In the figure above, Δ ABC and Δ PQR are congruent triangles. This means that the corresponding angles and corresponding sides in both triangles are equal:
- Sides: AB = PQ, BC = QR, and AC = PR
- Angles: ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R
Therefore, we can write: Δ ABC ≅ Δ PQR.
The following are the congruence theorems or the triangle congruence criteria that help to prove the congruence of triangles:
- SSS (Side, Side, Side): If all three sides of one triangle are equal to the corresponding three sides of another triangle, then the two triangles are congruent.
- SAS (Side, Angle, Side): If two sides and the included angle (the angle between those two sides) of one triangle are equal to the corresponding two sides and included angle of another triangle, then the two triangles are congruent.
- ASA (Angle, Side, Angle): If two angles and the included side (the side between those two angles) of one triangle are equal to the corresponding two angles and included side of another triangle, then the two triangles are congruent.
- AAS (Angle, Angle, Side): If two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the two triangles are congruent.
- RHS (Right angle-Hypotenuse-Side): Applicable only to right-angled triangles. If the hypotenuse and one side of one right-angled triangle are equal to the hypotenuse and corresponding side of another right-angled triangle, then the two triangles are congruent. This is also known as the Hypotenuse Leg theorem.
4. Real-World Congruent Examples
4.1. Example 1: Identifying Corresponding Angles in Congruent Quadrilaterals
The two quadrilaterals shown below are congruent. Which angle in quadrilateral PQRS corresponds to ∠WXY in quadrilateral WXYZ?
Solution:
To identify the corresponding parts, we need to compare the markings on the angles. ∠WXY is marked with four arcs in quadrilateral WXYZ. ∠QRS is also marked with four arcs in quadrilateral PQRS. This indicates that they are equal.
Therefore, ∠WXY corresponds to ∠QRS.
4.2. Example 2: Finding Congruent Squares
Emma has four squares with the following side lengths:
- Square A: side = 5 inches
- Square B: side = 7 inches
- Square C: side = 5 inches
- Square D: side = 8 inches
She wants to find two squares that can be placed exactly on top of each other. Can you help her choose the congruent squares?
Solution:
Squares are congruent when their side lengths are identical. By comparing the side lengths, we can see that Square A and Square C both have sides of 5 inches.
Therefore, Emma can choose Square A and Square C because they are congruent and can be placed exactly one over the other.
5. Congruent: Frequently Asked Questions (FAQs)
5.1. What Exactly Are Congruent Figures?
Congruent figures are geometrical figures with matching sides and angles. Think of them as identical twins; they perfectly overlap even when rotated or flipped, emphasizing their exact similarity in both shape and size.
5.2. How Can You Prove that Two Triangles Are Congruent?
Proving triangle congruence involves demonstrating that their corresponding sides and angles are equal. You can use congruence theorems like SSS, SAS, ASA, AAS, or RHS to systematically prove that two triangles are congruent.
5.3. What Are the Key Properties of Congruence?
Congruence exhibits three fundamental properties applicable to lines, angles, and figures:
- Reflexive Property: Any geometric figure is congruent to itself (e.g., ∠A ≅ ∠A).
- Symmetric Property: If one figure is congruent to another, the reverse is also true (if ∠A ≅ ∠B, then ∠B ≅ ∠A).
- Transitive Property: If one figure is congruent to a second, and the second is congruent to a third, then the first is also congruent to the third.
5.4. Which Shape Has All Congruent Sides and Angles?
A square stands out as the shape with four congruent sides and four right angles. This unique combination defines its symmetrical and balanced structure.
5.5. What Are the Five Key Triangle Congruence Criteria?
The five triangle congruence criteria are:
- SSS (Side-Side-Side): All three sides are equal.
- SAS (Side-Angle-Side): Two sides and the included angle are equal.
- ASA (Angle-Side-Angle): Two angles and the included side are equal.
- AAS (Angle-Angle-Side): Two angles and a non-included side are equal.
- RHS (Right-Hypotenuse-Side): The hypotenuse and one side of right triangles are equal.
5.6. Are Vertical Angles Always Congruent?
Yes, vertical angles are always congruent. This principle stems from the vertical angles theorem, which states that when two straight lines intersect, the angles opposite each other are equal.
5.7. What’s Another Word for Congruent?
Another word for congruent is identical. Congruent shapes are exactly the same in shape and size and can be perfectly superimposed on one another.
5.8. What Makes Angles Congruent?
Angles are deemed congruent when their measurements, whether in degrees or radians, are precisely the same. If ∠A = ∠B, these angles are congruent.
Do you still have questions about congruence or any other topic? Don’t hesitate to ask! At WHAT.EDU.VN, we provide a free platform to ask any question and receive prompt, accurate answers from knowledgeable individuals. We understand the frustration of searching for reliable information, the uncertainty of who to ask, and the worry of consultation costs.
Unlock a World of Knowledge at WHAT.EDU.VN
At WHAT.EDU.VN, we’re committed to providing you with:
- A Free Platform: Ask any question, no matter how simple or complex, without any cost.
- Prompt and Accurate Answers: Receive timely and reliable responses to your queries.
- Easy-to-Understand Information: We break down complex topics into easily digestible explanations.
- Community Support: Connect with others to exchange knowledge and gain diverse perspectives.
- Free Consultation: Get guidance on straightforward issues without incurring any fees.
Ready to Get Your Questions Answered?
Visit WHAT.EDU.VN today and experience the ease and convenience of our free question-and-answer platform. No more struggling to find answers – we’re here to help!
Contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Let what.edu.vn be your go-to resource for all your questions!