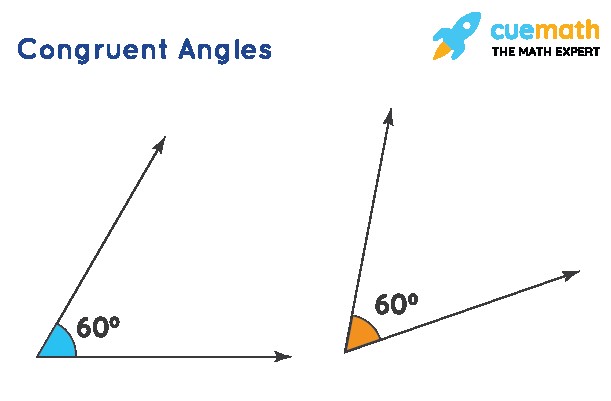
Congruent angles are angles that possess the same measure, a concept thoroughly explained by WHAT.EDU.VN, making complex geometric ideas understandable. If you’re seeking clarity on angle congruence and its applications, keep reading to discover how these angles behave and where they appear in geometric figures, plus explore the theorems that govern them and how to construct them accurately, enhancing your grasp of geometry. Dive in to explore supplementary angles, complementary angles, and vertical angles.
1. Understanding Congruent Angles
In geometry, congruent angles are defined as angles that have the exact same measure; in essence, they are equal angles. This equality is crucial in various geometric proofs and constructions. The symbol “≅” is used to denote congruence. For instance, if angle A is congruent to angle X, it is written as ∠A ≅ ∠X. These angles, having identical measures, can perfectly overlap each other. This concept is fundamental to understanding more complex geometric relationships, offering a clear and simple criterion for determining angle equivalence.
Congruent Angles in Real Life:
Congruent angles aren’t just confined to textbooks; they appear in numerous real-world scenarios, from the design of buildings to the creation of patterns. The precision required in these fields often relies on the accurate application of angle congruence.
2. Key Theorems Involving Congruent Angles
Several theorems rely on the concept of congruent angles, providing a framework for geometric proofs and problem-solving. These theorems help to establish relationships between angles and lines, which are crucial in geometry:
- Vertical Angles Theorem
- Corresponding Angles Theorem
- Alternate Angles Theorem
- Congruent Supplements Theorem
- Congruent Complements Theorem
2.1. Vertical Angles Theorem
This theorem states that vertical angles are always congruent. Vertical angles are formed when two lines intersect.
Statement: Vertical angles are congruent.
Proof:
This proof relies on the property of straight angles, which states that angles on a straight line add up to 180°.
| Statement | Reason |
|---|---|
| ∠1 + ∠2 = 180° | Linear Pair |
| ∠1 + ∠4 = 180° | Linear Pair |
| ∴ ∠1 + ∠2 = ∠1 + ∠4 | Equating above |
| ∴ ∠2 = ∠4 | Subtraction |
| Also, ∠1 = ∠3 | Similar proof |
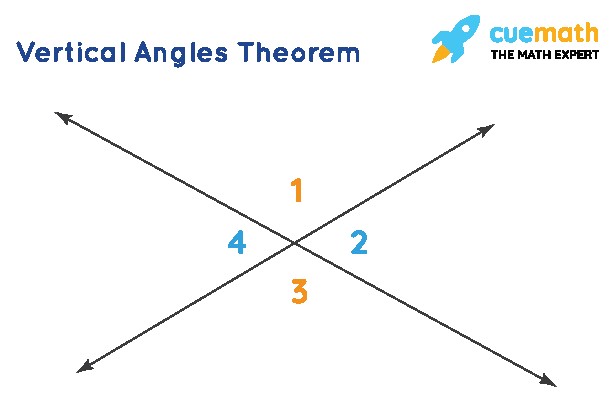

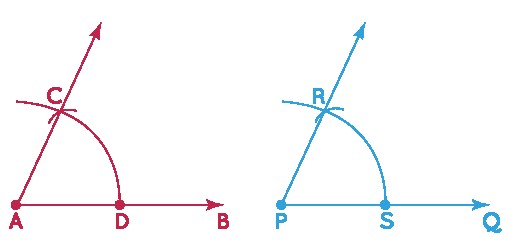
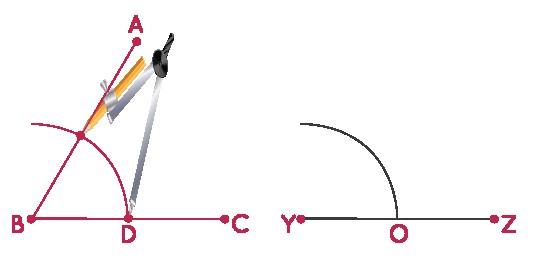
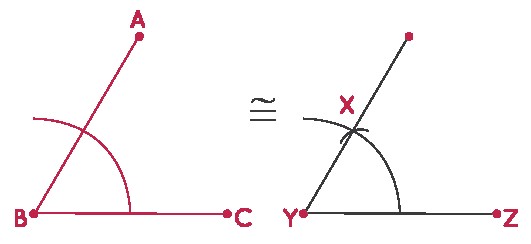
Conclusion: Vertical angles are always congruent.
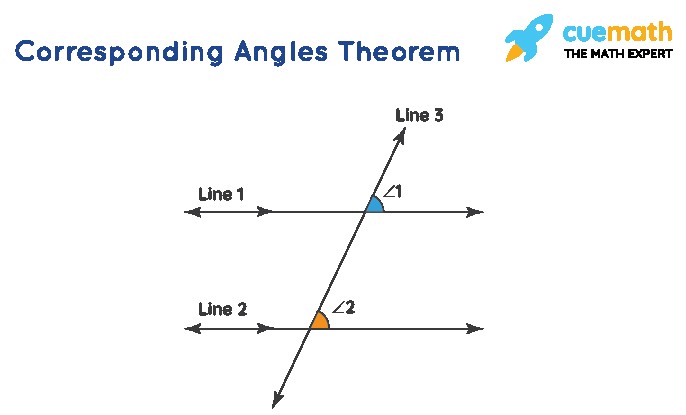
2.2. Corresponding Angles Theorem
When a transversal intersects two parallel lines, the angles in the same relative position at each intersection are corresponding angles, and they are congruent.
Statement: If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
In the figure, ∠1 = ∠2.
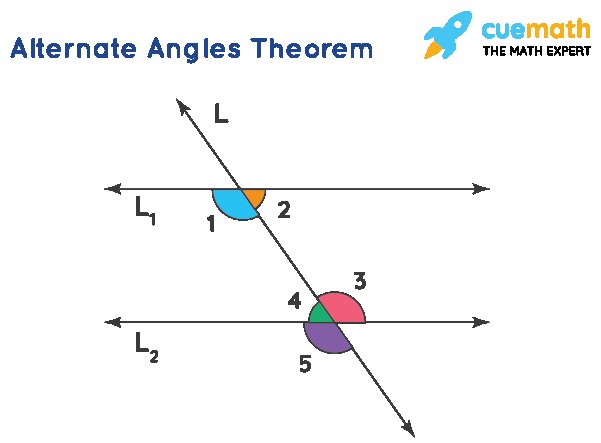
2.3. Alternate Angles Theorem
When a transversal intersects two parallel lines, the alternate interior angles are congruent, and the alternate exterior angles are congruent.
Statement: If two parallel lines are cut by a transversal, then the alternate angles are congruent.
From the figure:
- ∠1 = ∠5 (corresponding angles)
- ∠3 = ∠5 (vertical angles)
Thus, ∠1 = ∠3.
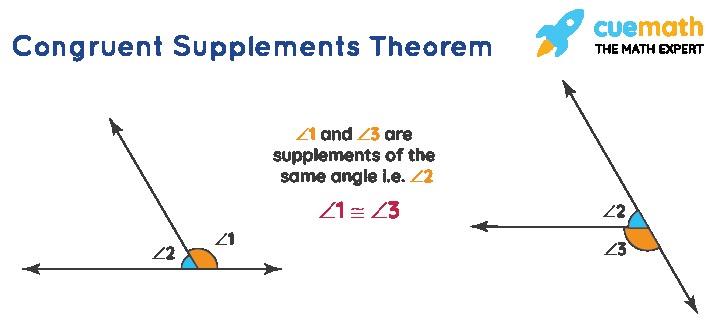
2.4. Congruent Supplements Theorem
Angles that are supplementary to the same angle are congruent. Supplementary angles add up to 180°.
Statement: Angles supplementary to the same angle are congruent.
Proof:
- ∠1 + ∠2 = 180° (Linear pair)
- ∠2 + ∠3 = 180° (Linear pair)
Therefore, ∠1 = ∠3.
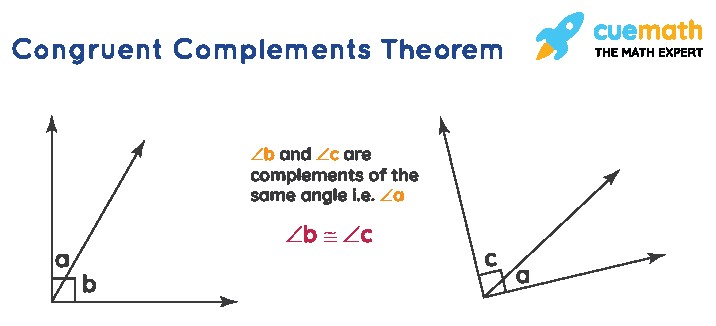
2.5. Congruent Complements Theorem
Angles that are complementary to the same angle are congruent. Complementary angles add up to 90°.
Statement: Angles complementary to the same angle are congruent.
Proof:
- ∠a + ∠b = 90°
- ∠a + ∠c = 90°
Therefore, ∠b ≅ ∠c.
3. Constructing Congruent Angles
Understanding how to construct congruent angles is essential in geometry. There are two main scenarios:
- Constructing two congruent angles of any measurement.
- Constructing an angle congruent to a given angle.
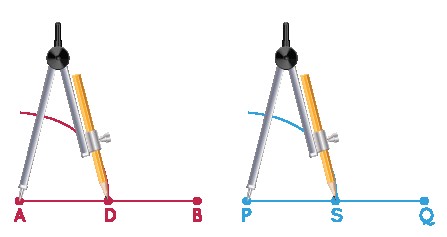
3.1. Constructing Two Congruent Angles with any Measurement
Here are the steps to construct two congruent angles:
Step 1: Draw two horizontal lines of any suitable length using a ruler.
Step 2: Set a compass to any arc length. Place the compass tip at one endpoint of each line and draw an arc.
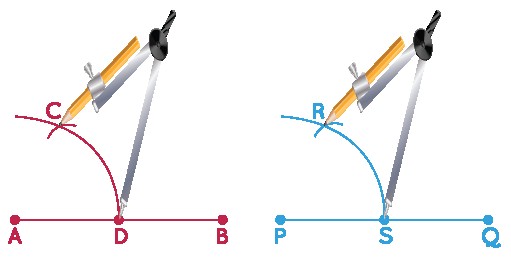
Step 3: Adjust the compass to another arc length. Place the compass tip at the intersection point on each line and draw another arc that intersects the first arc.
Step 4: Draw lines from the endpoints through the intersection points of the arcs.
The resulting angles, ∠CAB and ∠RPQ, are congruent.
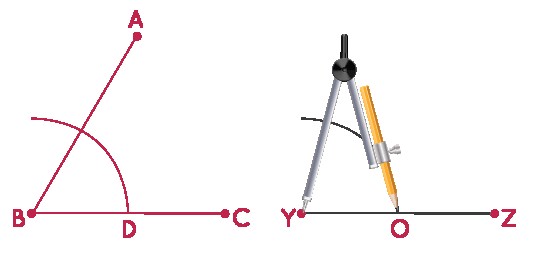
3.2. Constructing a Congruent Angle to the Given Angle
If you have a specific angle and need to construct a congruent angle, follow these steps:
Suppose you have ∠ABC and you want to construct a congruent angle.
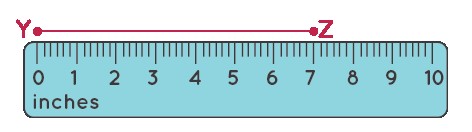
Step 1: Draw a horizontal line YZ.
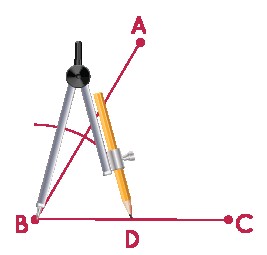
Step 2: Place the compass tip at point B and draw an arc intersecting both sides of the angle, labeling the intersection with BC as D.
Step 3: Keep the same compass width, place the compass tip at point Y, and draw an arc intersecting line YZ at point O.
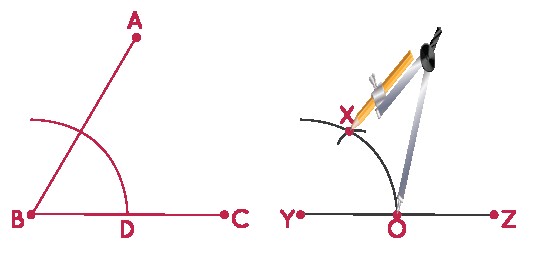
Step 4: Measure the distance between point D and the intersection of the arc on segment AB with the compass.
Step 5: With the same compass width, place the compass tip at point O and mark a cut at the arc drawn in step 3, labeling that point X.
Step 6: Draw a line joining points X and Y.
Now, ∠ABC ≅ ∠XYZ.
4. Solved Examples of Congruent Angles
Understanding congruent angles becomes easier with practical examples. These examples illustrate how congruent angle theorems are applied to solve geometric problems.
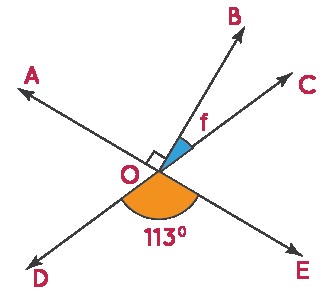
Example 1: Find the measurement of angle f.
Solution:
∠DOE and ∠AOC are vertical angles and therefore congruent.
∠DOE = ∠AOC
113° = 90° + f
f = 113° – 90°
f = 23°
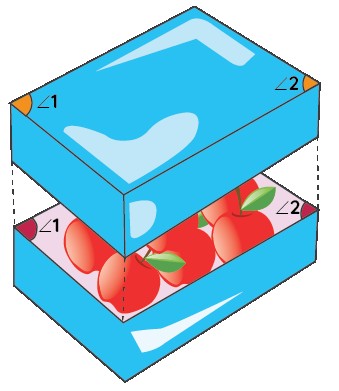
Example 2: Consider a parallelogram-shaped lunchbox. The best match of angles on the lid helps to close the box. Why?
Solution:
The best fit of congruent angles ensures the lid closes properly. Corresponding angles are congruent, ensuring every corner of the lid matches the box.
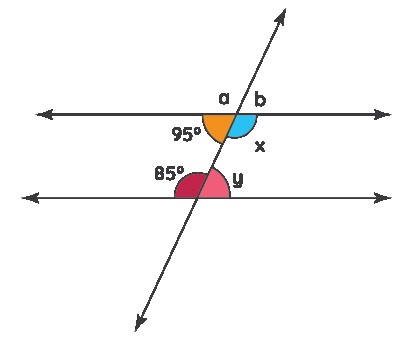
Example 3: In the figure, two parallel lines are intersected by a transversal. Find the measure of ∠x and ∠y.
Solution:
According to the alternate angles theorem, ∠x and the 85° angle are alternate congruent angles, so ∠x = 85°. Similarly, ∠y and the 95° angle are congruent alternate angles, so ∠y = 95°.
5. Congruent Angles: Tips and Tricks
- Congruent angles are equal angles.
- Vertical angles are congruent.
- Alternate and corresponding angles formed by a transversal intersecting parallel lines are congruent.
- Angles must have the same measurement to be congruent.
6. Practice Questions on Congruent Angles
Test your understanding with these practice questions:
- Two angles are said to be congruent if they measure _____.
- If two triangles are similar, their angles are:
- If two parallel lines are cut by a transversal line, then the corresponding angles are:
- If two angles A and B are congruent angles and the measure of angle A is 45 degrees, then the measure of angle B is:
- If two parallel lines are cut by a transversal line, then the alternate interior angles are:
7. FAQs About Congruent Angles
7.1. What does Congruent Angles mean?
Congruent angles are angles with equal measurements that can be placed perfectly on top of each other.
7.2. What are the Conditions Required for Congruent Angles?
Angles must have the same measurement to be congruent.
7.3. Do Congruent Angles Add up to 180?
Not generally. For angles to add up to 180, they must be supplementary. Only right angles are both congruent and supplementary.
7.4. Are Right Angles Congruent?
Yes, all right angles are congruent as they each measure 90°.
7.5. What are Congruent Angles in Parallel Lines?
Corresponding angles, vertical angles, alternate interior angles, and alternate exterior angles are congruent when parallel lines are intersected by a transversal.
7.6. How do we Know if Angles are Congruent?
Check if their measurements are the same using a protractor.
7.7. Are Congruent Angles Equal?
Yes, congruent angles are equal angles.
7.8. How to Find Congruent Angles?
Identify angles with the same measurement.
7.9. What Type of Angles are always Congruent?
Vertically opposite angles, alternate angles, and corresponding angles on parallel lines and transversals are always congruent. Additionally, angles supplementary to the same angle and angles complementary to the same angle are congruent.
Navigating the world of geometry can be challenging, but WHAT.EDU.VN is here to help. If you have more questions or need further clarification on any topic, don’t hesitate to ask. Our platform is designed to provide you with quick, accurate, and free answers to all your queries. Visit WHAT.EDU.VN today and experience the ease of learning with expert assistance.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn
