Decimals are all around us, from prices in stores to measurements in recipes. At WHAT.EDU.VN, we’re committed to providing clear and concise answers to your questions, ensuring you grasp the fundamentals of mathematics. Let’s explore what a decimal is, how it works, and why it’s an essential part of everyday life, focusing on decimal fractions, place value, and decimal numbers to enhance your understanding.
1. What Is A Decimal Number?
A decimal number is a way of representing numbers that include both a whole number part and a fractional part. The two parts are separated by a decimal point. In essence, it’s a number written in base-10 notation. Decimal numbers are crucial for representing values that are not whole numbers, providing a more precise way to express quantities.
Consider the number 3.14. Here, 3 is the whole number part, and .14 is the fractional part, representing fourteen-hundredths. This representation is more precise than using whole numbers alone.
2. What Are the Key Components of a Decimal?
Understanding the structure of a decimal number is crucial for performing operations and interpreting values correctly. A decimal consists of several key components.
- Whole Number Part: This is the integer to the left of the decimal point. It represents the complete units.
- Decimal Point: This is the dot that separates the whole number part from the fractional part.
- Fractional Part: This is the part to the right of the decimal point. It represents a fraction of a whole unit. Each digit in the fractional part has a specific place value.
For example, in the number 12.45, “12” is the whole number part, “.” is the decimal point, and “45” is the fractional part. The “4” represents four-tenths, and the “5” represents five-hundredths.
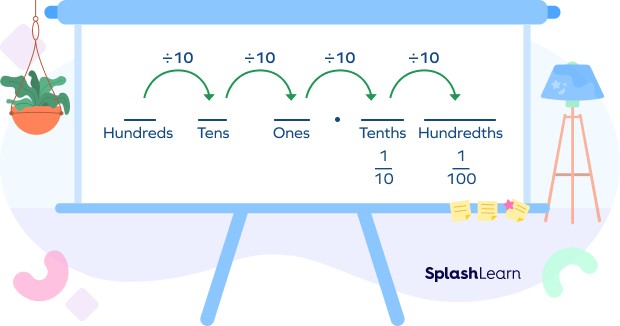
3. What is Decimal Place Value?
Decimal place value refers to the value of each digit based on its position relative to the decimal point. Each position to the right of the decimal point represents a fraction with a denominator of 10 raised to a power.
Here’s a breakdown:
- Tenths: The first digit to the right of the decimal point represents tenths (1/10 or 0.1).
- Hundredths: The second digit represents hundredths (1/100 or 0.01).
- Thousandths: The third digit represents thousandths (1/1000 or 0.001).
- Ten-Thousandths: The fourth digit represents ten-thousandths (1/10000 or 0.0001), and so on.
Understanding place value is crucial for performing arithmetic operations, comparing decimal numbers, and converting decimals to fractions.
4. How Do You Read Decimal Numbers?
Reading decimal numbers correctly involves understanding both the whole number part and the fractional part.
Here’s a step-by-step guide:
- Read the whole number part as you normally would.
- Say “point” at the decimal point.
- Read the digits to the right of the decimal point individually.
For example:
- 3.14 is read as “three point one four.”
- 15.025 is read as “fifteen point zero two five.”
- 0.75 is read as “zero point seven five.”
Alternatively, you can read the fractional part by stating its place value:
- 3.14 can be read as “three and fourteen hundredths.”
- 15.025 can be read as “fifteen and twenty-five thousandths.”
5. What Are Different Types of Decimals?
Decimals can be classified into several types based on their properties:
- Terminating Decimals: These decimals have a finite number of digits after the decimal point. For example, 0.5, 0.75, and 0.125 are terminating decimals.
- Repeating Decimals: These decimals have a pattern of digits that repeats indefinitely. For example, 0.333…, 0.142857142857…, and 1.666… are repeating decimals. The repeating part is often indicated with a bar over the repeating digits (e.g., 0.3̄, 1.6̄).
- Non-Terminating, Non-Repeating Decimals: These decimals have an infinite number of digits after the decimal point, and there is no repeating pattern. These numbers are irrational numbers. A classic example is pi (π ≈ 3.1415926535…).
6. How Do You Convert Fractions to Decimals?
Converting fractions to decimals is a fundamental skill in mathematics. It involves dividing the numerator of the fraction by its denominator.
Steps to Convert a Fraction to a Decimal:
- Divide: Divide the numerator (the top number) by the denominator (the bottom number).
- Decimal Point: If the division results in a remainder, add a decimal point to the dividend (the numerator) and continue dividing by adding zeros as needed.
- Result: The result is the decimal equivalent of the fraction.
Examples:
- 1/2: Divide 1 by 2. The result is 0.5.
- 3/4: Divide 3 by 4. The result is 0.75.
- 1/3: Divide 1 by 3. The result is 0.333…, which is a repeating decimal.
7. How Do You Convert Decimals to Fractions?
Converting decimals to fractions involves expressing the decimal as a ratio of two integers.
Steps to Convert a Decimal to a Fraction:
- Write as a Fraction: Write the decimal as a fraction with a denominator of 1, then remove decimal by multiplying both numerator and denominator by 10.
- Count Decimal Places: Count the number of digits after the decimal point. This number determines the power of 10 you’ll use as the denominator.
- Simplify: Simplify the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
Examples:
- 0.5: Write 0.5 as 5/10. Simplify to 1/2.
- 0.75: Write 0.75 as 75/100. Simplify to 3/4.
- 0.125: Write 0.125 as 125/1000. Simplify to 1/8.
8. What Are the Basic Operations with Decimals?
Performing basic arithmetic operations with decimals requires careful alignment of decimal points to ensure accurate results.
Addition:
- Align: Align the decimal points of the numbers vertically.
- Add: Add the numbers as you would with whole numbers, starting from the rightmost column.
- Carry Over: Carry over values if the sum in a column is greater than 9.
- Place Decimal Point: Place the decimal point in the sum directly below the decimal points in the numbers being added.
Subtraction:
- Align: Align the decimal points of the numbers vertically.
- Subtract: Subtract the numbers as you would with whole numbers, starting from the rightmost column.
- Borrow: Borrow from the next column if necessary.
- Place Decimal Point: Place the decimal point in the difference directly below the decimal points in the numbers being subtracted.
Multiplication:
- Multiply: Multiply the numbers as you would with whole numbers, ignoring the decimal points.
- Count Decimal Places: Count the total number of decimal places in the numbers being multiplied.
- Place Decimal Point: Place the decimal point in the product so that it has the same number of decimal places as the total counted in step 2.
Division:
- Set Up: Set up the division problem with the dividend (the number being divided) inside the division symbol and the divisor (the number you are dividing by) outside.
- Move Decimal Point: If the divisor is a decimal, move the decimal point to the right until it becomes a whole number. Move the decimal point in the dividend the same number of places.
- Divide: Perform the division as you would with whole numbers.
- Place Decimal Point: Place the decimal point in the quotient (the answer) directly above the decimal point in the dividend.
9. What Are Real-World Applications of Decimals?
Decimals are used extensively in various real-world applications, providing the precision needed for many everyday tasks.
- Finance: Calculating interest rates, taxes, and currency exchange rates.
- Measurement: Measuring length, weight, volume, and temperature in various units.
- Science: Performing calculations in physics, chemistry, and engineering.
- Cooking: Adjusting recipe measurements for different serving sizes.
- Sports: Calculating averages, statistics, and performance metrics.
10. How Are Decimals Used in Measurement?
In measurement, decimals provide a way to express quantities with greater precision than whole numbers alone.
Here are some examples:
- Length: A piece of wood might be 2.5 meters long, indicating it is longer than 2 meters but not quite 3 meters.
- Weight: A bag of flour might weigh 1.75 kilograms, showing a weight between 1 and 2 kilograms.
- Temperature: The temperature might be 23.6 degrees Celsius, providing a more precise reading than 23 or 24 degrees alone.
Decimals are particularly useful in fields where accuracy is crucial, such as engineering, construction, and manufacturing.
11. Decimals vs. Fractions: Which Should You Use?
Decimals and fractions are both ways to represent parts of a whole, but they have different strengths and are used in different contexts.
- Decimals: Decimals are often preferred when precision is important, and calculations need to be performed quickly. They are commonly used in measurements, finance, and scientific calculations.
- Fractions: Fractions are useful when dealing with exact values and proportions. They are often used in cooking, construction, and situations where understanding ratios is important.
The choice between decimals and fractions often depends on the specific application and the level of precision required.
12. What are Repeating Decimals and How Do You Handle Them?
Repeating decimals, also known as recurring decimals, are decimal numbers that have a repeating sequence of digits after the decimal point. These decimals can be represented as fractions, and understanding how to handle them is essential for accurate calculations.
Identifying Repeating Decimals
Repeating decimals have a pattern of digits that repeats indefinitely. This pattern is often indicated with a bar over the repeating digits. For example, 0.3̄ represents 0.3333…, and 1.6̄ represents 1.6666….
Converting Repeating Decimals to Fractions
To convert a repeating decimal to a fraction, you can use algebraic methods:
- Set up an equation: Let x equal the repeating decimal.
- Multiply by a power of 10: Multiply both sides of the equation by a power of 10 that moves one repeating block to the left of the decimal point.
- Subtract the original equation: Subtract the original equation from the new equation to eliminate the repeating part.
- Solve for x: Solve the resulting equation for x, which will give you the fraction equivalent of the repeating decimal.
For example, let’s convert 0.3̄ to a fraction:
- Let x = 0.3333…
- Multiply by 10: 10x = 3.3333…
- Subtract the original equation: 10x – x = 3.3333… – 0.3333…
- Simplify: 9x = 3
- Solve for x: x = 3/9 = 1/3
Therefore, 0.3̄ is equal to 1/3.
Examples of Converting Repeating Decimals
- Convert 0.6̄ to a fraction:
- Let x = 0.6666…
- Multiply by 10: 10x = 6.6666…
- Subtract the original equation: 10x – x = 6.6666… – 0.6666…
- Simplify: 9x = 6
- Solve for x: x = 6/9 = 2/3
- Convert 0.14̄ to a fraction:
- Let x = 0.141414…
- Multiply by 100: 100x = 14.141414…
- Subtract the original equation: 100x – x = 14.141414… – 0.141414…
- Simplify: 99x = 14
- Solve for x: x = 14/99
13. How to Round Decimals
Rounding decimals is a method used to simplify numbers by reducing the number of digits to the right of the decimal point. This is often done to make numbers easier to work with or to present them in a more concise form.
Steps to Round Decimals
- Identify the digit to be rounded: Determine which decimal place you want to round to (e.g., tenths, hundredths, thousandths). The digit in that place is the one you will round.
- Look at the next digit to the right: This digit is the “test digit.” It will determine whether you round up or down.
- Rounding Rules:
- If the test digit is 0, 1, 2, 3, or 4, round down. This means the digit being rounded stays the same.
- If the test digit is 5, 6, 7, 8, or 9, round up. This means the digit being rounded increases by 1. If the digit being rounded is a 9, it becomes a 0, and the digit to the left increases by 1 (similar to carrying over in addition).
- Drop the remaining digits: Remove all digits to the right of the rounded digit.
Examples of Rounding Decimals
- Round 3.14159 to the nearest hundredth:
- The hundredths digit is 4.
- The test digit is 1 (to the right of 4).
- Since 1 is less than 5, round down.
- Result: 3.14
- Round 2.789 to the nearest tenth:
- The tenths digit is 7.
- The test digit is 8 (to the right of 7).
- Since 8 is greater than or equal to 5, round up.
- Result: 2.8
- Round 0.996 to the nearest hundredth:
- The hundredths digit is 9.
- The test digit is 6 (to the right of 9).
- Since 6 is greater than or equal to 5, round up.
- The 9 in the hundredths place becomes a 0, and we carry over to the tenths place, making it 1.00.
- Result: 1.00
Common Scenarios for Rounding Decimals
- Money: When dealing with money, rounding to the nearest cent (hundredth) is common. For example, $3.456 would be rounded to $3.46.
- Measurement: In scientific and engineering applications, rounding is often used to present measurements with an appropriate level of precision. For example, if a measurement is 2.3456 meters, it might be rounded to 2.35 meters if the measuring tool is only accurate to the nearest hundredth of a meter.
14. Estimating with Decimals
Estimating with decimals involves approximating decimal numbers to whole numbers or simpler decimals to make calculations easier. This is a useful skill for quickly checking the reasonableness of answers or for making quick decisions when precise calculations are not necessary.
Methods for Estimating with Decimals
- Rounding to the Nearest Whole Number:
- Round each decimal number to the nearest whole number.
- Perform the calculation with the rounded whole numbers.
- Example:
- Estimate 3.7 + 8.2:
- Round 3.7 to 4.
- Round 8.2 to 8.
- Estimate: 4 + 8 = 12
- Using Compatible Numbers:
- Adjust the decimal numbers to compatible numbers that are easy to work with mentally.
- Perform the calculation with the adjusted numbers.
- Example:
- Estimate 6.8 x 4.1:
- Adjust 6.8 to 7.
- Adjust 4.1 to 4.
- Estimate: 7 x 4 = 28
- Front-End Estimation:
- Focus on the whole number part of the decimal and ignore the digits after the decimal point.
- Perform the calculation with the whole numbers.
- Example:
- Estimate 15.6 – 7.2:
- Use the whole numbers: 15 – 7 = 8
Examples of Estimating with Decimals
- Addition:
- Estimate the sum of 12.3 + 9.8 + 5.4:
- Round to the nearest whole number: 12 + 10 + 5 = 27
- Estimated sum: 27
- Subtraction:
- Estimate the difference of 25.7 – 11.4:
- Round to the nearest whole number: 26 – 11 = 15
- Estimated difference: 15
- Multiplication:
- Estimate the product of 4.6 x 7.9:
- Round to the nearest whole number: 5 x 8 = 40
- Estimated product: 40
- Division:
- Estimate the quotient of 47.8 ÷ 5.2:
- Round to the nearest whole number: 48 ÷ 5 ≈ 10 (since 5 x 10 = 50, which is close to 48)
- Estimated quotient: 10
15. Solving Word Problems with Decimals
Solving word problems with decimals involves applying decimal operations to real-world scenarios. Here are some tips for approaching these problems:
- Read Carefully: Understand the problem and identify what you need to find.
- Identify Key Information: Look for numbers (including decimals) and keywords that indicate which operations to use (addition, subtraction, multiplication, division).
- Set Up the Equation: Write an equation that represents the problem.
- Solve the Equation: Perform the necessary operations with the decimals.
- Check Your Answer: Make sure your answer is reasonable and makes sense in the context of the problem.
Examples of Solving Word Problems with Decimals
- Problem: A store sells apples for $1.75 per pound. If you buy 2.5 pounds of apples, how much will you pay?
- Equation: Total cost = price per pound × number of pounds
- Calculation: Total cost = $1.75 × 2.5 = $4.375
- Answer: You will pay $4.38 (rounded to the nearest cent).
- Problem: John ran 10.5 kilometers in 1.5 hours. What was his average speed in kilometers per hour?
- Equation: Average speed = total distance ÷ total time
- Calculation: Average speed = 10.5 km ÷ 1.5 hours = 7 km/hour
- Answer: John’s average speed was 7 kilometers per hour.
- Problem: A recipe calls for 0.75 cups of sugar. If you want to make half of the recipe, how much sugar do you need?
- Equation: Amount of sugar needed = original amount × 0.5
- Calculation: Amount of sugar needed = 0.75 cups × 0.5 = 0.375 cups
- Answer: You need 0.375 cups of sugar.
- Problem: A store is selling a shirt for $25.50 and is offering a 20% discount. What is the sale price of the shirt?
- Calculate the discount amount: Discount = original price × discount rate
- Discount = $25.50 × 0.20 = $5.10
- Calculate the sale price: Sale price = original price – discount
- Sale price = $25.50 – $5.10 = $20.40
- Answer: The sale price of the shirt is $20.40.
16. Common Mistakes to Avoid When Working with Decimals
Working with decimals can sometimes be tricky, and it’s easy to make mistakes. Here are some common errors to watch out for:
- Misaligning Decimal Points:
- Mistake: Not aligning decimal points when adding or subtracting.
- Correct Approach: Always align the decimal points vertically to ensure you are adding or subtracting the correct place values.
- Ignoring Place Value:
- Mistake: Not understanding the value of each digit after the decimal point.
- Correct Approach: Remember that each position to the right of the decimal point represents a fraction with a denominator of 10 raised to a power (tenths, hundredths, thousandths, etc.).
- Incorrectly Multiplying Decimals:
- Mistake: Forgetting to count the total number of decimal places in the factors when placing the decimal point in the product.
- Correct Approach: Count the decimal places in each factor and make sure the product has the same number of decimal places.
- Incorrectly Dividing Decimals:
- Mistake: Not moving the decimal point correctly in the divisor and dividend when dividing by a decimal.
- Correct Approach: Move the decimal point in the divisor to make it a whole number, and move the decimal point in the dividend the same number of places.
- Rounding Errors:
- Mistake: Rounding too early in a calculation, which can lead to inaccurate results.
- Correct Approach: Perform all calculations before rounding to the final answer.
- Misinterpreting Word Problems:
- Mistake: Not carefully reading and understanding the word problem, leading to the wrong operation or setup.
- Correct Approach: Read the problem carefully, identify key information, and set up the equation correctly.
- Forgetting to Simplify Fractions:
- Mistake: Converting a decimal to a fraction but not simplifying it to its lowest terms.
- Correct Approach: Always simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (GCD).
17. Practice Problems to Improve Decimal Skills
Practice is essential for mastering decimal skills. Here are some practice problems to help you improve:
Addition and Subtraction
- Calculate the sum: 4.56 + 8.29
- Find the difference: 15.75 – 6.32
- Solve: 23.8 + 9.15 – 12.6
Multiplication and Division
- Multiply: 3.25 × 2.4
- Divide: 18.5 ÷ 5
- Solve: 7.6 × 1.5 ÷ 0.2
Conversion
- Convert the fraction 3/8 to a decimal.
- Convert the decimal 0.625 to a fraction.
- Convert the repeating decimal 0.4̄ to a fraction.
Word Problems
- A store sells bananas for $0.65 per pound. If you buy 3.2 pounds of bananas, how much will you pay?
- John ran 8.75 kilometers in 1.25 hours. What was his average speed in kilometers per hour?
- A recipe calls for 0.6 cups of flour. If you want to make 1.5 times the recipe, how much flour do you need?
Estimation
- Estimate the sum: 7.8 + 11.2 + 4.9
- Estimate the difference: 31.5 – 16.3
- Estimate the product: 5.2 × 9.7
Answers to Practice Problems
Addition and Subtraction
- 12.85
- 9.43
- 20.35
Multiplication and Division
- 7.8
- 3.7
- 57
Conversion
- 0.375
- 5/8
- 4/9
Word Problems
- $2.08
- 7 km/hour
- 0.9 cups
Estimation
- 24
- 16
- 50
18. Advanced Topics Related to Decimals
Once you have a solid understanding of the basics of decimals, you can explore more advanced topics:
Scientific Notation
Scientific notation is a way of expressing very large or very small numbers using powers of 10. For example, the number 3,000,000 can be written as 3 × 10^6, and the number 0.000005 can be written as 5 × 10^-6. Scientific notation is commonly used in science and engineering to simplify calculations and express numbers in a concise format.
Significant Figures
Significant figures are the digits in a number that carry meaningful information about its precision. When performing calculations with measured values, it’s important to maintain the correct number of significant figures to avoid overstating the accuracy of the result.
Decimal Representation in Different Number Systems
While we commonly use base-10 (decimal) numbers, other number systems exist, such as binary (base-2), octal (base-8), and hexadecimal (base-16). Understanding how decimals are represented in these different number systems can be useful in computer science and digital electronics.
19. Tips for Teaching Decimals to Students
Teaching decimals to students can be challenging, but there are several strategies that can make the process easier and more effective:
- Start with Concrete Examples: Use real-world examples, such as money and measurement, to introduce the concept of decimals.
- Use Visual Aids: Use visual aids, such as place value charts and number lines, to help students understand the value of each digit in a decimal number.
- Hands-On Activities: Engage students in hands-on activities, such as using base-10 blocks to represent decimals and fractions.
- Relate to Fractions: Emphasize the connection between decimals and fractions, and show how to convert between the two.
- Provide Plenty of Practice: Give students plenty of opportunities to practice working with decimals through worksheets, games, and real-world problems.
- Address Common Misconceptions: Be aware of common misconceptions, such as misaligning decimal points or misunderstanding place value, and address them directly.
- Use Technology: Use technology, such as interactive simulations and online calculators, to enhance learning and provide immediate feedback.
20. Frequently Asked Questions (FAQs) About Decimals
Q: What is the difference between a decimal and a fraction?
A: A decimal is a number expressed in base-10 notation, with a whole number part and a fractional part separated by a decimal point. A fraction is a ratio of two integers, representing a part of a whole. Decimals and fractions are both ways to represent parts of a whole and can be converted to each other.
Q: How do you add decimals with different numbers of decimal places?
A: To add decimals with different numbers of decimal places, align the decimal points vertically and add zeros to the right of the numbers with fewer decimal places so that all numbers have the same number of decimal places. Then, add the numbers as you would with whole numbers, keeping the decimal point in the same position.
Q: What is a repeating decimal, and how do you convert it to a fraction?
A: A repeating decimal is a decimal number that has a repeating sequence of digits after the decimal point. To convert a repeating decimal to a fraction, use algebraic methods to eliminate the repeating part and solve for the fraction equivalent.
Q: How do you round a decimal to a specific number of decimal places?
A: To round a decimal, identify the digit to be rounded, look at the next digit to the right (the test digit), and apply the rounding rules: If the test digit is 0-4, round down; if the test digit is 5-9, round up. Then, drop the remaining digits to the right of the rounded digit.
Q: What are some real-world applications of decimals?
A: Decimals are used extensively in finance, measurement, science, cooking, and sports. They provide the precision needed for many everyday tasks, such as calculating prices, measuring length and weight, performing scientific calculations, and adjusting recipe measurements.
Understanding decimals is a fundamental skill that is essential for success in mathematics and everyday life. Whether you are calculating prices, measuring ingredients, or performing scientific calculations, decimals are an indispensable tool.
We hope this comprehensive guide has helped you gain a deeper understanding of what decimals are, how they work, and how they are used. Remember, if you ever have any questions or need further assistance, WHAT.EDU.VN is here to provide you with clear, concise, and helpful answers.
Do you have more questions about decimals or any other topic? Don’t hesitate to ask on WHAT.EDU.VN for free answers and expert insights. We’re here to help you learn and grow!
Our team of experts is always ready to provide you with the knowledge and support you need.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Don’t wait—ask your question today and unlock a world of knowledge at what.edu.vn