Are you curious about what constitutes a geometric progression? At WHAT.EDU.VN, we provide a straightforward explanation of geometric sequences, also known as geometric progressions. We will explore the common ratio, sequence formulas, and practical examples. Whether you’re looking for arithmetic sequences or a common difference, explore our resources for comprehensive learning!
1. What is a Geometric Sequence?
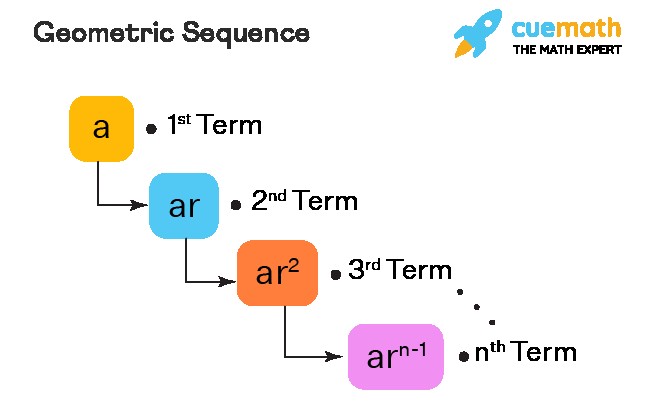
A geometric sequence, also known as a geometric progression, is a list of numbers where each term is found by multiplying the previous term by a constant value called the common ratio. This means that the ratio between any two consecutive terms in the sequence remains the same.
- The common ratio can be either positive or negative.
- If the common ratio is 1, then the sequence is constant.
- If the common ratio is -1, then the sequence alternates between two values.
For example, the sequence 2, 6, 18, 54,… is a geometric sequence because each term is obtained by multiplying the previous term by 3. The common ratio in this case is 3.
1.1 Finite Geometric Sequence
A finite geometric sequence is a geometric sequence with a limited number of terms. This means the sequence has a clear ending point. An example is:
2, 6, 18, 54, ..., 4374
Here, 4374 is the last term, making it a finite sequence.
1.2 Infinite Geometric Sequence
An infinite geometric sequence is a geometric sequence that continues indefinitely, without a defined last term. For instance:
2, -4, 8, -16, ...
This sequence goes on forever, thus it is an infinite geometric sequence.
Alt Text: Illustration depicting the general form of a geometric sequence, showing how each term is derived by multiplying the previous term by a constant ratio.
2. What Are the Key Geometric Sequence Formulas?
Here are the formulas that define the geometric sequence a, ar, ar², ar³,... :
- nth Term: an = ar^(n-1)
- Sum of n Terms: Sn = a(1-r^n)/(1-r) if r ≠ 1
- Sum to Infinity: S∞ = a/(1-r) if |r| < 1
Where:
ais the first term,ris the common ratio,nis the term number.
3. How to Determine the Nth Term of a Geometric Sequence?
The nth term of a geometric sequence is found using the formula:
an = a * r^(n-1)
Where:
anis the nth term,ais the first term,ris the common ratio,nis the term number.
3.1 Recursive Formula of Geometric Sequence
The recursive formula is an alternative way to find terms in a geometric sequence by using the term immediately before it. The formula is:
an = r * an-1
Where:
anis the nth term,ris the common ratio,an-1is the previous term (the (n-1)th term).
Example: Let’s say we want to find the 7th term of a geometric sequence where the first term (a1) is 3 and the common ratio (r) is 2. Using the formula:
a7 = 3 2^(7-1) = 3 2^6 = 3 * 64 = 192
So, the 7th term of this geometric sequence is 192.
4. What is the Formula for the Sum of a Finite Geometric Sequence?
The sum of the first n terms of a geometric sequence is given by the formula:
Sn = a * (1 – r^n) / (1 – r)
Where:
Snis the sum of the first n terms,ais the first term,ris the common ratio,nis the number of terms.
4.1 Deriving the Sum of Finite Geometric Sequence
To derive the formula for the sum of a finite geometric sequence, start with the sum:
Sn = a + ar + ar^2 + … + ar^(n-1)
Multiply both sides by r:
rSn = ar + ar^2 + ar^3 + … + ar^n
Subtract the second equation from the first:
Sn – rSn = a – ar^n
Factor out Sn on the left side:
Sn(1 – r) = a(1 – r^n)
Divide both sides by (1 - r) to solve for Sn:
Sn = a(1 – r^n) / (1 – r)
This formula allows you to calculate the sum of the first n terms of a geometric sequence.
5. How Do You Calculate the Sum of an Infinite Geometric Sequence?
The sum of an infinite geometric sequence is calculated using the formula:
S∞ = a / (1 – r)
This formula is valid only when the absolute value of the common ratio r is less than 1 (|r| < 1). If |r| ≥ 1, the series does not converge and does not have a finite sum.
5.1 Sum of Infinite Geometric Sequence Proof
To understand how the formula for the sum of an infinite geometric sequence is derived, start with the finite sum formula:
Sn = a(1 – r^n) / (1 – r)
As n approaches infinity, if |r| < 1, then r^n approaches 0. Thus, the formula simplifies to:
S∞ = a(1 – 0) / (1 – r) = a / (1 – r)
This is how you find the sum of an infinite geometric sequence when |r| < 1.
Alt Text: Image displaying the key formulas for geometric sequences, including the nth term, the sum of a finite sequence, and the sum of an infinite sequence, each labeled clearly for reference.
6. Geometric Sequence vs. Arithmetic Sequence
Geometric sequences and arithmetic sequences are both types of number sequences, but they differ in how terms are generated:
- Geometric Sequence: Each term is multiplied by a constant ratio (e.g., 2, 4, 8, 16…).
- Arithmetic Sequence: Each term is added by a constant difference (e.g., 2, 4, 6, 8…).
| Feature | Geometric Sequence | Arithmetic Sequence |
|---|---|---|
| Definition | Constant ratio between terms | Constant difference between terms |
| How to find next term | Multiply by a constant ratio | Add a constant difference |
| General form | a, ar, ar², ar³,… | a, a+d, a+2d, a+3d,… |
| Nth term formula | an = ar^(n-1) | an = a + (n-1)d |
| Sum of n terms | Sn = a(1-r^n)/(1-r) if r ≠ 1 | Sn = n/2 [2a + (n-1)d] |
| Convergence | Converges if | r |


7. Geometric Sequence Examples
Example 1: Find the 10th term of the geometric sequence 3, 6, 12, 24, …
- Solution:
- First term (a) = 3
- Common ratio (r) = 6/3 = 2
- n = 10
- Using the formula an = ar^(n-1):
- a10 = 3 2^(10-1) = 3 2^9 = 3 * 512 = 1536
- Answer: The 10th term is 1536.
Example 2: Calculate the sum of the first 5 terms of the geometric sequence 1, 2, 4, 8, …
- Solution:
- First term (a) = 1
- Common ratio (r) = 2/1 = 2
- n = 5
- Using the formula Sn = a(1 – r^n) / (1 – r):
- S5 = 1 * (1 – 2^5) / (1 – 2) = (1 – 32) / (-1) = (-31) / (-1) = 31
- Answer: The sum of the first 5 terms is 31.
Example 3: Determine the sum of the infinite geometric sequence 4, 2, 1, 1/2, …
- Solution:
- First term (a) = 4
- Common ratio (r) = 2/4 = 1/2
- Since |r| < 1, we can use the formula S∞ = a / (1 – r):
- S∞ = 4 / (1 – 1/2) = 4 / (1/2) = 4 * 2 = 8
- Answer: The sum of the infinite geometric sequence is 8.
Alt Text: A teacher helping a student with a math problem on a laptop, illustrating personalized learning and problem-solving support.
8. Practice Questions on Geometric Sequence
Here are a couple of questions on geometric sequences for practice:
- Find the 8th term of the geometric sequence 5, 10, 20, 40, …
- Calculate the sum of the first 6 terms of the geometric sequence 3, 9, 27, 81, …
(Scroll down for answers)
9. FAQs on Geometric Sequence
9.1 What is the Definition of a Geometric Sequence?
A geometric sequence is a sequence in which the ratio between successive terms is constant. This ratio is known as the common ratio.
9.2 How Do You Find the Nth Term of a Geometric Sequence?
To find the nth term of a geometric sequence, use the formula:
an = a * r^(n-1)
Where:
anis the nth term,ais the first term,ris the common ratio,nis the term number.
9.3 What is ‘r’ in the Geometric Sequence Formula?
In the geometric sequence formula, r represents the common ratio between consecutive terms.
9.4 When Does a Geometric Sequence Diverge?
A geometric sequence diverges when the absolute value of the common ratio r is greater than or equal to 1 (i.e., |r| ≥ 1).
9.5 What is the Meaning of the Common Ratio of a Geometric Sequence?
The common ratio is the constant factor by which each term is multiplied to get the next term in the sequence.
9.6 How Do You Find the Sum of a Finite Geometric Sequence?
The sum of a finite geometric sequence is found using the formula:
Sn = a * (1 – r^n) / (1 – r)
Where:
Snis the sum of the first n terms,ais the first term,ris the common ratio,nis the number of terms.
9.7 What are the Geometric Sequence Formulas?
The primary geometric sequence formulas include:
- Nth term: an = a * r^(n-1)
- Sum of n terms (finite): Sn = a * (1 – r^n) / (1 – r)
- Sum to infinity (infinite): S∞ = a / (1 – r) (only when |r| < 1)
9.8 How Do You Find the Sum of an Infinite Geometric Sequence?
To find the sum of an infinite geometric sequence, use the formula:
S∞ = a / (1 – r)
This formula is applicable only if the absolute value of the common ratio r is less than 1 (|r| < 1).
9.9 When Does a Geometric Sequence Converge?
A geometric sequence converges when the absolute value of the common ratio r is less than 1 (i.e., |r| < 1).
(Answers to Practice Questions)
- The 8th term of the geometric sequence 5, 10, 20, 40, … is 640.
- The sum of the first 6 terms of the geometric sequence 3, 9, 27, 81, … is 1092.
Do you have any questions or need more clarification on geometric sequences? Don’t hesitate! Visit WHAT.EDU.VN to ask your questions and receive free answers. Our community of experts is ready to assist you with any topic. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or via WhatsApp at +1 (206) 555-7890. Explore the possibilities with what.edu.vn today!