What Is A Hexagon? Discover the definition of a hexagon, explore its fascinating properties, and learn about its many applications with WHAT.EDU.VN. Unlock the secrets of this six-sided shape and enhance your geometric understanding. Delve into its role in various fields such as architecture, nature, and technology.
1. Understanding the Hexagon: A Comprehensive Definition
A hexagon, at its core, is a polygon characterized by six sides, six vertices (corners), and six angles. This geometric shape belongs to the broader family of polygons, distinguished by its unique six-sided structure. The term “hexagon” originates from the Greek words “hex,” meaning six, and “gon,” meaning angle or side. At WHAT.EDU.VN we make geometry accessible to everyone.
1.1. Types of Hexagons: Regular vs. Irregular
Hexagons are not all created equal; they come in two primary forms: regular and irregular.
-
Regular Hexagon: A regular hexagon is defined by its six congruent sides (all sides are of equal length) and six congruent angles (all angles are of equal measure, each being 120 degrees). This symmetry gives regular hexagons a pleasing and balanced appearance.
-
Irregular Hexagon: In contrast, an irregular hexagon has sides and angles of varying lengths and measures. While it still maintains the six-sided structure, it lacks the uniform properties of a regular hexagon.
1.2. Key Properties of a Hexagon
Understanding the properties of a hexagon is crucial to appreciating its geometric significance. Here are some of the key attributes:
- Number of Sides: As the name suggests, a hexagon has six sides.
- Number of Vertices: It also has six vertices, which are the points where the sides meet.
- Number of Angles: A hexagon features six interior angles.
- Sum of Interior Angles: The sum of the interior angles of a hexagon is always 720 degrees. In a regular hexagon, each interior angle measures 120 degrees.
- Diagonals: A hexagon has nine diagonals, which are line segments connecting non-adjacent vertices.
1.3. Hexagons in Nature and Everyday Life
Hexagons are not confined to textbooks and geometry lessons; they appear frequently in the natural world and various aspects of our daily lives:
- Honeycomb: Perhaps the most iconic example of hexagons in nature is the honeycomb. Bees construct their honeycombs using hexagonal cells because this shape efficiently maximizes space and requires minimal material.
- Snowflakes: While snowflakes exhibit intricate and diverse patterns, many of them possess a basic hexagonal structure due to the way water molecules freeze.
- Basalt Columns: In certain geological formations, such as the Giant’s Causeway in Northern Ireland, basalt columns naturally fracture into hexagonal shapes as they cool.
- Nuts and Bolts: Many nuts and bolts are designed with hexagonal heads to provide a secure grip for wrenches.
- Floor Tiles: Hexagonal tiles can be used to create visually appealing and geometrically interesting floor patterns.
1.4. Mathematical Formulas for Hexagons
To delve deeper into the mathematical properties of hexagons, here are some useful formulas:
-
Area of a Regular Hexagon: The area (A) of a regular hexagon with side length “s” can be calculated using the formula:
A = (3√3 / 2) * s^2
-
Perimeter of a Regular Hexagon: The perimeter (P) of a regular hexagon with side length “s” is simply:
P = 6s
-
Apothem of a Regular Hexagon: The apothem (a) is the distance from the center of the hexagon to the midpoint of a side. It can be calculated as:
a = (√3 / 2) * s
1.5. Constructing a Hexagon
Creating your own hexagon is a fun and educational exercise. Here’s how to construct a regular hexagon using a compass and straightedge:
- Draw a Circle: Start by drawing a circle with your compass. This circle will determine the size of your hexagon.
- Mark a Point: Choose any point on the circle’s circumference as your starting point.
- Maintain Compass Width: Without changing the compass width, place the compass point on the starting point and make an arc that intersects the circle.
- Repeat: Move the compass point to the intersection point and make another arc on the circle. Repeat this process until you have six equally spaced points on the circle.
- Connect the Points: Use a straightedge to connect the six points in order around the circle. The resulting figure is a regular hexagon.
Do you have any questions about hexagon construction or other geometric shapes? Ask them on WHAT.EDU.VN and get answers for free.
2. Exploring the Uses and Applications of Hexagons
Hexagons are more than just geometric shapes; they have a wide range of practical applications in various fields, from architecture and engineering to nature and art. Their unique properties, such as their ability to tessellate (fit together without gaps) and their high strength-to-weight ratio, make them valuable in many contexts.
2.1. Hexagons in Architecture and Construction
Hexagons have been used in architecture for centuries, both for their aesthetic appeal and their structural advantages.
- Honeycomb Structures: Architects and engineers often draw inspiration from the honeycomb structure found in nature. Hexagonal cells provide excellent support and strength while minimizing the amount of material needed. This design is used in roofing, flooring, and wall panels.
- Geodesic Domes: Geodesic domes, popularized by Buckminster Fuller, are spherical or hemispherical structures made up of interconnected polygons, including hexagons. These domes are lightweight, strong, and can cover large areas without the need for internal supports.
- Hexagonal Tiles: Hexagonal tiles are a popular choice for flooring and wall coverings due to their unique shape and ability to create interesting patterns. They can be arranged in various ways to add visual appeal to a space.
2.2. Hexagons in Engineering and Technology
Hexagons also play a significant role in engineering and technology.
- Nuts and Bolts: The hexagonal shape of nuts and bolts is designed to provide a secure grip for wrenches. The six sides allow for easy tightening and loosening, while also distributing the force evenly around the fastener.
- Microstructures: In materials science, hexagonal microstructures are used to enhance the properties of materials. For example, graphene, a single layer of carbon atoms arranged in a hexagonal lattice, is incredibly strong and lightweight.
- Cellular Networks: In telecommunications, hexagonal cell towers are used to create efficient and reliable cellular networks. The hexagonal shape allows for maximum coverage with minimal overlap between cells.
2.3. Hexagons in Nature
As mentioned earlier, hexagons are abundant in nature.
- Honeycomb: Bees construct their honeycombs using hexagonal cells because this shape is the most efficient way to store honey and raise their young. The hexagonal structure maximizes space and requires minimal wax.
- Snowflakes: The hexagonal symmetry of snowflakes is due to the way water molecules arrange themselves when freezing. While each snowflake is unique, they all share a basic hexagonal structure.
- Basalt Columns: The hexagonal columns found in geological formations like the Giant’s Causeway are formed by the cooling and contraction of basalt lava.
2.4. Hexagons in Art and Design
Hexagons have also been used in art and design for their aesthetic qualities.
- Mosaics: Hexagonal tiles can be used to create intricate mosaic patterns. Their unique shape allows for a wide variety of designs and arrangements.
- Geometric Art: Many artists use hexagons in their geometric artwork. The shape’s symmetry and balance can create visually appealing and harmonious compositions.
- Logos and Branding: Some companies incorporate hexagons into their logos and branding to convey a sense of stability, strength, and innovation.
2.5. Hexagons in Games and Puzzles
Hexagons are also found in various games and puzzles.
- Board Games: Games like Settlers of Catan use hexagonal tiles to create a modular game board. The hexagonal shape allows for easy arrangement and expansion of the board.
- Puzzles: Hexagonal puzzles, such as tangrams, challenge players to arrange hexagonal pieces to form different shapes and patterns.
- Video Games: Hexagons are sometimes used in video game maps and interfaces to represent terrain or other game elements.
Are you looking for more information about the applications of hexagons or other geometric shapes? Visit WHAT.EDU.VN and ask your questions today for free.
3. The Geometry of Hexagons: Angles, Sides, and Area
To fully understand hexagons, it’s essential to delve into their geometric properties. This involves exploring the relationships between their angles, sides, and area.
3.1. Interior and Exterior Angles of a Hexagon
A hexagon has six interior angles and six exterior angles. The sum of the interior angles of a hexagon is always 720 degrees. In a regular hexagon, each interior angle measures 120 degrees.
The exterior angles of a hexagon are the angles formed by extending one side of the hexagon and measuring the angle between the extended side and the adjacent side. The sum of the exterior angles of any polygon, including a hexagon, is always 360 degrees. In a regular hexagon, each exterior angle measures 60 degrees.
3.2. Calculating the Area of a Regular Hexagon
The area of a regular hexagon can be calculated using the formula:
A = (3√3 / 2) * s^2
Where “A” is the area and “s” is the length of one side of the hexagon.
This formula is derived from the fact that a regular hexagon can be divided into six equilateral triangles. The area of each equilateral triangle is (√3 / 4) s^2, and since there are six triangles, the total area of the hexagon is (6 √3 / 4) s^2, which simplifies to (3√3 / 2) s^2.
3.3. Calculating the Perimeter of a Regular Hexagon
The perimeter of a regular hexagon is simply the sum of the lengths of its six sides. Since all sides of a regular hexagon are equal in length, the perimeter can be calculated using the formula:
P = 6s
Where “P” is the perimeter and “s” is the length of one side of the hexagon.
3.4. Diagonals of a Hexagon
A hexagon has nine diagonals, which are line segments connecting non-adjacent vertices. The diagonals of a regular hexagon have different lengths, depending on which vertices they connect.
- Short Diagonals: These connect vertices that are two positions apart. In a regular hexagon, all short diagonals are of equal length.
- Long Diagonals: These connect vertices that are three positions apart. In a regular hexagon, all long diagonals are of equal length.
The length of the short diagonals can be calculated using the formula:
d_short = s√3
Where “d_short” is the length of the short diagonal and “s” is the length of one side of the hexagon.
The length of the long diagonals is simply twice the length of one side of the hexagon:
d_long = 2s
Where “d_long” is the length of the long diagonal and “s” is the length of one side of the hexagon.
3.5. Symmetry of a Hexagon
A regular hexagon has several types of symmetry:
- Rotational Symmetry: A regular hexagon has rotational symmetry of order 6. This means that it can be rotated by 60 degrees (360/6) and still look the same.
- Reflectional Symmetry: A regular hexagon has reflectional symmetry across six lines: three lines that pass through opposite vertices and three lines that pass through the midpoints of opposite sides.
These symmetries contribute to the aesthetic appeal and mathematical properties of regular hexagons.
Do you need help with geometry problems or want to learn more about geometric shapes? Visit WHAT.EDU.VN and get free answers to your questions.
4. Hexagons in Advanced Mathematics and Science
Hexagons are not just elementary geometric shapes; they also appear in advanced mathematics and scientific research.
4.1. Tessellations and Tilings
A tessellation, or tiling, is a pattern made up of one or more shapes that cover a plane without any gaps or overlaps. Regular hexagons are one of only three regular polygons that can tessellate the plane (the other two are equilateral triangles and squares).
The ability of hexagons to tessellate makes them useful in various applications, such as flooring, wall coverings, and mosaics.
4.2. Honeycomb Conjecture
The honeycomb conjecture states that the hexagonal grid is the most efficient way to divide a surface into regions of equal area with the least total perimeter. This conjecture was proven mathematically in 1999 by Thomas Hales.
The honeycomb conjecture explains why bees construct their honeycombs using hexagonal cells. The hexagonal shape maximizes the amount of honey that can be stored while minimizing the amount of wax needed to build the cells.
4.3. Hexagonal Close Packing
In materials science, hexagonal close packing (HCP) is one of the two most common ways to pack spheres together in a three-dimensional space (the other being cubic close packing). In HCP, each sphere is surrounded by 12 other spheres, forming a hexagonal lattice.
HCP is found in many metals, such as titanium, zinc, and magnesium. The HCP structure gives these materials their unique properties, such as high strength and ductility.
4.4. Graphene
Graphene is a single layer of carbon atoms arranged in a hexagonal lattice. It is one of the strongest and lightest materials known to science. Graphene has a wide range of potential applications, including electronics, energy storage, and biomedical engineering.
The hexagonal structure of graphene gives it its unique properties. The strong covalent bonds between the carbon atoms in the hexagonal lattice make graphene incredibly strong.
4.5. Fullerenes
Fullerenes are molecules made entirely of carbon atoms in the form of a hollow sphere, ellipsoid, or tube. The most famous fullerene is buckminsterfullerene (C60), which has a structure similar to a soccer ball, with 20 hexagons and 12 pentagons.
Fullerenes have a wide range of potential applications, including drug delivery, catalysis, and materials science.
Do you have complex math or science questions that you need answered? Visit WHAT.EDU.VN and ask our experts for free.
5. Frequently Asked Questions (FAQs) About Hexagons
Here are some frequently asked questions about hexagons:
| Question | Answer |
|---|---|
| What is the difference between a regular and an irregular hexagon? | A regular hexagon has six equal sides and six equal angles, while an irregular hexagon has sides and angles of different lengths and measures. |
| How do you calculate the area of a regular hexagon? | The area of a regular hexagon can be calculated using the formula: A = (3√3 / 2) * s^2, where “A” is the area and “s” is the length of one side. |
| What is the sum of the interior angles of a hexagon? | The sum of the interior angles of a hexagon is always 720 degrees. |
| How many diagonals does a hexagon have? | A hexagon has nine diagonals. |
| Where can you find hexagons in nature? | Hexagons can be found in honeycombs, snowflakes, and basalt columns. |
| What is the honeycomb conjecture? | The honeycomb conjecture states that the hexagonal grid is the most efficient way to divide a surface into regions of equal area with the least total perimeter. |
| What is graphene? | Graphene is a single layer of carbon atoms arranged in a hexagonal lattice. It is one of the strongest and lightest materials known to science. |
| What are fullerenes? | Fullerenes are molecules made entirely of carbon atoms in the form of a hollow sphere, ellipsoid, or tube. The most famous fullerene is buckminsterfullerene (C60), which has a structure similar to a soccer ball, with 20 hexagons and 12 pentagons. |
| How do you construct a regular hexagon? | A regular hexagon can be constructed using a compass and straightedge by drawing a circle, marking six equally spaced points on the circumference, and connecting the points with straight lines. |
| Why are hexagons used in nuts and bolts? | The hexagonal shape of nuts and bolts provides a secure grip for wrenches, allowing for easy tightening and loosening while distributing the force evenly around the fastener. |
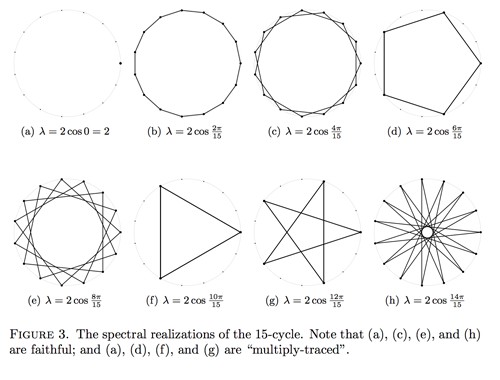
6. Real-World Examples of Hexagons
Hexagons are not just theoretical shapes; they are found in many real-world applications. Here are some examples:
- Honeycomb: Bees build honeycombs with hexagonal cells to efficiently store honey and pollen. The hexagonal shape maximizes space and minimizes the amount of wax needed.
- Nuts and Bolts: The hexagonal shape of nuts and bolts allows for easy tightening and loosening with a wrench. The six sides provide a good grip and distribute the force evenly.
- Graphene: This material, made of a single layer of carbon atoms arranged in a hexagonal lattice, is incredibly strong and lightweight, making it useful in various applications.
- Geodesic Domes: These structures, often made of interconnected hexagons and other polygons, are strong and lightweight, making them ideal for covering large areas.
- Snowflakes: The intricate patterns of snowflakes often exhibit hexagonal symmetry due to the way water molecules freeze.
- Basalt Columns: These geological formations, found in places like the Giant’s Causeway in Northern Ireland, are naturally fractured into hexagonal shapes as they cool.
- Floor Tiles: Hexagonal tiles can be used to create visually appealing and geometrically interesting floor patterns.
These are just a few examples of how hexagons are used in the real world. Their unique properties make them valuable in various fields, from nature to engineering to art.
7. How to Draw a Perfect Hexagon
Drawing a perfect hexagon can seem daunting, but with the right tools and techniques, it’s easier than you might think. Here’s a step-by-step guide:
- Gather Your Tools: You’ll need a compass, a straightedge (ruler), and a pencil.
- Draw a Circle: Use the compass to draw a circle. This circle will determine the size of your hexagon.
- Mark a Point: Choose any point on the circle’s circumference as your starting point.
- Maintain Compass Width: Without changing the compass width, place the compass point on the starting point and make an arc that intersects the circle.
- Repeat: Move the compass point to the intersection point and make another arc on the circle. Repeat this process until you have six equally spaced points on the circle.
- Connect the Points: Use the straightedge to connect the six points in order around the circle. The resulting figure is a regular hexagon.
Tips for Drawing a Perfect Hexagon:
- Keep the Compass Width Consistent: The most important thing is to keep the compass width the same throughout the entire process. This will ensure that all the sides of the hexagon are equal in length.
- Use a Sharp Pencil: A sharp pencil will help you draw precise lines and arcs.
- Be Patient: Take your time and be careful to accurately mark the points on the circle.
With practice, you’ll be able to draw perfect hexagons every time.
8. The Significance of Hexagons in Different Cultures
Hexagons, while primarily a geometric shape, have also found symbolic significance in various cultures throughout history.
- Ancient Greece: In ancient Greece, hexagons were associated with harmony and balance. They were often used in architectural designs and decorative patterns.
- Native American Cultures: Some Native American tribes used hexagonal patterns in their art and weaving. The hexagon represented the interconnectedness of all things and the harmony between humans and nature.
- Christianity: In Christian symbolism, the hexagon can represent the six days of creation. It is sometimes used in church architecture and stained glass windows.
- Modern Symbolism: In modern times, hexagons are often used to represent technology, innovation, and efficiency. They can be found in logos, branding, and designs for various products and services.
The symbolic meaning of hexagons varies depending on the culture and context. However, they often represent harmony, balance, interconnectedness, and innovation.
9. Common Mistakes to Avoid When Working with Hexagons
When working with hexagons, it’s easy to make mistakes, especially if you’re new to geometry. Here are some common mistakes to avoid:
- Assuming All Hexagons Are Regular: Not all hexagons are regular. Make sure to check if the hexagon has equal sides and angles before applying formulas or theorems that only apply to regular hexagons.
- Incorrectly Calculating the Area: The area of a regular hexagon is not simply the product of the side length and the number of sides. Use the correct formula: A = (3√3 / 2) * s^2.
- Confusing Diagonals with Sides: Diagonals are line segments that connect non-adjacent vertices, while sides are the line segments that form the perimeter of the hexagon.
- Not Keeping the Compass Width Consistent: When constructing a hexagon with a compass and straightedge, it’s crucial to keep the compass width the same throughout the entire process.
- Ignoring the Properties of Regular Hexagons: Regular hexagons have specific properties, such as equal sides, equal angles, and rotational and reflectional symmetry. Make sure to take these properties into account when solving problems or creating designs.
By avoiding these common mistakes, you can improve your accuracy and understanding when working with hexagons.
10. Further Exploration of Hexagons
If you’re interested in learning more about hexagons, here are some resources to explore:
- Books: Look for books on geometry, tessellations, and geometric design.
- Websites: Search for websites that offer tutorials, interactive tools, and information about hexagons and other geometric shapes.
- Online Courses: Consider taking an online course on geometry or related topics.
- Museums: Visit museums that feature exhibits on mathematics, science, and art.
- Math Clubs: Join a math club or participate in math competitions.
Learning about hexagons can be a fun and rewarding experience. By exploring these resources, you can deepen your understanding of this fascinating geometric shape and its many applications.
Still have questions about hexagons? Don’t hesitate to ask them on WHAT.EDU.VN. Our community of experts is ready to help you learn and explore the world of geometry for free.
At WHAT.EDU.VN, we understand that finding answers to your questions can be challenging. That’s why we’ve created a platform where you can ask any question and receive free, accurate, and easy-to-understand answers. Whether you’re a student, a professional, or simply curious about the world around you, WHAT.EDU.VN is here to help.
We are located at 888 Question City Plaza, Seattle, WA 98101, United States. You can reach us via Whatsapp at +1 (206) 555-7890 or visit our website at WHAT.EDU.VN.
Don’t let your questions go unanswered. Visit what.edu.vn today and start exploring the world of knowledge.