A linear pair is a fundamental concept in geometry, referring to two adjacent angles that form a straight line, and you can explore this topic further at WHAT.EDU.VN. This means their measures add up to 180 degrees, making them supplementary angles. Understanding linear pairs is essential for solving various geometry problems and grasping related concepts like supplementary angles and angle relationships. Are you struggling to understand linear pair angles? At WHAT.EDU.VN, we make geometry easier for you!
1. Understanding the Linear Pair of Angles: A Comprehensive Definition
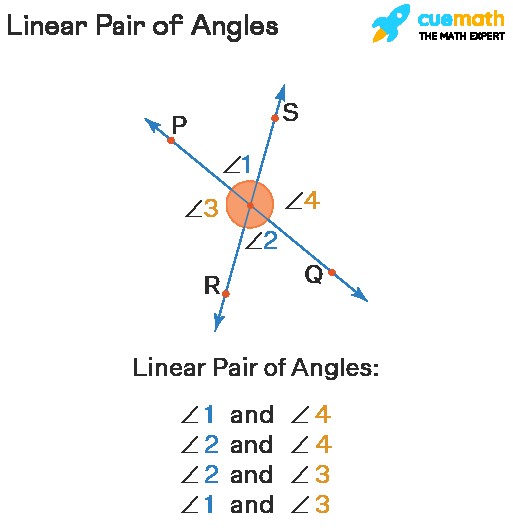
A linear pair of angles is formed when two lines intersect at a single point, creating two adjacent angles. The term “adjacent” means the angles share a common vertex (corner point) and a common arm (side), but do not overlap. Critically, the two angles must lie on a straight line. This arrangement dictates a crucial property: the angles in a linear pair are supplementary, meaning their measures add up to 180°. Essentially, a linear pair of angles always sums to 180 degrees.
2. Key Properties That Define Linear Pairs of Angles
Linear pairs possess unique characteristics that distinguish them from other angle relationships. Understanding these properties is crucial for identifying and working with linear pairs in geometry problems. Here’s a breakdown of the key properties:
- Adjacency: The angles must be adjacent, meaning they share a common vertex and a common side, without overlapping.
- Supplementary: The angles must be supplementary, meaning their measures add up to 180 degrees. They form a straight line.
- Common Vertex and Arm: Linear pair angles share a common vertex (the point where the two lines intersect) and a common arm (the line segment that connects the vertex to a point on each line).
- Non-Common Arms Form a Straight Line: The two non-common arms of the linear pair angles form a straight line. This is a defining characteristic of a linear pair.
- Not Always Congruent: While they are always supplementary, linear pair angles are not always congruent (equal in measure). They are only congruent when each angle measures 90 degrees, forming two right angles.
3. Linear Pair of Angles vs. Supplementary Angles: Spotting the Key Differences
In geometry, both linear pairs and supplementary angles involve angles whose measures add up to 180 degrees. However, there’s a crucial distinction between them: adjacency.
| Feature | Linear Pair of Angles | Supplementary Angles |
|---|---|---|
| Adjacency | Always adjacent; share a common vertex and a common arm, lying next to each other. | Not necessarily adjacent; can be located anywhere. |
| Relationship | All linear pairs are supplementary angles. | Not all supplementary angles are linear pairs. |
| Example | ∠1 and ∠2 in the image below (adjacent and sum to 180°). | ∠A and ∠B, ∠1 and ∠2 (∠A and ∠B are not adjacent, but their sum is 180°). |
| Definition | A pair of adjacent angles whose sum is 180 degrees, sharing a common vertex and a common arm. | Two angles whose sum is 180 degrees, regardless of their position relative to each other. |
| Visual | Two angles forming a straight line. | Two angles that may or may not be near each other. |
| Key Criterion | Angles must be adjacent and share a common side. | Only the sum of the angles must be 180 degrees. |
| Use in Proofs | Often used in geometric proofs where adjacency and the straight line property are important. | Used when only the sum of the angles is relevant, and adjacency is not a factor. |
| Scope | More restrictive; requires both adjacency and a sum of 180 degrees. | More general; only requires that the sum of the angles be 180 degrees. |
| Requirements | Must be adjacent to each other, sharing a common vertex and a common side. | Not required to be next to each other; may be separate and distinct angles. |
| Representation | Typically represented as angles along a straight line, clearly showing their adjacent nature. | Can be represented as two separate angles, emphasizing that it is their measures, not their position, that make them supplementary. |
| Association | Intimately linked with geometric layouts involving intersecting lines. | Used in broader contexts where angular measures are essential, regardless of the geometric configuration. |
| Practical Use | Essential for problems involving adjacent angles and line segments in geometric figures. | Applied in scenarios where the primary focus is on the sum of the angle measures, applicable in abstract mathematical contexts and practical problems alike. |
| Foundational Role | Forms a foundational concept in understanding more complex geometric relationships involving angles and lines. | Provides a basic understanding of angular relationships and properties that is foundational in more abstract angular geometry. |
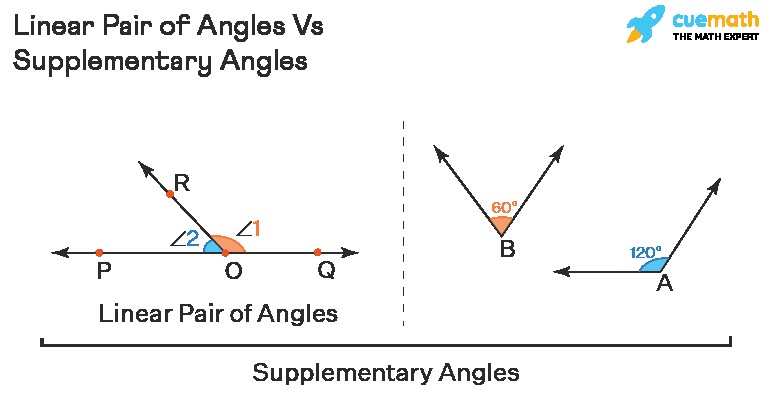
In the image above, both pairs of angles are supplementary, but ∠A and ∠B are not a linear pair because they are not adjacent.
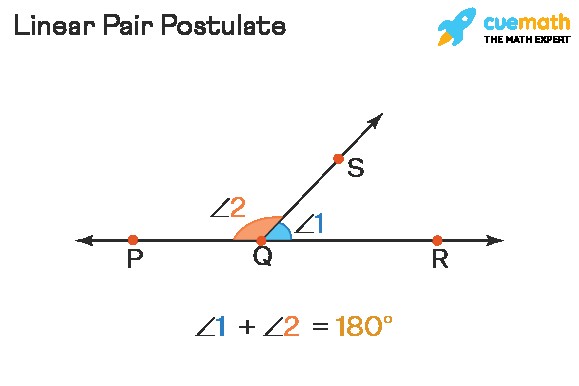
4. The Linear Pair Postulate: A Fundamental Truth
The linear pair postulate is a foundational statement in geometry that formalizes the relationship between a line and the angles formed when a ray intersects it.
The Postulate:
If a ray stands on a line, then the sum of the two adjacent angles formed is 180°.
What This Means:
Imagine a straight line. Now, picture another line (a ray) intersecting the first line at any point. This intersection creates two adjacent angles. The linear pair postulate states that these two angles will always add up to 180 degrees.
Converse of the Postulate:
The converse of the linear pair postulate is also true: If the sum of a pair of adjacent angles is 180°, then the non-common arms of the two angles form a line.
Linear Pair Axiom:
These two statements (the postulate and its converse) are often grouped together as the linear pair axiom.
Example:
In the figure below, ray QS stands on line PR, forming a linear pair of angles ∠1 and ∠2. According to the linear pair postulate, ∠1 + ∠2 = 180°.
Key Takeaways:
- The linear pair postulate is a fundamental truth in geometry.
- It states that angles in a linear pair are always supplementary.
- The postulate and its converse form the linear pair axiom.
- This concept is crucial for solving problems involving angles and lines.
5. Linear Pair of Angles: Examples
Let’s explore some examples to solidify your understanding of linear pairs.
Example 1:
If one of the angles forming a linear pair is a right angle (90°), then what can you say about the other angle?
Solution:
Let the two angles be ‘a’ and ‘b’. We know that ∠a + ∠b = 180° because they form a linear pair.
Given that ∠a = 90°, we can substitute this value into the equation:
90° + ∠b = 180°
Solving for ∠b:
∠b = 180° – 90°
∠b = 90°
Therefore, if one angle in a linear pair is a right angle, the other angle is also a right angle.
Example 2:
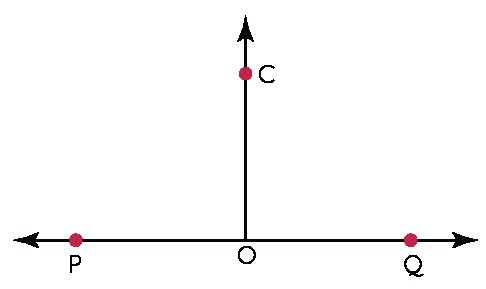
In the figure, POQ is a straight line, and ∠POC = ∠COQ. Show that ∠POC = 90°.
Solution:
Since ray OC stands on line PQ, by the linear pair axiom:
∠POC + ∠COQ = 180°
We are given that ∠POC = ∠COQ. Substituting this into the equation:
∠POC + ∠POC = 180°
2∠POC = 180°
∠POC = 180°/2 = 90°
Therefore, ∠POC = 90°.
Example 3:
Two angles forming a linear pair are in the ratio of 4:5. Find the measure of each angle.
Solution:
Let the two angles be 4y and 5y. Since they form a linear pair:
4y + 5y = 180°
9y = 180°
y = 180°/9 = 20°
Therefore, the two angles are:
4y = 4 * 20° = 80°
5y = 5 * 20° = 100°
6. Practice Questions on Linear Pair of Angles
(Note: The specific questions and answers were not provided in the original extract. You would need to create these based on the concepts explained.)
7. FAQs About Linear Pair of Angles
7.1. What Exactly Is a Linear Pair of Angles?
A linear pair consists of two adjacent angles that add up to 180 degrees. They share a common vertex and side, forming a straight line.
7.2. How Can You Determine the Linear Pair of an Angle?
To find the linear pair of an angle, subtract its measure from 180 degrees. For example, the linear pair of 60° is 120° (180° – 60° = 120°).
7.3. Is a Linear Pair Always Supplementary?
Yes, by definition, a linear pair is always supplementary because the two angles add up to 180 degrees.
7.4. How Many Angles Make Up a Linear Pair?
A linear pair always consists of two adjacent angles.
7.5. Are Linear Pair of Angles Always Congruent?
No, linear pair angles are not always congruent. They are only congruent if each angle measures 90 degrees.
7.6. Is It Possible for Three Angles to Form a Linear Pair?
No, a linear pair is defined as two adjacent angles that form a straight line (180 degrees). While three angles can be supplementary (add up to 180 degrees), they cannot form a linear pair unless two of them combine to act as one angle in the pair.
Unlock Your Geometry Potential at WHAT.EDU.VN
Do you find yourself struggling with geometry concepts? Are you looking for clear, concise explanations and expert guidance? Look no further than WHAT.EDU.VN!
At WHAT.EDU.VN, we understand the challenges students face when learning geometry. That’s why we offer a comprehensive platform with a wealth of resources to help you master this essential subject. Whether you’re grappling with linear pairs, struggling with proofs, or simply want to deepen your understanding of geometric principles, WHAT.EDU.VN has you covered.
Here’s how WHAT.EDU.VN can help you:
- Clear and Concise Explanations: We break down complex geometric concepts into easy-to-understand terms, using visuals and examples to illustrate key ideas.
- Step-by-Step Solutions: Get detailed, step-by-step solutions to a wide range of geometry problems, so you can see how to apply the concepts you’re learning.
- Personalized Support: Connect with our team of experienced geometry tutors who can provide personalized support and answer your questions.
- Interactive Practice: Test your knowledge with interactive quizzes and exercises that provide immediate feedback, so you can identify areas where you need more practice.
Don’t let geometry be a source of frustration. Join the WHAT.EDU.VN community today and unlock your geometry potential!
Ready to take the next step?
Visit WHAT.EDU.VN now and start exploring our extensive collection of geometry resources. And if you have any questions, our friendly support team is always here to help.
Contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
At WHAT.EDU.VN, we’re committed to making learning geometry easy, accessible, and enjoyable for everyone. Are you ready to experience the difference? Ask your questions for free on what.edu.vn
