What Is A One-To-One Function? A Comprehensive Guide

Are you scratching your head, trying to figure out what a one-to-one function is? WHAT.EDU.VN is here to clear up any confusion with a simple explanation. A one-to-one function, also known as an injective function, ensures that each element in its range corresponds to only one element in its domain. Keep reading to explore the properties, tests, and real-world applications of one-to-one functions, empowering you with a deep understanding of mathematical concepts like injective function, horizontal line test and inverse functions.

1. What is a One-to-One Function?

A one-to-one function, also known as an injective function, is a function where each element of the range corresponds to exactly one element of the domain; put simply, no two elements in the domain map to the same element in the range. This means that if you have a one-to-one function, each input will give you a unique output. It’s like a perfect pairing where everyone gets a unique partner.

1.1. One-to-One Function Definition

A one-to-one function, sometimes called an injective function, is a function in which every element of the range corresponds to exactly one element in the domain. This means that no two different elements in the domain produce the same output. In simpler terms, if f(x1) = f(x2), then x1 must equal x2.

Algebraically, this definition can be expressed as follows:

A function f: A -> B is one-to-one if and only if for all x1, x2 ∈ A, f(x1) = f(x2) implies x1 = x2.

The contrapositive of this definition is also useful:

If x1 ≠ x2, then f(x1) ≠ f(x2).

For instance, consider the function f(x) = x + 3. This is a one-to-one function because for every input x, there is a unique output f(x). If f(x1) = f(x2), then x1 + 3 = x2 + 3, which simplifies to x1 = x2.

On the other hand, the function f(x) = x^2 is not a one-to-one function. For example, f(2) = 4 and f(-2) = 4. Here, two different inputs, 2 and -2, produce the same output, 4, violating the one-to-one condition. Functions that are not one-to-one are often referred to as many-to-one functions.

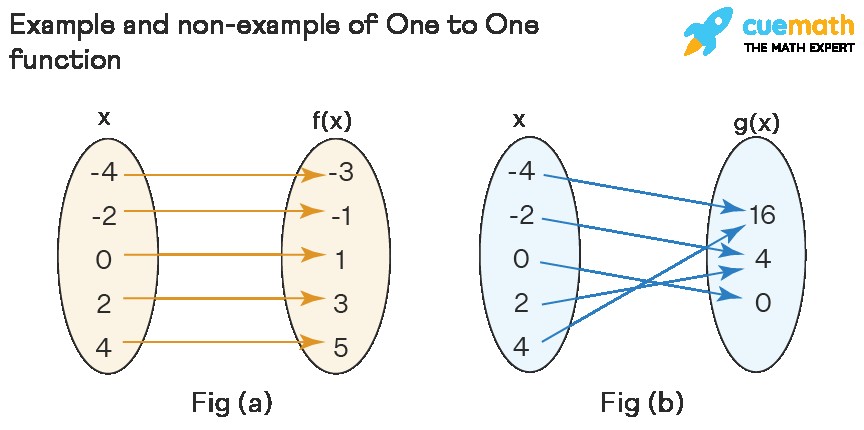
The figure above illustrates the concept of one-to-one functions using mapping diagrams. In the one-to-one function (a), each element in the domain x maps to a unique element in the codomain f(x). In contrast, the function that is not one-to-one (b) shows that different elements in the domain x (e.g., 2 and -2) map to the same element in the codomain g(x), demonstrating it’s not a one-to-one function.

1.2. Examples of One-to-One Functions

To further clarify the concept, let’s consider several examples of functions and determine whether they are one-to-one:

1. Linear Function: f(x) = 2x + 1

   • This function is one-to-one. If f(x1) = f(x2), then 2x1 + 1 = 2x2 + 1. Subtracting 1 from both sides gives 2x1 = 2x2, and dividing by 2 results in x1 = x2.

2. Exponential Function: f(x) = e^x

   • This function is one-to-one. The exponential function is always increasing, and each input x produces a unique output f(x).

3. Cubic Function: f(x) = x^3

   • This function is one-to-one. If f(x1) = f(x2), then x1^3 = x2^3. Taking the cube root of both sides gives x1 = x2.

4. Function: f(x) = |x| (absolute value function)

   • This function is not one-to-one. For example, f(3) = 3 and f(-3) = 3. Two different inputs (3 and -3) produce the same output (3).

5. Function: f(x) = sin(x)

   • This function is not one-to-one. For example, f(0) = 0 and f(π) = 0. Over the interval [0, 2π], the sine function takes on the same value for multiple inputs.

1.3. Real-World Examples

One-to-one functions aren’t just theoretical concepts; they exist in the real world.

• Social Security Numbers: Each person in the United States is assigned a unique Social Security number. This is a one-to-one function because each number corresponds to only one individual.
• Car Identification Numbers (VINs): Each car has a unique VIN. No two cars have the same VIN, making it a one-to-one function.
• Student ID Numbers: In many educational institutions, each student is assigned a unique ID number. This ensures that each student can be uniquely identified.
• Email Addresses: Each email address is unique and assigned to a single user. This allows for distinct communication between individuals.

Understanding these examples can provide a clearer sense of how one-to-one functions operate and where they appear in practical contexts.

2. Horizontal Line Test

The horizontal line test is a visual method used to determine whether a function is one-to-one by examining its graph.

2.1. How the Horizontal Line Test Works

To perform the horizontal line test:

1. Draw the graph of the function f(x) on a coordinate plane.
2. Draw a horizontal line across the graph.
3. If the horizontal line intersects the graph at more than one point at any location, the function is not one-to-one. If the horizontal line never intersects the graph at more than one point, the function is one-to-one.

2.2. Examples of the Horizontal Line Test

Let’s look at some examples:

1. Function: f(x) = x + 2 (Linear Function)

   • When you graph this function, it forms a straight line. No horizontal line will intersect this graph more than once, so it is a one-to-one function.

2. Function: f(x) = x^2 (Quadratic Function)

   • The graph of this function is a parabola. A horizontal line, like y = 4, intersects the graph at x = 2 and x = -2. Because the horizontal line intersects the graph at more than one point, this function is not one-to-one.

3. Function: f(x) = x^3 (Cubic Function)

   • The graph of this function is a curve that continuously increases. Any horizontal line will intersect this graph at only one point, indicating that it is a one-to-one function.

4. Function: f(x) = sin(x) (Sine Function)

   • The sine function oscillates between -1 and 1. A horizontal line between these values will intersect the graph multiple times, indicating that it is not a one-to-one function.

5. Function: f(x) = e^x (Exponential Function)

   • The graph of this function increases continuously and never intersects any horizontal line more than once. Therefore, the exponential function is one-to-one.

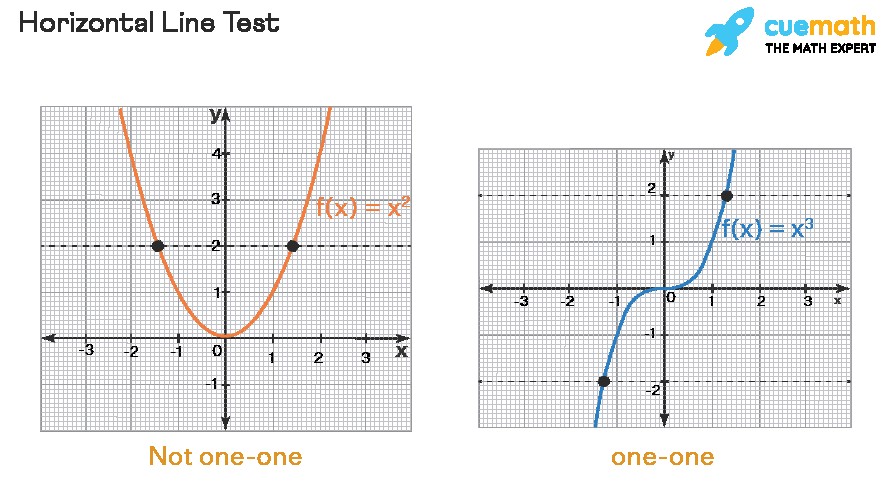
The image illustrates the horizontal line test for a one-to-one function. In this case, the function passes the test because the horizontal line intersects the graph at only one point.

2.3. Why the Horizontal Line Test Works

The horizontal line test is based on the definition of a one-to-one function. If a horizontal line intersects the graph of a function at more than one point, it means there are multiple x values (inputs) that yield the same y value (output). This violates the condition that each element in the range must correspond to a unique element in the domain, and thus the function is not one-to-one.

For example, if the horizontal line y = k intersects the graph at points (x1, k) and (x2, k), it means that f(x1) = k and f(x2) = k. Since x1 ≠ x2, the function is not one-to-one.

3. Properties of One-to-One Functions

One-to-one functions possess several distinct properties that make them useful in various mathematical contexts.

3.1. Key Properties

1. Composition of One-to-One Functions:

   • If two functions, f(x) and g(x), are both one-to-one, their composition (f ◦ g)(x) = f(g(x)) is also one-to-one. This means that if f and g each map distinct inputs to distinct outputs, then applying g first and then f will also result in distinct outputs for distinct inputs.
   • Mathematically: If f(x) and g(x) are one-to-one, then (f ◦ g)(x1) = (f ◦ g)(x2) implies x1 = x2.

2. Inverse Function Existence:

   • A function f(x) has an inverse function f^(-1)(x) if and only if f(x) is one-to-one. The inverse function “undoes” what the original function does, mapping the outputs back to their original inputs.
   • Mathematically: If f(x) is one-to-one, then f^(-1)(f(x)) = x for all x in the domain of f, and f(f^(-1)(x)) = x for all x in the domain of f^(-1).

3. Monotonicity:

   • If a continuous function f(x) is strictly increasing or strictly decreasing over its entire domain, then it is one-to-one. This means the function is either always going up or always going down, ensuring that no two different inputs produce the same output.
   • Mathematically: If f'(x) > 0 for all x (strictly increasing) or f'(x) < 0 for all x (strictly decreasing), then f(x) is one-to-one.

4. Domain and Range of Inverse:

   • The domain of the inverse function f^(-1)(x) is the range of the original function f(x), and the range of f^(-1)(x) is the domain of f(x). This property is crucial when finding and working with inverse functions.
   • Mathematically: Domain(f^(-1)) = Range(f) and Range(f^(-1)) = Domain(f).

5. Symmetry:

   • The graph of a one-to-one function and the graph of its inverse are symmetric with respect to the line y = x. This means if you were to fold the coordinate plane along the line y = x, the graph of f(x) would perfectly overlap the graph of f^(-1)(x).

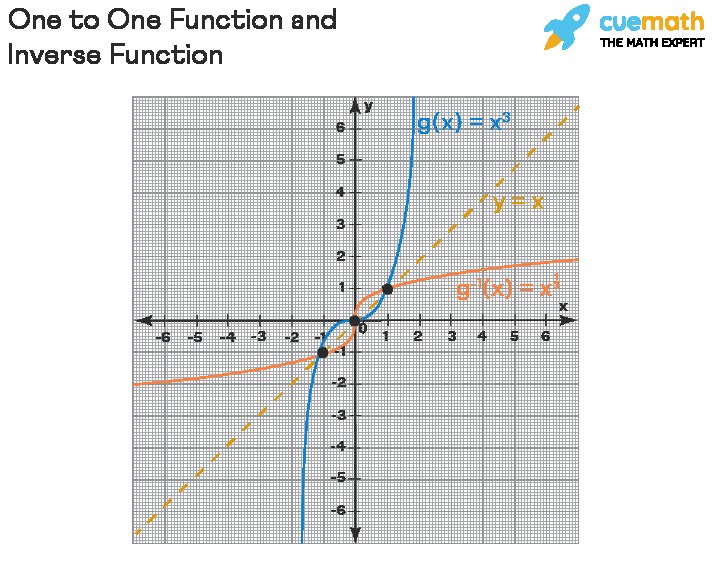
This image illustrates that the graphs of a one-to-one function and its inverse are symmetric with respect to the line y = x. This symmetry highlights the reciprocal relationship between the function and its inverse.

3.2. Practical Implications

• Cryptography: One-to-one functions are used in encryption algorithms to ensure that each input (plaintext) is transformed into a unique output (ciphertext), which can be decrypted back to the original plaintext.
• Data Compression: In some data compression techniques, one-to-one functions are used to map data to a smaller set of values without losing information.
• Database Management: One-to-one relationships are used to ensure that each record in one table corresponds to exactly one record in another table, maintaining data integrity.

4. How to Determine if a Function is One-to-One?

There are several methods to determine whether a function is one-to-one.

4.1. Graphical Method: Horizontal Line Test

As previously discussed, the horizontal line test involves drawing a horizontal line through the graph of the function. If the line intersects the graph at more than one point, the function is not one-to-one. If it intersects at only one point (or not at all), the function is one-to-one.

4.2. Algebraic Method

The algebraic method involves using the definition of a one-to-one function directly.

1. Assume f(x1) = f(x2) for arbitrary x1 and x2 in the domain of f.
2. Show that this assumption implies x1 = x2.
3. If you can prove that f(x1) = f(x2) leads to x1 = x2, then f is one-to-one. If you find a counterexample where f(x1) = f(x2) but x1 ≠ x2, then f is not one-to-one.

Example:

• Determine if f(x) = 3x - 5 is one-to-one.

  • Assume f(x1) = f(x2).
  • Then, 3x1 - 5 = 3x2 - 5.
  • Add 5 to both sides: 3x1 = 3x2.
  • Divide both sides by 3: x1 = x2.
  • Since f(x1) = f(x2) implies x1 = x2, the function f(x) = 3x - 5 is one-to-one.

• Determine if f(x) = x^2 - 4 is one-to-one.

  • Assume f(x1) = f(x2).
  • Then, x1^2 - 4 = x2^2 - 4.
  • Add 4 to both sides: x1^2 = x2^2.
  • Take the square root of both sides: x1 = ±x2.
  • Since x1 can be equal to x2 or -x2, this function is not one-to-one. For instance, f(2) = 0 and f(-2) = 0, so two different inputs produce the same output.

4.3. Using Derivatives

If a function is differentiable, you can use its derivative to determine whether it is one-to-one.

1. Find the derivative f'(x) of the function f(x).
2. If f'(x) > 0 for all x in the domain, then f(x) is strictly increasing and thus one-to-one.
3. If f'(x) < 0 for all x in the domain, then f(x) is strictly decreasing and thus one-to-one.
4. If f'(x) changes sign in the domain, then f(x) is not one-to-one.

Example:

• Determine if f(x) = e^x is one-to-one.

  • Find the derivative: f'(x) = e^x.
  • Since e^x > 0 for all x, f(x) is strictly increasing and thus one-to-one.

• Determine if f(x) = x^3 - 6x^2 + 12x - 8 is one-to-one.

  • Find the derivative: f'(x) = 3x^2 - 12x + 12 = 3(x - 2)^2.
  • Since f'(x) ≥ 0 for all x, and f'(x) = 0 only at x = 2 (a single point), f(x) is strictly increasing and thus one-to-one.

5. One-to-One Function Graph

The graph of a one-to-one function has distinct characteristics that distinguish it from functions that are not one-to-one.

5.1. Visual Characteristics

1. Horizontal Line Test:

   • As previously mentioned, the most straightforward way to identify a one-to-one function graphically is by using the horizontal line test. A function is one-to-one if no horizontal line intersects its graph more than once.

2. Monotonic Behavior:

   • One-to-one functions are often monotonic, meaning they are either strictly increasing or strictly decreasing over their entire domain. A strictly increasing function always moves upward as you move from left to right, while a strictly decreasing function always moves downward.

3. Symmetry:

   • The graph of a one-to-one function and its inverse are symmetric with respect to the line y = x. This symmetry can be observed by reflecting the graph of the function across this line.

5.2. Examples of One-to-One Function Graphs

1. Linear Function: f(x) = x + 1

   • This function forms a straight line on the graph. It passes the horizontal line test because any horizontal line intersects it only once. It is also strictly increasing.

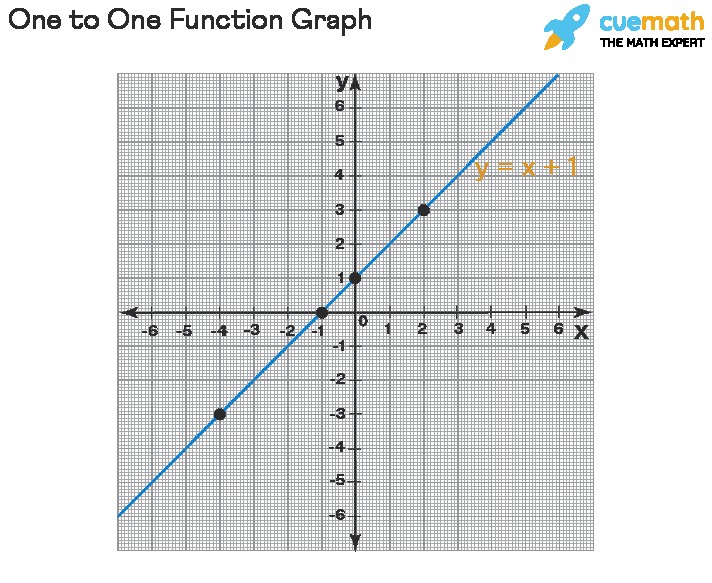
This image shows the graph of the linear function f(x) = x + 1. It passes the horizontal line test, confirming it is a one-to-one function.

2. Exponential Function: f(x) = e^x

   • This function’s graph continuously increases, moving closer to the x-axis as x approaches negative infinity, and increasing rapidly as x becomes positive. It passes the horizontal line test and is strictly increasing.

3. Cubic Function: f(x) = x^3

   • This function’s graph is a curve that continuously increases. Any horizontal line will intersect this graph at only one point, indicating that it is a one-to-one function.

4. Reciprocal Function: f(x) = 1/x

   • The graph consists of two separate curves in the first and third quadrants. Although it has a discontinuity at x = 0, it passes the horizontal line test on each interval of its domain and is therefore one-to-one.

5.3. Non-Examples of One-to-One Function Graphs

1. Quadratic Function: f(x) = x^2

   • The graph of this function is a parabola. It fails the horizontal line test because a horizontal line intersects it at two points, indicating that it is not a one-to-one function.

2. Sine Function: f(x) = sin(x)

   • The sine function oscillates between -1 and 1. A horizontal line between these values will intersect the graph multiple times, indicating that it is not a one-to-one function.

6. Inverse of One-to-One Function

The inverse of a one-to-one function is a function that “undoes” the original function.

6.1. Definition of an Inverse Function

If f(x) is a one-to-one function with domain A and range B, then its inverse function, denoted as f^(-1)(x), has domain B and range A, and it satisfies the following condition:

f^(-1)(f(x)) = x for all x in A

f(f^(-1)(x)) = x for all x in B

In simpler terms, applying the inverse function to the output of the original function gives you back the original input.

6.2. Finding the Inverse of a One-to-One Function

To find the inverse of a one-to-one function f(x):

1. Replace f(x) with y.
2. Swap x and y.
3. Solve for y.
4. Replace y with f^(-1)(x).

Example:

• Find the inverse of f(x) = 2x + 3.

  1. Replace f(x) with y: y = 2x + 3.

  2. Swap x and y: x = 2y + 3.

  3. Solve for y:

     • x - 3 = 2y
     • y = (x - 3) / 2

  4. Replace y with f^(-1)(x): f^(-1)(x) = (x - 3) / 2.

6.3. Properties of Inverse Functions

1. Domain and Range:

   • The domain of f^(-1)(x) is the range of f(x), and the range of f^(-1)(x) is the domain of f(x).

2. Composition:

   • f^(-1)(f(x)) = x for all x in the domain of f(x).
   • f(f^(-1)(x)) = x for all x in the domain of f^(-1)(x).

3. Symmetry:

   • The graphs of f(x) and f^(-1)(x) are symmetric with respect to the line y = x.

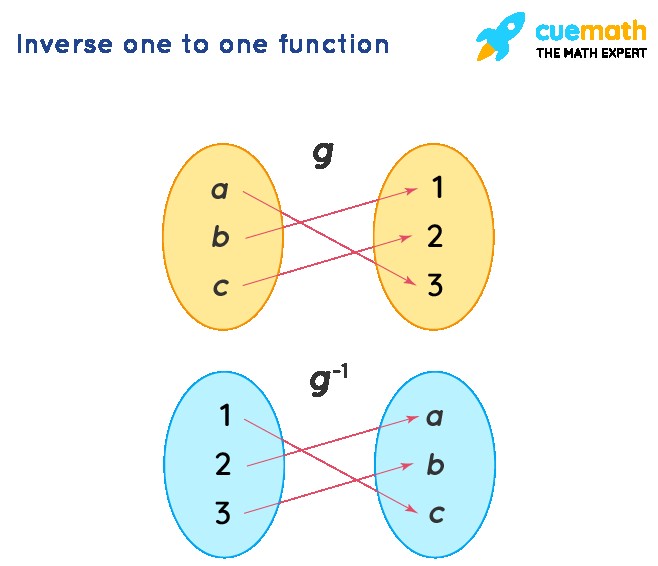
This image illustrates the inverse of a one-to-one function. The ordered pairs of f^(-1) are obtained by interchanging the coordinates in each ordered pair of f.

6.4. Importance of One-to-One Functions for Inverses

A function must be one-to-one to have an inverse. If a function is not one-to-one, different inputs map to the same output, making it impossible to uniquely “undo” the function.

7. Steps to Find the Inverse of One-to-One Function

Finding the inverse of a one-to-one function involves a systematic approach.

7.1. Detailed Steps

1. Replace f(x) with y:

   • Start with the function f(x). Replace f(x) with y to make the equation easier to manipulate.
   • Example: If f(x) = 5x - 2, rewrite it as y = 5x - 2.

2. Swap x and y:

   • Interchange the variables x and y in the equation. This step reflects the function across the line y = x.
   • Example: Swap x and y in y = 5x - 2 to get x = 5y - 2.

3. Solve for y:

   • Rearrange the equation to isolate y on one side. This involves performing algebraic operations to get y by itself.

   • Example: Solve x = 5y - 2 for y:

     • Add 2 to both sides: x + 2 = 5y.
     • Divide by 5: y = (x + 2) / 5.

4. Replace y with f^(-1)(x):

   • Replace y with f^(-1)(x) to denote the inverse function. This is the final form of the inverse function.
   • Example: Replace y with f^(-1)(x) in y = (x + 2) / 5 to get f^(-1)(x) = (x + 2) / 5.

7.2. Example Walkthrough

Let’s find the inverse of the function f(x) = (x - 4) / 3.

1. Replace f(x) with y:

   • y = (x - 4) / 3

2. Swap x and y:

   • x = (y - 4) / 3

3. Solve for y:

   • Multiply both sides by 3: 3x = y - 4.
   • Add 4 to both sides: y = 3x + 4.

4. Replace y with f^(-1)(x):

   • f^(-1)(x) = 3x + 4

7.3. Common Mistakes to Avoid

• Not Swapping x and y: Forgetting to swap x and y is a common mistake. This step is crucial because it reflects the function across the line y = x, which is essential for finding the inverse.
• Incorrectly Solving for y: Make sure to perform algebraic operations correctly to isolate y. Double-check each step to avoid errors.
• Assuming Every Function Has an Inverse: Only one-to-one functions have inverses. If a function is not one-to-one, it does not have an inverse function.
• Confusing f^(-1)(x) with 1 / f(x): The inverse function f^(-1)(x) is not the same as the reciprocal 1 / f(x). The inverse function “undoes” the original function, while the reciprocal is simply the inverse of the function’s value.

8. FAQs on One-to-One Functions

8.1. What is the Definition of One-to-One Function?

A one-to-one function is a function where each element of the range corresponds to exactly one element of the domain. In simpler terms, no two different inputs produce the same output. Mathematically, if f(x1) = f(x2), then x1 = x2. This property ensures that each output is uniquely associated with a specific input.

8.2. What is the Difference Between the Vertical Line Test and the Horizontal Line Test?

The vertical line test and horizontal line test are used to determine different properties of a function.

Feature	Vertical Line Test	Horizontal Line Test
Purpose	Determines if a relation is a function.	Determines if a function is one-to-one (injective).
How it works	A vertical line should intersect the graph at most once for it to be a function.	A horizontal line should intersect the graph at most once for it to be a one-to-one function.
Implication	If the vertical line intersects more than once, the relation is not a function.	If the horizontal line intersects more than once, the function is not one-to-one.
Mathematical Basis	Ensures that each input (x-value) has only one output (y-value).	Ensures that each output (y-value) has only one input (x-value).
Example	y = ±√x fails the vertical line test, hence not a function.	y = x^2 fails the horizontal line test, hence not one-to-one.

8.3. How Do You Check if a Function is One-to-One?

You can check if a function is one-to-one using several methods:

• Graphical Method (Horizontal Line Test): Draw the graph of the function and check if any horizontal line intersects the graph more than once. If it does, the function is not one-to-one.
• Algebraic Method: Assume f(x1) = f(x2) and show that this implies x1 = x2. If you can prove this, the function is one-to-one. If you find a counterexample where f(x1) = f(x2) but x1 ≠ x2, the function is not one-to-one.
• Using Derivatives: If the function is differentiable, find its derivative f'(x). If f'(x) > 0 for all x in the domain, the function is strictly increasing and one-to-one. If f'(x) < 0 for all x in the domain, the function is strictly decreasing and one-to-one.

8.4. What Types of Functions Are One-to-One Functions?

Certain types of functions are commonly one-to-one:

• Linear Functions: f(x) = mx + b, where m ≠ 0.
• Exponential Functions: f(x) = a^x, where a > 0 and a ≠ 1.
• Logarithmic Functions: f(x) = log_a(x), where a > 0 and a ≠ 1.
• Strictly Monotonic Functions: Functions that are either strictly increasing or strictly decreasing over their entire domain.

8.5. What Does It Mean if a Function is Not One-to-One?

If a function is not one-to-one, it means that there exist at least two different inputs that produce the same output. Mathematically, this means there exist x1 and x2 such that x1 ≠ x2, but f(x1) = f(x2). Such functions are called many-to-one functions. An example is the quadratic function f(x) = x^2, where f(2) = 4 and f(-2) = 4.

8.6. What Are the Steps in Solving the Inverse of a One-to-One Function?

The steps to find the inverse of a one-to-one function f(x) are as follows:

1. Replace f(x) with y.
2. Swap x and y.
3. Solve for y in terms of x.
4. Replace y with f^(-1)(x) to denote the inverse function.

8.7. What is an Example of a One-to-One Function?

The linear function f(x) = 3x + 2 is a one-to-one function. To prove this, assume f(x1) = f(x2):

3x1 + 2 = 3x2 + 2

Subtract 2 from both sides:

3x1 = 3x2

Divide by 3:

x1 = x2

Since f(x1) = f(x2) implies x1 = x2, the function is one-to-one.

8.8. What is Not a One-to-One Function?

The quadratic function f(x) = x^2 is not a one-to-one function. For example, f(3) = 9 and f(-3) = 9. Here, two different inputs, 3 and -3, produce the same output, 9, violating the one-to-one condition.

8.9. Are Parabolas One-to-One Functions?

No, parabolas are generally not one-to-one functions. A parabola is the graph of a quadratic function, and quadratic functions have the form f(x) = ax^2 + bx + c, where a ≠ 0. These functions are symmetric about their vertex, meaning that for any x value, there is another x value that produces the same output. Therefore, parabolas fail the horizontal line test.

8.10. How Can We Apply the Concept of One-to-One Functions in Daily Life?

One-to-one functions are applicable in various real-life scenarios:

• Unique Identification: Social Security numbers, student IDs, and car VINs are all examples of one-to-one functions, where each number uniquely identifies an individual or object.
• Cryptography: Encryption algorithms use one-to-one functions to ensure that each plaintext message is converted to a unique ciphertext message, which can be decrypted back to the original.
• Database Management: In database systems, one-to-one relationships ensure that each record in one table corresponds to exactly one record in another table, maintaining data integrity.
• Matching problems: One-to-one functions can be used to solve matching problems, such as assigning students to dorm rooms or matching job applicants with available positions.

Do you still have burning questions about one-to-one functions? At WHAT.EDU.VN, we understand the challenges of finding quick and reliable answers. That’s why we offer a free platform to ask any question and receive expert responses. No matter how simple or complex your query, WHAT.EDU.VN is here to help. Visit WHAT.EDU.VN today at 888 Question City Plaza, Seattle, WA 98101, United States, or reach out via WhatsApp at +1 (206) 555-7890 to experience the ease of getting your questions answered!