Are you curious about perpendicular lines and their significance in geometry and everyday life? At WHAT.EDU.VN, we provide clear explanations. A perpendicular line is formed when two lines intersect at a right angle (90 degrees). This article delves into the definition, properties, and real-world examples of perpendicular lines, providing you with a comprehensive understanding of this fundamental geometric concept. Let’s explore perpendicularity, right angles, and intersecting lines together.
1. Defining Perpendicular Lines: What Are They?
Perpendicular lines are defined as two lines that intersect at a right angle (90 degrees). In simpler terms, imagine two straight lines crossing each other perfectly to form a corner that looks exactly like the corner of a square or a book. That’s a perpendicular intersection. This concept is fundamental in geometry and has numerous applications in real life.
To understand this better, let’s break down the key components:
- Lines: A line is a straight, one-dimensional figure extending infinitely in both directions.
- Intersection: This is the point where two lines meet or cross each other.
- Right Angle: A right angle is an angle that measures exactly 90 degrees. It is often denoted by a small square at the corner where the lines meet.
Therefore, when these elements come together—two lines intersecting to form a right angle—we have perpendicular lines.
The term “perpendicular” comes from the Latin word “perpendicularis,” which means “plumb line.” A plumb line is a vertical line used to determine if something is perfectly upright, emphasizing the right angle aspect.
Consider lines AB and CD intersecting at point E. If the angle formed at point E is 90 degrees, then AB is perpendicular to CD, and vice versa. This relationship is often denoted as AB ⊥ CD, where the symbol “⊥” indicates perpendicularity.
2. The Significance of a 90-Degree Angle in Perpendicularity
The essence of perpendicularity lies in the 90-degree angle formed at the point of intersection. This right angle is what distinguishes perpendicular lines from other intersecting lines. When two lines intersect at any angle other than 90 degrees, they are simply called intersecting lines, but not perpendicular lines.
- Importance of Precision: In fields like construction and engineering, ensuring lines are perfectly perpendicular is critical. A slight deviation from 90 degrees can lead to structural weaknesses or misalignments.
- Mathematical Foundation: The 90-degree angle is a cornerstone of many geometric theorems and proofs. It simplifies calculations and provides a reliable reference point.
- Everyday Applications: From the corners of buildings to the way streets are laid out in a grid, the right angle is a ubiquitous feature of our built environment.
3. The Symbol for Perpendicular Lines: ⊥
The symbol “⊥” is universally used to denote perpendicularity. This symbol is placed between the names of the two lines that are perpendicular to each other. For example, if line AB is perpendicular to line CD, it is written as AB ⊥ CD.
Using this symbol provides a concise and clear way to indicate the relationship between two lines without having to write out the full sentence.
Practical Examples of the Perpendicular Symbol
- Mathematical Equations: In geometric proofs and equations, the ⊥ symbol helps quickly convey the relationship between different lines and segments.
- Diagrams and Drawings: In technical drawings, architects and engineers use the ⊥ symbol to label perpendicular elements, ensuring accuracy and clarity.
- Educational Materials: Textbooks and online resources use the ⊥ symbol to teach students about geometric concepts and notation.
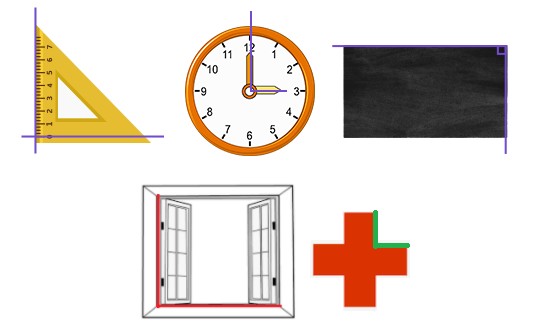
4. Real-World Examples of Perpendicular Lines
Perpendicular lines are not just abstract geometric concepts; they are all around us in everyday life. Recognizing them in the real world can help solidify your understanding.
Common Examples
- Building Corners: The corners of most buildings, rooms, and furniture are designed with perpendicular lines to provide stability and structure.
- Window Panes: The lines that make up window panes are typically perpendicular to each other, creating a grid-like pattern.
- Crossroads: Many road intersections are designed with perpendicular streets, facilitating orderly traffic flow.
- Clock Hands at 3:00: At exactly 3:00, the hour and minute hands of an analog clock form a 90-degree angle.
- Set Squares: The sides of a set square, a tool used in technical drawing, are designed to be perfectly perpendicular.
Detailed Examples
- Construction: In building construction, ensuring that walls are perpendicular to the floor is essential for stability. Plumb lines and levels are used to achieve this accuracy.
- Gardening: When creating garden beds or laying out pathways, gardeners often use perpendicular lines to create neat, orderly designs.
- Sports: On a sports field, the lines marking the boundaries are often perpendicular to each other, defining the playing area.
5. Properties of Perpendicular Lines
Perpendicular lines exhibit several unique properties that are important to understand for various applications in geometry and beyond.
Key Properties
- Right Angle Formation: Perpendicular lines always intersect at a 90-degree angle. This is the defining characteristic.
- Shortest Distance: The shortest distance from a point to a line is along the perpendicular line connecting the point to the line.
- Parallelism: If two lines are perpendicular to the same line, they are parallel to each other. This is a useful property in many geometric proofs.
- Slope Relationship: In coordinate geometry, if two lines are perpendicular, the product of their slopes is -1 (except when one line is vertical).
- Unique Perpendicular: Through a given point on a line, there is only one line that can be drawn perpendicular to the given line.
Elaboration on Properties
- Slope Relationship: The slope of a line measures its steepness. If one line has a slope of m, a line perpendicular to it will have a slope of -1/m. For instance, if a line has a slope of 2, a perpendicular line will have a slope of -1/2.
- Parallelism: Imagine three lines: A, B, and C. If line A is perpendicular to line B, and line C is also perpendicular to line B, then lines A and C are parallel to each other. This property is often used in architectural and engineering designs.
6. Perpendicular Lines vs. Parallel Lines: What’s the Difference?
It’s easy to confuse perpendicular and parallel lines, but they have distinct characteristics. Understanding these differences is crucial for mastering geometry.
Comparison Table
| Feature | Perpendicular Lines | Parallel Lines |
|---|---|---|
| Definition | Intersect at a 90-degree angle | Never intersect; always equidistant |
| Angle of Intersection | 90 degrees | 0 degrees (or 180 degrees, depending on the definition) |
| Symbol | ⊥ | |
| Intersection | Always intersect at one point | Never intersect |
| Real-life Examples | Corners of a square, intersecting streets | Railway tracks, edges of a ruler |

Detailed Comparison
- Intersection: Perpendicular lines always intersect, while parallel lines never do. This is the most fundamental difference.
- Angle: The angle between perpendicular lines is always 90 degrees, while the angle between parallel lines is 0 degrees (they run in the same direction) or 180 degrees (they run in opposite directions but remain equidistant).
- Symbol: The symbol ⊥ denotes perpendicularity, while || denotes parallelism.
- Slope: In coordinate geometry, perpendicular lines have slopes that are negative reciprocals of each other, while parallel lines have the same slope.
7. How to Construct Perpendicular Lines
Constructing perpendicular lines accurately is a valuable skill in both mathematics and practical applications. There are two primary methods: using a protractor and using a compass and straightedge.
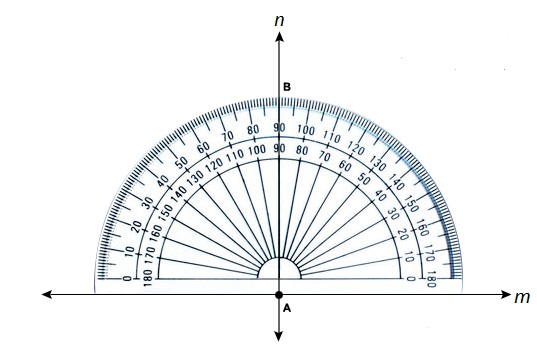
Method 1: Using a Protractor
A protractor is a tool used to measure angles. It can be used to create accurate perpendicular lines.
Steps:
- Draw a Line: Start by drawing a straight line using a ruler. Label this line m.
- Mark a Point: Choose a point on the line where you want to draw the perpendicular line. Label this point A.
- Place the Protractor: Place the protractor on the line m such that its base lines coincides with m, and its center falls on A.
- Find 90 Degrees: Locate the 90-degree mark on the protractor.
- Mark the Point: Make a dot at the 90-degree mark. Label this point B.
- Draw the Perpendicular Line: Use the ruler to draw a line from point A through point B. This line, n, is perpendicular to line m at point A.
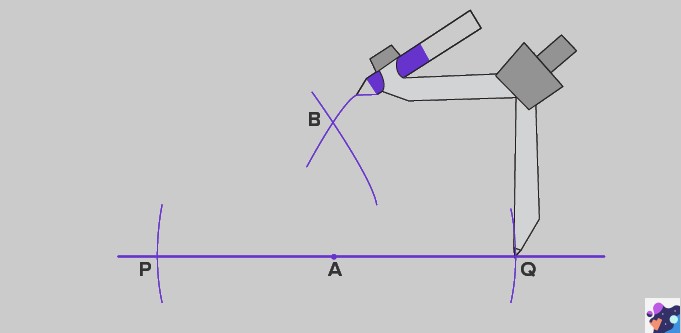
Method 2: Using a Compass and Straightedge
A compass and straightedge (ruler without measurements) can also be used to construct perpendicular lines.
Steps:
- Draw a Line: Begin by drawing a straight line using a straightedge. Label this line m.
- Mark a Point: Choose a point on the line where you want to draw the perpendicular line. Label this point A.
- Set the Compass: Place the compass tip on point A. Open the compass to an appropriate radius.
- Draw Arcs: Draw an arc on either side of point A, intersecting line m. Label these intersection points C and D.
- Increase Compass Radius: Stretch the compass wider. Place the compass tip on point C and draw an arc above line m.
- Draw Intersecting Arc: Without changing the compass radius, place the compass tip on point D and draw another arc above line m. These two arcs will intersect. Label the intersection point B.
- Draw the Perpendicular Line: Use the straightedge to draw a line from point A through point B. This line, n, is perpendicular to line m at point A.
8. Examples of Perpendicular Lines in Geometric Shapes
Perpendicular lines are fundamental in various geometric shapes. Recognizing them helps in understanding the properties and characteristics of these shapes.
Squares and Rectangles
In squares and rectangles, all adjacent sides are perpendicular to each other. This means that each corner forms a perfect right angle.
- Square: A square has four equal sides, and all four angles are right angles. Therefore, every pair of adjacent sides is perpendicular.
- Rectangle: A rectangle has opposite sides that are equal in length, and all four angles are right angles. Like the square, every pair of adjacent sides is perpendicular.
Right Triangles
A right triangle is a triangle that has one angle measuring 90 degrees. The two sides that form the right angle are perpendicular to each other.
- Legs: The two sides that form the right angle are called legs. These legs are, by definition, perpendicular to each other.
- Hypotenuse: The side opposite the right angle is called the hypotenuse. It is the longest side of the right triangle.
Other Shapes
- Kites and Rhombuses: The diagonals of a kite and a rhombus intersect at right angles, making them perpendicular.
- Trapezoids: In a right trapezoid, at least one of the non-parallel sides is perpendicular to the parallel sides.
9. Solved Examples: Identifying Perpendicular Lines
To solidify your understanding, let’s go through some solved examples to help you identify perpendicular lines in various scenarios.
Example 1: Identifying Perpendicular Lines in a Diagram
Question: Identify the perpendicular lines in the following diagram.
Solution:
By examining the diagram, we can see that:
- Line AB is perpendicular to line CD.
- Line EF is parallel to line GH.
Example 2: Determining Perpendicularity in Real-World Objects
Question: Are the edges of a rectangular table perpendicular to each other?
Solution:
Yes, the edges of a rectangular table are perpendicular to each other because a rectangle is defined as having four right angles at its corners.
Example 3: Calculating Slopes to Determine Perpendicularity
Question: Line L1 has a slope of 2. Line L2 has a slope of -1/2. Are L1 and L2 perpendicular?
Solution:
To determine if the lines are perpendicular, multiply their slopes:
2 * (-1/2) = -1
Since the product of the slopes is -1, the lines L1 and L2 are perpendicular.
10. Practice Problems: Test Your Knowledge
Now it’s your turn to test your understanding of perpendicular lines. Try these practice problems:
- Identify the perpendicular line segments in a given shape.
- Each object has a highlighted pair of lines. Which of this object highlighted pair of lines does not show perpendicular lines?
- At what time the hands of the clock will be perpendicular to each other?
- How many lines are perpendicular to line CD in a given figure?
- At what time will the hands of the clock be perpendicular?
- Perpendicular lines intersect each other at ___ angle.
- In which of the following objects can we find perpendicular lines?
[ Image of Practice problems related to perpendicular lines ]
Answers:
- FE and ED
- A
- 3 o’clock
- 3
- 9:00 am
- Right
- Laptop
11. Why Understanding Perpendicular Lines Matters
Understanding perpendicular lines is crucial for several reasons, impacting various fields and daily activities.
Practical Applications
- Construction and Architecture: Ensuring that walls are perpendicular to the ground is essential for structural integrity. Architects and engineers rely on precise perpendicularity for building design and stability.
- Navigation: Maps and navigation systems use grid systems based on perpendicular lines to accurately represent locations and directions.
- Manufacturing: In manufacturing, creating parts with precise right angles is critical for assembly and functionality.
- Computer Graphics: Perpendicularity is used in computer graphics for rendering images, creating 3D models, and ensuring accurate perspectives.
Educational Benefits
- Geometry: Understanding perpendicular lines is a fundamental concept in geometry, providing a foundation for more advanced topics such as trigonometry and calculus.
- Problem Solving: Recognizing and working with perpendicular lines helps develop critical thinking and problem-solving skills.
- Spatial Reasoning: Learning about perpendicular lines enhances spatial reasoning abilities, which are important for fields like architecture, engineering, and design.
12. Frequently Asked Questions (FAQs) About Perpendicular Lines
To further clarify any remaining questions, here are some frequently asked questions about perpendicular lines.
Common Questions
Q: What are perpendicular lines?
A: Perpendicular lines are two lines that intersect at a right angle (90 degrees).
Q: Do perpendicular lines have to meet?
A: Yes, perpendicular lines must intersect at a point to form a right angle.
Q: What is the perpendicular symbol?
A: The symbol used to denote perpendicularity is ⊥.
Q: What is the difference between perpendicular lines and parallel lines?
A: Perpendicular lines intersect at a 90-degree angle, while parallel lines never intersect and remain equidistant from each other.
Q: Are all intersecting lines always perpendicular?
A: No, not all intersecting lines are perpendicular. They must intersect at a 90-degree angle to be considered perpendicular.
Q: Is it possible to have two lines that are both parallel and perpendicular to each other?
A: No, it is not possible. Parallel lines never intersect, while perpendicular lines always intersect at a right angle.
Q: How many perpendicular lines can be drawn to a given line passing through a given point on a line?
A: Only one perpendicular line can be drawn to a given line through a specific point on that line.
Q: How many perpendicular lines can be drawn to a given line?
A: An infinite number of perpendicular lines can be drawn to a given line, each passing through a different point on the line.
13. Advanced Concepts Related to Perpendicular Lines
Once you have a solid understanding of the basics, you can explore more advanced concepts related to perpendicular lines.
Perpendicular Bisectors
A perpendicular bisector is a line that intersects a line segment at its midpoint and is perpendicular to it. This concept is crucial in geometry for constructions and proofs.
- Properties: A perpendicular bisector divides a line segment into two equal parts and forms a 90-degree angle with the segment.
- Applications: Perpendicular bisectors are used in constructing geometric shapes, finding the center of a circle, and solving geometric problems.
Orthogonal Projections
An orthogonal projection is a way of projecting a point or shape onto a line or plane such that the projection lines are perpendicular to the line or plane.
- Applications: Orthogonal projections are used in engineering, architecture, and computer graphics to create accurate representations of objects and structures.
Normal Vectors
In three-dimensional space, a normal vector is a vector that is perpendicular to a surface at a given point.
- Applications: Normal vectors are used in computer graphics, physics, and engineering to calculate lighting, forces, and surface interactions.
14. Tips for Teaching and Learning About Perpendicular Lines
Teaching and learning about perpendicular lines can be made easier with the right strategies and resources.
Tips for Teachers
- Use Visual Aids: Use diagrams, models, and real-world examples to illustrate the concept of perpendicular lines.
- Hands-On Activities: Engage students in hands-on activities such as constructing perpendicular lines using protractors and compasses.
- Real-World Connections: Connect the concept of perpendicular lines to real-world applications in architecture, engineering, and design.
- Interactive Tools: Utilize interactive online tools and simulations to help students visualize and manipulate perpendicular lines.
Tips for Learners
- Practice Regularly: Practice drawing and identifying perpendicular lines to reinforce your understanding.
- Use Real-World Examples: Look for examples of perpendicular lines in your environment to make the concept more relatable.
- Ask Questions: Don’t hesitate to ask questions if you’re unsure about any aspect of perpendicular lines.
- Online Resources: Utilize online resources such as videos, tutorials, and practice problems to supplement your learning.
15. Conclusion: Mastering the Concept of Perpendicular Lines
Understanding perpendicular lines is a cornerstone of geometry and has far-reaching applications in various fields. By grasping the definition, properties, and real-world examples, you can enhance your problem-solving skills and spatial reasoning abilities. Whether you are a student, teacher, or professional, a solid understanding of perpendicular lines is invaluable.
Have more questions about perpendicular lines or other geometric concepts? Visit WHAT.EDU.VN, where you can ask questions and receive free answers from experts. We are here to help you navigate the world of mathematics with ease and confidence. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States, or reach out via WhatsApp at +1 (206) 555-7890. Explore what.edu.vn today and unlock your full learning potential!
