What Is a Quotient in Math? Understanding Division Results

Are you struggling to understand what a quotient is in math? WHAT.EDU.VN is here to help you grasp this fundamental concept. A quotient represents the result you get when you divide one number by another, a key component in division problems. Let’s explore the world of quotients, division, and how it all fits together, including remainders and factors. Ready to unlock the secrets of division?

1. What is a Quotient in Math?

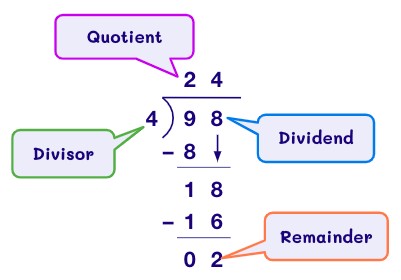
In mathematics, the quotient is the result obtained from dividing one number by another. It represents how many times one number (the divisor) fits into another number (the dividend). Think of it as the “answer” to a division problem.

For example, in the equation 10 ÷ 2 = 5, the quotient is 5. This means that 2 fits into 10 five times. The quotient, division, remainder, dividend and divisor are all crucial parts of mathematical equations.

2. Understanding the Components of a Division Problem

To fully grasp the concept of a quotient, it’s essential to understand the other parts of a division problem:

Dividend: The number being divided (the total amount).
Divisor: The number by which the dividend is divided (the number of groups or the size of each group).
Quotient: The result of the division (how many items are in each group or how many groups there are).
Remainder: The amount left over when the dividend cannot be divided evenly by the divisor.

Here’s a simple analogy: Imagine you have 15 cookies (the dividend) and want to share them equally among 4 friends (the divisor). Each friend would get 3 cookies (the quotient), and you would have 3 cookies left over (the remainder).

3. Quotient Examples

Let’s look at a few examples to solidify your understanding:

Example 1: 20 ÷ 4 = 5
- Dividend: 20
- Divisor: 4
- Quotient: 5 (4 fits into 20 five times)
- Remainder: 0 (no leftover)
Example 2: 25 ÷ 6 = 4 R 1
- Dividend: 25
- Divisor: 6
- Quotient: 4 (6 fits into 25 four times)
- Remainder: 1 (1 leftover)
Example 3: 36 ÷ 9 = 4
- Dividend: 36
- Divisor: 9
- Quotient: 4 (9 fits into 36 four times)
- Remainder: 0 (no leftover)

4. Types of Quotients: Whole Numbers and Decimals

The quotient can be either a whole number or a decimal number, depending on whether the dividend is perfectly divisible by the divisor.

Whole Number Quotient: When the dividend is completely divisible by the divisor, the quotient is a whole number. This means there is no remainder.
- Example: 12 ÷ 3 = 4 (whole number)
Decimal Quotient: When the dividend is not completely divisible by the divisor, the quotient is a decimal number. This means there is a remainder, which can be expressed as a decimal.
- Example: 13 ÷ 2 = 6.5 (decimal number)

5. Finding the Quotient Using Different Methods

There are several methods to find the quotient, including:

5.1. Repeated Subtraction

Repeated subtraction involves subtracting the divisor from the dividend until you reach zero or a number smaller than the divisor. The number of times you subtract is the quotient.

Example: Find the quotient of 15 ÷ 3 using repeated subtraction.

15 – 3 = 12
12 – 3 = 9
9 – 3 = 6
6 – 3 = 3
3 – 3 = 0

We subtracted 3 five times to reach 0, so the quotient is 5.

5.2. Long Division

Long division is a standard algorithm for dividing larger numbers. It involves a series of steps: divide, multiply, subtract, bring down, and repeat.

Example: Find the quotient of 156 ÷ 12 using long division.

    13
  --------
12|  156
   - 12
   ------
     36
   - 36
   ------
      0

The quotient is 13.

5.3. Using a Calculator

For quick calculations, a calculator is a convenient tool. Simply enter the dividend, press the division symbol, enter the divisor, and press the equals button to find the quotient.

Example: To find the quotient of 247 ÷ 19, enter 247 ÷ 19 into a calculator. The result is 13.

6. The Relationship Between Quotient, Divisor, and Dividend

The quotient, divisor, and dividend are interconnected. The fundamental relationship is:

Dividend = Divisor × Quotient + Remainder

This equation can be used to check the accuracy of a division problem.

Example: 27 ÷ 4 = 6 R 3

Dividend: 27
Divisor: 4
Quotient: 6
Remainder: 3

Check: 4 × 6 + 3 = 24 + 3 = 27 (which is the dividend)

7. Real-World Applications of Quotients

Quotients are used in many real-world situations, including:

Sharing: Dividing a quantity of items equally among a group of people.
Measurement: Determining how many times a smaller unit fits into a larger unit.
Cooking: Adjusting recipes to serve a different number of people.
Finance: Calculating unit prices or dividing expenses.

8. Why is Understanding Quotients Important?

Understanding quotients is crucial because division is a fundamental mathematical operation used in various aspects of life. It helps in problem-solving, critical thinking, and decision-making.

9. Common Mistakes to Avoid When Finding Quotients

Incorrectly Placing the Numbers: Ensure you place the dividend and divisor in the correct positions in long division.
Forgetting the Remainder: Always account for the remainder, especially in real-world problems.
Misinterpreting the Question: Understand what the question is asking before performing the division.

10. Let WHAT.EDU.VN Help You Master Quotients and More

At WHAT.EDU.VN, we understand that math can sometimes be challenging. If you’re struggling with quotients, division, or any other math concept, don’t hesitate to ask us your questions. Our team of experts is here to provide clear, concise, and helpful answers to guide you on your learning journey.

Long Division Example

11. Exploring the Concept of Remainder in Division

The remainder is a crucial part of understanding division, particularly when the dividend is not perfectly divisible by the divisor. It represents the amount “left over” after performing the division. Understanding remainders helps in various real-world applications, such as dividing resources or understanding cyclical patterns.

For example, if you have 23 apples and want to divide them equally among 5 friends, each friend would get 4 apples, and you would have 3 apples left over. In this case, 4 is the quotient, and 3 is the remainder.

12. How to Interpret Remainders in Real-World Contexts

Interpreting remainders correctly is essential for applying division in practical scenarios. Here are some examples:

Dividing Students into Groups: If a teacher has 35 students and wants to divide them into groups of 8, there will be 4 groups (quotient) and 3 students left over (remainder). This means there will be 4 full groups, and one group with only 3 students.
Scheduling Tasks: If a task takes 7 hours to complete and you have 24 hours, you can complete the task 3 times (quotient) with 3 hours remaining (remainder). This remaining time can be used for other activities.
Distributing Resources: If you have 50 pencils to distribute among 9 children, each child will receive 5 pencils (quotient), and there will be 5 pencils left over (remainder). You can decide to give these extra pencils to specific children or keep them for later use.

13. Using Quotients to Solve Word Problems

Word problems often require applying division to find a solution. Understanding how to identify the dividend, divisor, and what the question is asking for is key.

Here’s an example:

Problem: A bakery makes 144 cupcakes each day. If they package the cupcakes into boxes of 12, how many boxes do they need each day?

Solution:

Dividend: 144 (total cupcakes)
Divisor: 12 (cupcakes per box)
Quotient: 144 ÷ 12 = 12

The bakery needs 12 boxes each day.

14. Common Division Terminology and Their Meanings

Familiarizing yourself with division terminology can make understanding and solving problems easier. Here are some key terms:

Dividend: The number being divided.
Divisor: The number by which the dividend is divided.
Quotient: The result of the division.
Remainder: The amount left over after division.
Division Symbol (÷): The symbol used to indicate division.
Long Division: A method for dividing larger numbers.
Factors: Numbers that divide evenly into another number with no remainder.
Multiple: The product of a number and any other whole number.

15. Division with Fractions and Decimals

Division can also involve fractions and decimals, which might seem tricky at first but follow the same principles.

15.1. Dividing with Fractions

To divide by a fraction, you multiply by its reciprocal (flipping the numerator and denominator).

Example: 4 ÷ (1/2) = 4 × (2/1) = 8

15.2. Dividing with Decimals

Dividing with decimals involves adjusting the numbers to work with whole numbers, especially in long division.

Example: 12.5 ÷ 0.5 can be rewritten as 125 ÷ 5 = 25

16. Exploring Division with Negative Numbers

Division also applies to negative numbers, which follow specific rules:

A positive number divided by a positive number yields a positive quotient.
A negative number divided by a negative number yields a positive quotient.
A positive number divided by a negative number yields a negative quotient.
A negative number divided by a positive number yields a negative quotient.

Examples:

10 ÷ 2 = 5
(-10) ÷ (-2) = 5
10 ÷ (-2) = -5
(-10) ÷ 2 = -5

17. Understanding the Role of Division in Algebra

Division is an essential operation in algebra and is used to solve equations, simplify expressions, and understand relationships between variables.

17.1. Solving Equations

Division is used to isolate variables in equations. For example, to solve the equation 3x = 15, you would divide both sides by 3:

x = 15 ÷ 3 = 5

17.2. Simplifying Expressions

Division can simplify algebraic expressions by canceling out common factors.

For example, the expression (6x) / 2 can be simplified to 3x by dividing 6 by 2.

17.3. Analyzing Ratios and Proportions

Division is fundamental to understanding ratios and proportions, which are used to compare quantities.

For example, if the ratio of apples to oranges is 2:1, this means that for every 2 apples, there is 1 orange. This ratio can be expressed as a fraction (2/1), which can be used in division problems.

18. How to Estimate Quotients

Estimating quotients is a useful skill for quickly approximating the result of a division problem without performing the exact calculation. This can be helpful for checking if your final answer is reasonable.

Steps to Estimate:

Round the Dividend and Divisor: Round the numbers to the nearest ten, hundred, or thousand to make the division easier.
Perform the Division: Divide the rounded numbers.
Adjust if Necessary: If you rounded significantly, adjust your estimate to get closer to the actual quotient.

Example: Estimate the quotient of 257 ÷ 12.

Round 257 to 260 and 12 to 10.
Divide the rounded numbers: 260 ÷ 10 = 26.
The estimated quotient is 26. The actual quotient is approximately 21.4, so the estimate is reasonably close.

19. Division as the Inverse of Multiplication

Division and multiplication are inverse operations, meaning that one undoes the other. This relationship is essential for understanding and verifying division problems.

Example:

Multiplication: 5 × 3 = 15
Division: 15 ÷ 3 = 5

Understanding this relationship helps in problem-solving and checking the accuracy of calculations.

20. Practice Problems to Strengthen Your Understanding

To solidify your understanding of quotients and division, try solving these practice problems:

Divide 48 by 6.
What is the quotient of 75 divided by 5?
If 220 candies are distributed among 20 children, how many candies does each child get?
A farmer harvests 560 apples and packs them into boxes of 35. How many boxes does he need?
Calculate 16.8 ÷ 2.
What is -36 ÷ 4?

21. Tips for Improving Your Division Skills

Memorize Basic Division Facts: Knowing basic division facts (e.g., 12 ÷ 3 = 4) can speed up calculations.
Practice Regularly: Consistent practice helps build confidence and improves accuracy.
Use Real-World Examples: Applying division to real-world problems makes the concept more relatable and understandable.
Break Down Complex Problems: Divide complex problems into smaller, more manageable steps.
Check Your Work: Always verify your answers using multiplication or estimation.

22. Advanced Division Techniques

As you progress in mathematics, you’ll encounter more advanced division techniques, such as polynomial division and synthetic division, which are used in algebra and calculus.

22.1. Polynomial Division

Polynomial division is used to divide one polynomial by another. It is similar to long division with numbers but involves algebraic expressions.

22.2. Synthetic Division

Synthetic division is a simplified method for dividing a polynomial by a linear factor. It is quicker and easier to use than polynomial division in certain cases.

23. Division in Computer Science and Programming

Division is also a fundamental operation in computer science and programming. It is used in various applications, such as:

Data Analysis: Dividing data sets to calculate averages, percentages, and ratios.
Image Processing: Dividing pixel values to adjust brightness and contrast.
Game Development: Dividing game elements to calculate positions, speeds, and scores.
Financial Calculations: Dividing financial data to perform calculations related to interest, taxes, and investments.

24. Frequently Asked Questions About Quotients

Q: What is the difference between a quotient and a product?

A: A quotient is the result of dividing two numbers, while a product is the result of multiplying two numbers.

Q: How can I check my division answer?

A: You can check your division answer by multiplying the quotient by the divisor and adding the remainder. The result should be the dividend.

Q: What does it mean when the remainder is zero?

A: When the remainder is zero, it means that the dividend is perfectly divisible by the divisor, and the quotient is a whole number.

Q: Can the quotient be a fraction?

A: Yes, the quotient can be a fraction, especially when dividing by a number that does not divide evenly into the dividend.

Q: How is division used in daily life?

A: Division is used in many daily life situations, such as sharing items, calculating unit prices, adjusting recipes, and managing finances.

25. Learn More and Ask Questions at WHAT.EDU.VN

Do you have more questions about quotients, division, or any other math topics? Visit WHAT.EDU.VN to ask your questions and receive free, expert answers. Our website is dedicated to providing clear and helpful explanations to learners of all ages and backgrounds. We believe that everyone can succeed in math with the right resources and support.

26. The Importance of Understanding Division in Financial Literacy

Understanding division is crucial for financial literacy. Whether you’re splitting bills with roommates, calculating the cost per unit when grocery shopping, or figuring out interest rates on loans, division is a key component. A solid grasp of division can help you make informed financial decisions, budget effectively, and manage your money wisely. It’s also invaluable in business, where you need to calculate profits, losses, and other financial metrics.

27. How Division Relates to Other Math Concepts

Division doesn’t exist in isolation; it’s interconnected with many other mathematical concepts.

27.1. Fractions, Decimals, and Percentages

Division is closely tied to fractions, decimals, and percentages. A fraction is essentially a division problem waiting to happen (e.g., 1/2 is the same as 1 ÷ 2). Converting fractions to decimals involves division. Percentages are also related, as they involve dividing a part by the whole and multiplying by 100.

27.2. Ratios and Proportions

Division helps in simplifying ratios and solving proportions. Ratios compare two quantities, and proportions state that two ratios are equal. Division is used to find the simplest form of a ratio and to solve for unknown quantities in a proportion.

27.3. Algebra

As mentioned earlier, division is vital in algebra. It’s used to solve equations, simplify expressions, and understand functions. Without a solid understanding of division, algebraic concepts can be challenging to grasp.

28. Fun Facts About Division

Zero divided by any non-zero number is always zero. However, dividing any number by zero is undefined.
The division symbol (÷) is called an obelus.
Division is one of the four basic operations of arithmetic, along with addition, subtraction, and multiplication.
Ancient civilizations, such as the Egyptians and Babylonians, had their own methods of performing division.

29. Advanced Applications of Division in Science and Engineering

Beyond everyday math, division is used extensively in science and engineering.

29.1. Physics

In physics, division is used to calculate speed (distance divided by time), density (mass divided by volume), and many other fundamental quantities. Understanding division is crucial for solving physics problems and analyzing data.

29.2. Engineering

Engineers use division in various calculations, such as determining the load-bearing capacity of structures, designing circuits, and optimizing processes.

29.3. Chemistry

Chemists use division to calculate concentrations, molar masses, and reaction rates.

30. Why WHAT.EDU.VN is Your Go-To Resource for Math Help

WHAT.EDU.VN is committed to providing accessible, easy-to-understand explanations for all your math questions. Our platform offers:

Free Answers: Get your math questions answered for free by our team of experts.
Comprehensive Coverage: We cover a wide range of math topics, from basic arithmetic to advanced calculus.
User-Friendly Interface: Our website is designed to be easy to navigate, so you can quickly find the information you need.
Community Support: Connect with other learners, share your knowledge, and get support from our community.

Don’t let math intimidate you. Visit WHAT.EDU.VN today and start your journey towards math success.

31. Test Your Knowledge: Quiz on Quotients

To test your understanding of quotients, try this short quiz:

What is the quotient of 36 divided by 4?
If you divide 50 by 7, what is the quotient and the remainder?
A class has 28 students. If they are divided into groups of 4, how many groups will there be?
What is the quotient of 144 divided by 12?
If you have 75 cookies and want to share them equally among 8 friends, how many cookies will each friend get, and how many will be left over?

Answers:

9
Quotient: 7, Remainder: 1
7
12
Each friend gets 9 cookies, and there will be 3 left over.

32. How to Use Online Resources to Practice Division

There are numerous online resources available to help you practice division and improve your skills.

32.1. Educational Websites

Websites like Khan Academy, IXL, and Math Playground offer interactive lessons, practice problems, and quizzes on division.

32.2. Mobile Apps

Mobile apps like Photomath, Mathway, and WolframAlpha can help you solve division problems, check your work, and learn step-by-step solutions.

32.3. Online Games

Online games like Prodigy, Cool Math Games, and Funbrain offer engaging ways to practice division skills.

33. The Benefits of Understanding Division Beyond the Classroom

A strong understanding of division extends far beyond the classroom. It is an essential skill for:

Cooking: Adjusting recipes and measuring ingredients accurately.
Home Improvement: Calculating measurements for projects and estimating costs.
Travel: Planning trips, calculating distances, and converting currencies.
Health and Fitness: Tracking calories, calculating body mass index (BMI), and monitoring exercise progress.
Everyday Problem Solving: Making informed decisions and solving practical problems in daily life.

34. Division and Its Role in Data Interpretation

In today’s data-driven world, understanding division is crucial for interpreting data and making informed decisions. Whether you’re analyzing sales figures, tracking website traffic, or interpreting survey results, division helps you:

Calculate Averages: Find the average value of a data set.
Determine Percentages: Calculate the percentage of a whole that a part represents.
Analyze Ratios: Compare different data points and identify trends.
Draw Conclusions: Make informed decisions based on data analysis.

35. Creative Ways to Teach Division

If you’re a teacher or parent looking for creative ways to teach division, here are some ideas:

Use Manipulatives: Use objects like counters, beads, or blocks to physically represent division problems.
Tell Stories: Create stories that involve division scenarios to make the concept more engaging.
Play Games: Use games like card games or board games to practice division skills in a fun way.
Real-World Projects: Assign real-world projects that require division, such as planning a party or designing a budget.
Visual Aids: Use visual aids like charts, diagrams, and videos to illustrate division concepts.

By using these creative methods, you can make learning division more enjoyable and effective for students of all ages.

36. The Future of Division: How Technology is Changing the Way We Divide

Technology is constantly changing the way we divide and perform mathematical calculations. From calculators to computers to mobile apps, technology has made division faster, easier, and more accessible than ever before.

36.1. AI and Machine Learning

Artificial intelligence (AI) and machine learning (ML) are being used to develop advanced algorithms that can perform complex division operations and solve mathematical problems with greater speed and accuracy.

36.2. Cloud Computing

Cloud computing enables us to access powerful computing resources and perform large-scale division operations from anywhere in the world.

36.3. Data Visualization

Data visualization tools make it easier to interpret and understand division results by presenting data in a clear and intuitive format.

As technology continues to evolve, we can expect even more innovative ways to divide and solve mathematical problems in the future.

37. Let WHAT.EDU.VN Be Your Guide to Mastering Division

We at WHAT.EDU.VN are dedicated to providing you with the resources and support you need to master division and other math concepts. Whether you’re a student, teacher, parent, or lifelong learner, we’re here to help you achieve your goals. Visit our website today to ask your questions, explore our resources, and connect with our community.

Address: 888 Question City Plaza, Seattle, WA 98101, United States

WhatsApp: +1 (206) 555-7890

Website: WHAT.EDU.VN

Don’t struggle with math alone. Let WHAT.EDU.VN be your trusted guide to success.

38. Ask Your Division Questions at WHAT.EDU.VN Today!

Are you ready to take your division skills to the next level? Do you have any questions or challenges you’d like to discuss? Visit WHAT.EDU.VN today and ask your questions for free! Our team of experts is standing by to provide you with the personalized guidance and support you need to succeed.

At what.edu.vn, we believe that everyone can master division with the right resources and support. So don’t wait—visit our website today and start your journey towards math excellence! We’re here to assist with any math related problems. Ask us anything today and get a free answer!