Are you struggling to understand what a radian is and how it’s used in math and physics? At WHAT.EDU.VN, we provide clear and concise explanations to help you grasp complex concepts effortlessly. A radian is the standard unit of angular measure, crucial for various calculations. This guide breaks down the definition, formulas, and conversions related to radians, making it easy for anyone to understand. Learn about angular measurements, unit circle and trigonometric functions.
1. What Is a Radian?
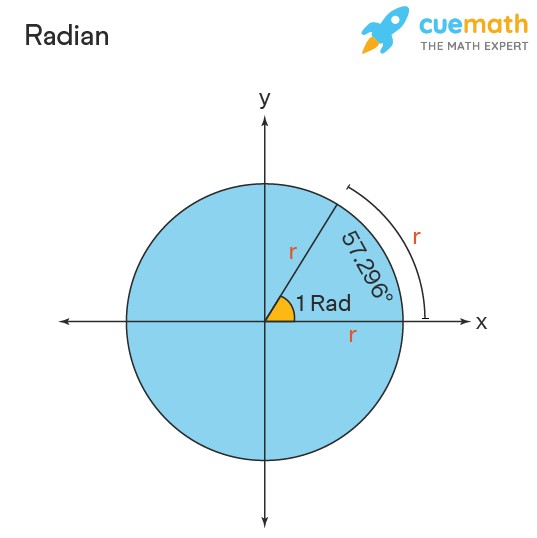
A radian is the Standard International (SI) unit used to measure angles. Specifically, one radian is the angle created at the center of a circle by an arc whose length equals the circle’s radius. Think of it like this: if you take the radius of a circle and lay it along the edge of the circle (the circumference), the angle formed from the center to that point is one radian. Approximately, one radian equals 57.296 degrees. In mathematical expressions, radians are represented as “rad” or with the symbol “c”. For example, 2.5 radians can be written as 2.5 rad or 2.5c.
1.1 Radian Definition Explained
Understanding the definition of a radian is essential for grasping its applications. Here are key points to remember:
- Symbol: Radians are denoted as “rad” or with the symbol “c” as a superscript.
- Units Omission: If an angle is written without any unit, it’s generally understood to be in radians.
- Examples: Examples of angles measured in radians include 3 rad, π/4, 2π/3, and 8c.
1.2 Common Uses of Radians
Radians are not just theoretical; they have practical applications in various fields:
- Calculus: Radians are the standard unit for measuring angles in calculus and most advanced mathematics branches.
- Physics: In physics, radians are preferred over degrees for angular measurements, especially in mechanics and wave motion.
2. Radian Formula
The radian formula provides a way to relate arc length, radius, and the angle subtended at the center of a circle. The fundamental idea is that one radian is formed when the arc length equals the radius.
2.1 The Core Formula
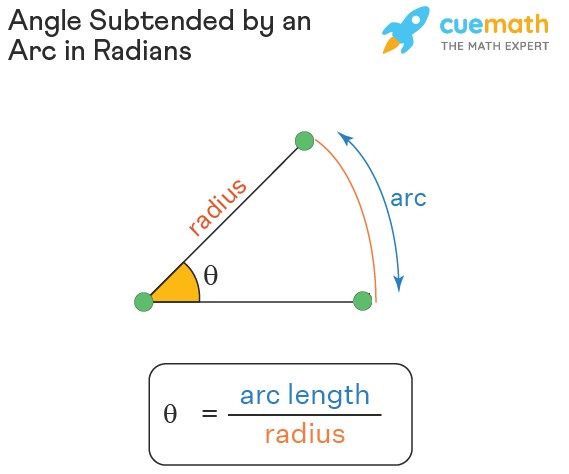
Mathematically, the angle in radians ((theta)) is defined as the ratio of the arc length ((s)) to the radius ((r)) of the circle:
[
theta = frac{s}{r}
]
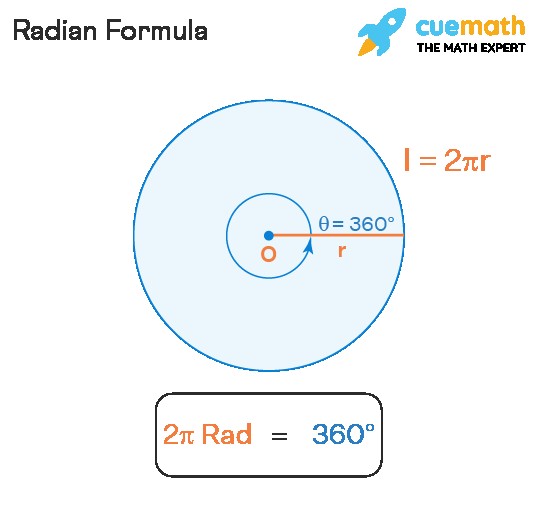
2.2 Deriving 2π = 360°
Consider the arc to be the entire circumference of the circle. The arc length then becomes (2pi r). The angle subtended at the center by the circumference is 360°. Therefore:
[
text{Angle subtended} = frac{text{arc length}}{text{radius}}
]
[
360^circ = frac{2pi r}{r}
]
[
360^circ = 2pi
]
Thus, the foundational radian formula is (2pi = 360^circ).
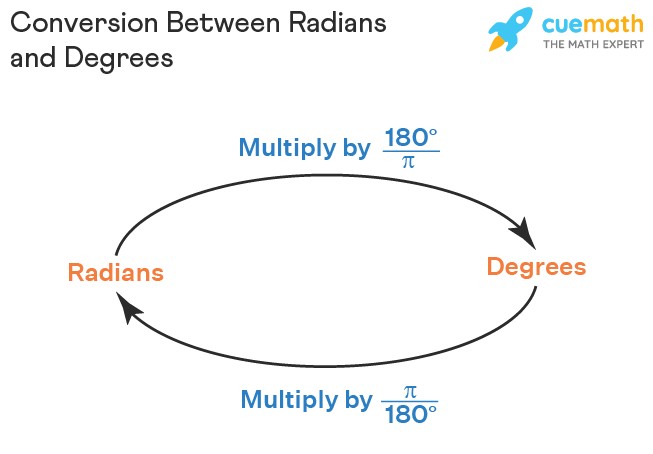
3. Conversion Between Radians and Degrees
Converting between radians and degrees is a common task in mathematics and physics. The basic relationship (2pi text{ radians} = 360^circ) forms the basis for these conversions.
3.1 Converting Radians to Degrees
To convert radians to degrees, use the formula:
[
1 text{ radian} = frac{180^circ}{pi}
]
So, to convert an angle from radians to degrees, multiply the angle in radians by (frac{180^circ}{pi}).
Examples:
- (frac{pi}{2} text{ radians} = frac{pi}{2} times frac{180^circ}{pi} = 90^circ)
- (frac{pi}{4} text{ radians} = frac{pi}{4} times frac{180^circ}{pi} = 45^circ)
- (frac{7pi}{6} text{ radians} = frac{7pi}{6} times frac{180^circ}{pi} = 210^circ)
- (2 text{ radians} = 2 times frac{180^circ}{pi} approx 114.59^circ)
A useful trick for angles in terms of (pi) is to replace (pi) with (180^circ):
- (frac{pi}{2} = frac{180^circ}{2} = 90^circ)
- (frac{pi}{4} = frac{180^circ}{4} = 45^circ)
- (frac{7pi}{6} = frac{7 times 180^circ}{6} = 210^circ)
3.2 Converting Degrees to Radians
To convert degrees to radians, use the formula:
[
1^circ = frac{pi}{180} text{ radians}
]
Multiply the angle in degrees by (frac{pi}{180}) to convert it to radians.
Examples:
- (90^circ = 90 times frac{pi}{180} = frac{pi}{2} text{ radians})
- (180^circ = 180 times frac{pi}{180} = pi text{ radians})
- (210^circ = 210 times frac{pi}{180} = frac{7pi}{6} text{ radians})
3.3 Radians and Degrees Table
Here’s a useful table with common angles in degrees and their equivalent values in radians:
| Degree | Radian |
|---|---|
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
4. Differences Between Radians and Degrees
Both radians and degrees are used to measure angles, but they differ in their definitions and applications.
| Feature | Radian | Degree |
|---|---|---|
| Definition | Angle subtended by an arc of length (r) in a circle of radius (r). | 1/360th part of a complete angle. |
| Notation | 1 rad or 1(^c) or simply 1. | 1°. |
| Conversion | Degrees to radians: multiply by (frac{pi}{180}). | Radians to degrees: multiply by (frac{180}{pi}). |
Key Points:
- To convert from degrees to radians, multiply by (frac{pi}{180}).
- To convert from radians to degrees, multiply by (frac{180}{pi}).
- When using the formula (text{Arc length} = text{radius} times text{angle}), ensure the angle is in radians.
5. Examples on Radians
Let’s solidify your understanding with some practical examples.
5.1 Example 1: Converting Degrees to Radians
Problem: Convert the following angles into radians: a) 120° b) 150°.
Solution:
To convert degrees to radians, multiply by (frac{pi}{180}).
a) (120^circ = 120 times frac{pi}{180} = frac{2pi}{3})
b) (150^circ = 150 times frac{pi}{180} = frac{5pi}{6})
Answer: a) (120^circ = frac{2pi}{3}) b) (150^circ = frac{5pi}{6})
5.2 Example 2: Finding Arc Length
Problem: What is the arc length of a circle with a radius of 6 inches if the angle subtended by the arc is 1.5 radians?
Solution:
Given:
- Radius (r = 6) inches
- Angle (theta = 1.5) radians
The formula for arc length (s) is (s = rtheta).
So, (s = 6 times 1.5 = 9) inches.
Answer: The arc length is 9 inches.
5.3 Example 3: Pendulum Arc Length
Problem: A pendulum with a length of 18 inches oscillates at an angle of 42 degrees. Find the length of the arc it covers, expressing the answer in terms of (pi).
Solution:
Given:
- Radius (r = 18) inches
- Angle (theta = 42^circ)
First, convert the angle to radians:
[
theta = 42^circ times frac{pi}{180} = frac{42pi}{180} text{ radians}
]
Now, use the arc length formula:
[
s = rtheta = 18 times frac{42pi}{180} = frac{756pi}{180} = 4.2pi text{ inches}
]
Answer: The length of the arc covered by the pendulum is (4.2pi) inches.
6. FAQs on Radian
6.1 What Exactly Is a Radian?
A radian is the SI unit for measuring angles, relating arc length to radius. One radian is the angle subtended at the center of a circle by an arc equal in length to the circle’s radius.
6.2 How Do I Convert Radians to Degrees?
To convert radians to degrees, multiply the angle in radians by (frac{180}{pi}). For example:
[
frac{3pi}{2} text{ radians} = frac{3pi}{2} times frac{180}{pi} = 270^circ
]
Thus, (frac{3pi}{2}) radians is equivalent to (270^circ).
6.3 What Is the Formula for Converting Degrees to Radians?
To convert degrees to radians, multiply the angle in degrees by (frac{pi}{180}). For example:
[
270^circ = 270 times frac{pi}{180} = frac{3pi}{2} text{ radians}
]
Thus, (270^circ) is equivalent to (frac{3pi}{2}) radians.
6.4 How Many Radians Are in a Complete Circle?
A complete circle is (360^circ). Since (360^circ = 2pi) radians, there are (2pi) radians in a complete circle.
6.5 What Is the Arc Length Formula Using Radians?
The arc length formula is given by:
[
text{Arc length} = text{radius} times text{angle in radians}
]
If the angle is in degrees, convert it to radians first.
6.6 What Is the Radian Formula in Terms of Arc Length?
To find the angle in radians subtended by an arc, divide the arc length by the radius of the circle:
[
theta text{ (in radians)} = frac{text{arc length}}{text{radius}}
]
6.7 What Is 1 Radian Equal To?
Since (2pi) radians ( = 360^circ), dividing by (2pi) gives:
[
1 text{ radian} = frac{360^circ}{2pi} = frac{180^circ}{pi} approx 57.296^circ
]
Thus, 1 radian is approximately equal to (57.296^circ). For example, (2 text{ radians} = 2 times 57.296^circ = 114.592^circ).
6.8 What Is the Measure of 0 Radians in Degrees?
To convert 0 radians to degrees, multiply by (frac{180}{pi}):
[
0 text{ radians} = 0 times frac{180}{pi} = 0^circ
]
Therefore, 0 radians is equal to (0^circ).
6.9 How Do You Convert 360 Degrees to Radians?
To convert (360^circ) to radians, multiply by (frac{pi}{180}):
[
360^circ = 360 times frac{pi}{180} = 2pi text{ radians}
]
Thus, (360^circ) is equivalent to (2pi) radians.
Understanding radians is crucial in various fields, and we hope this guide has made the concept clearer for you. Do you have more questions or need further clarification? Don’t hesitate to ask!
At WHAT.EDU.VN, we understand that finding quick and reliable answers can be challenging. That’s why we offer a platform where you can ask any question and receive prompt, accurate responses from knowledgeable individuals. Forget about the hassle of endless searching or worrying about consultation fees.
Ready to explore more and get your questions answered for free? Visit WHAT.EDU.VN today and experience the ease of learning with expert guidance. Our community is here to support your quest for knowledge, providing clear, understandable answers whenever you need them.
Contact Us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn