Are you curious about how to compare quantities and understand their relationships? At WHAT.EDU.VN, we provide clear explanations and solutions to your questions. A ratio is a comparison of two or more numbers, showing the relative sizes of different quantities. Let’s explore ratios, their calculations, equivalent forms, and practical applications. We’ll also cover essential aspects like the golden ratio and converting ratios to fractions, decimals, and percentages. By the end, you’ll have a solid understanding of ratios and how they’re used in various contexts, with access to our free consultation services for any further questions. Dive in to learn more about proportions, comparative quantities and scaling at WHAT.EDU.VN
1. What Is a Ratio?
A ratio compares two quantities of the same units, indicating how much of one quantity is present in another. Ratios come in two main types: part-to-part and part-to-whole. A part-to-part ratio shows the relationship between two distinct groups, such as the ratio of boys to girls in a class. A part-to-whole ratio shows the relationship between a specific group and the total, like the proportion of people who prefer reading books out of a larger group.
1.1. The Importance of Ratios
Ratios help simplify the interpretation of quantities by comparing the sizes of two or more quantities relative to each other. For instance, if a class has 30 girls and 20 boys, the ratio of girls to boys is 3:2. This clear comparison makes it easier to understand the composition of the class.
1.2. Part-to-Part Ratio Explained
The part-to-part ratio highlights the relationship between two separate groups. For example, in a classroom setting, the ratio of boys to girls could be 12:15. This tells us how the number of boys relates directly to the number of girls.
1.3. Part-to-Whole Ratio Explained
The part-to-whole ratio demonstrates the relationship between a specific group and the entire set. For instance, if 5 out of 10 people enjoy reading books, the part-to-whole ratio is 5:10, indicating that half of the group enjoys reading.
1.4. Real-World Applications of Ratios
Ratios are used in various real-world scenarios, including cooking, construction, and finance. They help in scaling recipes, planning construction projects, and analyzing financial data. Understanding ratios makes these tasks more manageable and accurate.
1.5. Simplifying Complex Comparisons
Ratios simplify complex comparisons by reducing the numbers to their simplest form, making it easier to understand and interpret the relationships between different quantities. This simplicity is crucial for effective decision-making in many fields.
2. Ratio Formula
The ratio formula helps compare the relationship between two numbers or quantities. The general representation of a ratio between two quantities, ‘a’ and ‘b,’ is a:b, read as ‘a is to b.’ This can also be expressed as a fraction a/b, which can be simplified similarly to simplifying fractions.
2.1. General Form of a Ratio
The general form of a ratio is expressed as a:b, where ‘a’ and ‘b’ are the two quantities being compared. This form provides a clear and concise way to represent the relationship between the two values.
2.2. Expressing Ratios as Fractions
Ratios can be expressed as fractions, such as a/b, which allows for easier simplification and comparison. This fractional representation is particularly useful in mathematical calculations and problem-solving.
2.3. Simplifying Ratio Fractions
To simplify a ratio fraction, find the greatest common factor (GCF) of the numerator and denominator, then divide both by the GCF. This simplifies the ratio to its lowest terms, making it easier to understand and work with.
2.4. Example: Boys to Girls Ratio
Consider a class of 50 students, with 23 girls and the rest boys. The number of boys is 50 – 23 = 27. The ratio of boys to girls is 27:23, showing the proportion of each gender in the class.
2.5. Practical Calculation Example
If you need 15 cups of flour and 20 cups of sugar for pancakes, the ratio of flour to sugar is 15:20. Simplifying this gives 3:4, meaning for every 3 cups of flour, you need 4 cups of sugar.
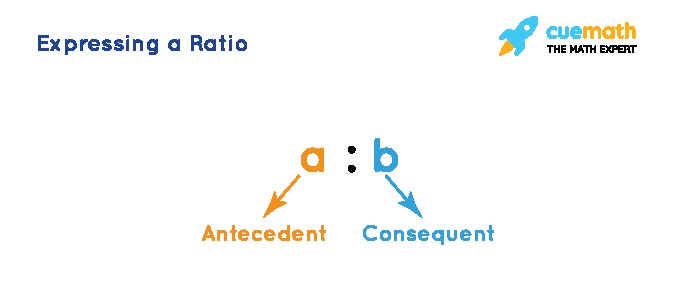
2.6. Understanding Antecedent and Consequent
In a ratio a:b, ‘a’ is the antecedent (the first term) and ‘b’ is the consequent (the second term). Understanding these terms helps in correctly interpreting and using the ratio.
3. Calculation of Ratios
To calculate the ratio of two quantities, follow a step-by-step approach. Start by identifying the quantities, express them as a fraction, simplify the fraction if possible, and then represent the result as a ratio.
3.1. Step 1: Identify the Quantities
The first step in calculating a ratio is to identify the two quantities that you want to compare. This involves understanding what each quantity represents and ensuring they are in the same units.
3.2. Step 2: Write as a Fraction
Once you have identified the quantities, write them as a fraction a/b. This step is crucial for simplifying the ratio and making it easier to work with.
3.3. Step 3: Simplify the Fraction
Simplify the fraction by finding the greatest common factor (GCF) of the numerator and denominator and dividing both by it. This step reduces the ratio to its simplest form.
3.4. Step 4: Express as a Ratio
Finally, express the simplified fraction as a ratio a:b. This is the standard way to represent the relationship between the two quantities.
3.5. Example: Flour to Sugar Ratio
If a recipe requires 15 cups of flour and 20 cups of sugar, the ratio of flour to sugar is calculated as follows:
- Quantities: 15 cups of flour and 20 cups of sugar
- Fraction: 15/20
- Simplified Fraction: 3/4
- Ratio: 3:4
This means for every 3 cups of flour, you need 4 cups of sugar.
3.6. Ensuring Same Units
Before calculating a ratio, ensure that both quantities are in the same units. If not, convert them to the same unit to ensure accurate comparison.
4. How to Simplify Ratios?
Simplifying ratios involves reducing the two terms to their lowest form, making the ratio easier to understand. The process is similar to simplifying fractions.
4.1. Step 1: Write as a Fraction
Write the given ratio a:b as a fraction a/b. This step is essential for applying simplification techniques.
4.2. Step 2: Find the Greatest Common Factor (GCF)
Determine the greatest common factor (GCF) of ‘a’ and ‘b.’ The GCF is the largest number that divides both ‘a’ and ‘b’ without leaving a remainder.
4.3. Step 3: Divide by the GCF
Divide both the numerator and the denominator of the fraction by the GCF to obtain the simplified fraction. This step reduces the ratio to its simplest form.
4.4. Step 4: Represent as a Simplified Ratio
Represent the simplified fraction as a ratio to get the final result. This is the simplest form of the original ratio.
4.5. Example: Simplifying 18:10
To simplify the ratio 18:10, follow these steps:
- Fraction: 18/10
- GCF of 18 and 10: 2
- Divide by GCF: (18÷2)/(10÷2) = 9/5
- Simplified Ratio: 9:5
Thus, the simplified ratio of 18:10 is 9:5.
4.6. Understanding Lowest Terms
Expressing ratios in their lowest terms makes them easier to understand and compare. Simplified ratios provide a clearer representation of the relationship between the two quantities.
5. Equivalent Ratios
Equivalent ratios are ratios that represent the same value, similar to equivalent fractions. You can create equivalent ratios by multiplying or dividing both the antecedent and consequent of a given ratio by the same non-zero number.
5.1. Creating Equivalent Ratios
To create equivalent ratios, multiply or divide both terms of the original ratio by the same number. This maintains the proportion between the two quantities.
5.2. Multiplying Antecedent and Consequent
When the antecedent and consequent of the ratio 1:3 are multiplied by 3, we get (1 × 3) : (3 × 3), which simplifies to 3:9. Here, 1:3 and 3:9 are equivalent ratios.
5.3. Dividing Antecedent and Consequent
When both terms of the ratio 20:10 are divided by 10, we get 2:1. In this case, 20:10 and 2:1 are equivalent ratios.
5.4. Infinite Number of Equivalent Ratios
An infinite number of equivalent ratios can be found for any given ratio by multiplying the antecedent and consequent by a positive integer. This allows for scaling the ratio up or down while maintaining the same proportion.
5.5. Example: Finding Equivalent Ratios of 1:4
To find four equivalent ratios of 1:4, multiply both terms of the ratio by 2, 3, 6, and 9:
- Multiply by 2: 2:8
- Multiply by 3: 3:12
- Multiply by 6: 6:24
- Multiply by 9: 9:36
5.6. Using Equivalent Ratios in Problem Solving
Equivalent ratios are useful in solving proportion problems, where you need to find an unknown quantity based on a known ratio. By using equivalent ratios, you can easily scale the quantities to find the missing value.
6. Ratio Table
A ratio table is a structured list that contains equivalent ratios of a given ratio. These tables help visualize the relationship between the original ratio and its equivalent forms.
6.1. Structure of a Ratio Table
A ratio table typically consists of columns representing the quantities in the ratio and rows listing the equivalent ratios. The equivalent ratios are related to each other through multiplication or division by a common factor.
6.2. Creating a Ratio Table
To create a ratio table, start with a given ratio and generate equivalent ratios by multiplying or dividing both terms by the same number. List these equivalent ratios in a structured table.
6.3. Multiplication in Ratio Tables
Equivalent ratios in a table are often generated by multiplying both terms of the original ratio by a common factor. This maintains the proportion between the quantities.
6.4. Division in Ratio Tables
Division can also be used to generate equivalent ratios, especially when simplifying larger ratios to their smaller, equivalent forms.
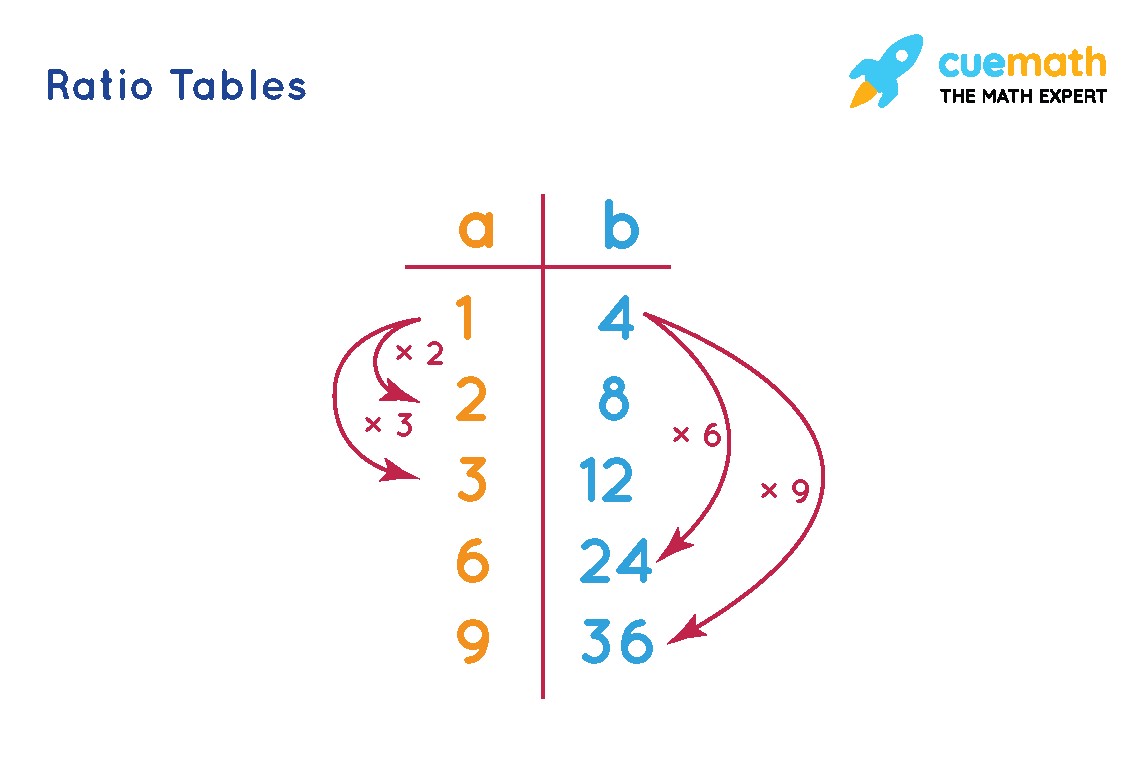
6.5. Example: Ratio Table for 1:4
Here’s a ratio table showing the relationship between the ratio 1:4 and four of its equivalent ratios:
| Original Ratio | Equivalent Ratio 1 | Equivalent Ratio 2 | Equivalent Ratio 3 | Equivalent Ratio 4 |
|---|---|---|---|---|
| 1:4 | 2:8 | 3:12 | 6:24 | 9:36 |
In this table, each equivalent ratio is obtained by multiplying both terms of the original ratio (1:4) by a common factor (2, 3, 6, and 9).
6.6. Applications of Ratio Tables
Ratio tables are useful in various applications, such as scaling recipes, converting measurements, and solving proportion problems. They provide a visual aid to understand and work with equivalent ratios.
7. Ratio Examples
Practical examples help illustrate how ratios are used in real-world scenarios. These examples cover various situations, from determining the ratio of boys to girls in an auditorium to simplifying complex ratios.
7.1. Example 1: Boys to Girls in an Auditorium
Problem: There are 49 boys and 28 girls in a school auditorium. Express the ratio of the number of boys to that of girls.
Solution:
- Number of boys: 49
- Number of girls: 28
- GCF of 49 and 28: 7
- Simplified Ratio: (49 ÷ 7)/(28 ÷ 7) = 7/4
Therefore, the ratio of the number of boys to that of girls is 7:4.
7.2. Example 2: Students in a Music Class
Problem: A music class has 30 students. 10 of them are adults, and the rest are children. What is the ratio of the number of children to the total number of students in the music class?
Solution:
- Total number of students: 30
- Number of adults: 10
- Number of children: 30 – 10 = 20
- Ratio of children to total students: 20:30
- Simplified Ratio: 2:3
Thus, the ratio of the number of children to the total number of students in the music class is 2:3.
7.3. Example 3: Simplifying a Given Ratio
Problem: Simplify the given ratio, 87:75.
Solution:
- Ratio: 87:75
- GCF of 87 and 75: 3
- Simplified Ratio: (87 ÷ 3)/(75 ÷ 3) = 29/25
Therefore, the ratio 87:75 in the simplest form is 29:25.
7.4. Importance of Simplifying Ratios
Simplifying ratios makes them easier to understand and compare. Simplified ratios provide a clearer representation of the relationship between the two quantities, facilitating better decision-making and problem-solving.
7.5. Practical Application of Ratios
Ratios are used in various practical applications, such as scaling recipes, calculating proportions in construction projects, and analyzing financial data. Understanding and applying ratios can improve accuracy and efficiency in these tasks.
8. Practice Questions on Ratio
Practicing with ratio-related questions helps reinforce understanding and application. These questions cover various aspects of ratios, from simple calculations to more complex problem-solving.
8.1. Question 1: Ratio of Apples to Oranges
Problem: In a fruit basket, there are 12 apples and 18 oranges. What is the ratio of apples to oranges in the simplest form?
Solution:
- Number of apples: 12
- Number of oranges: 18
- Ratio of apples to oranges: 12:18
- GCF of 12 and 18: 6
- Simplified Ratio: (12 ÷ 6)/(18 ÷ 6) = 2/3
Therefore, the simplified ratio of apples to oranges is 2:3.
8.2. Question 2: Dividing Money in a Ratio
Problem: Divide $500 between two friends, Alex and Ben, in the ratio 3:2. How much does each friend receive?
Solution:
- Ratio: 3:2
- Total parts: 3 + 2 = 5
- Value of one part: $500 ÷ 5 = $100
- Amount Alex receives: 3 × $100 = $300
- Amount Ben receives: 2 × $100 = $200
Therefore, Alex receives $300, and Ben receives $200.
8.3. Question 3: Scaling a Recipe
Problem: A recipe for cookies requires 2 cups of flour and 1 cup of sugar. If you want to make a larger batch using 6 cups of flour, how much sugar do you need?
Solution:
- Original ratio of flour to sugar: 2:1
- New amount of flour: 6 cups
- Scale factor: 6 ÷ 2 = 3
- Amount of sugar needed: 1 × 3 = 3 cups
Therefore, you need 3 cups of sugar.
8.4. Question 4: Ratio of Cats to Dogs
Problem: In a neighborhood, there are 25 cats and 15 dogs. What is the ratio of cats to dogs in the simplest form?
Solution:
- Number of cats: 25
- Number of dogs: 15
- Ratio of cats to dogs: 25:15
- GCF of 25 and 15: 5
- Simplified Ratio: (25 ÷ 5)/(15 ÷ 5) = 5/3
Therefore, the simplified ratio of cats to dogs is 5:3.
8.5. Benefits of Practice Questions
Solving practice questions enhances understanding and builds confidence in applying ratio concepts. Regular practice improves problem-solving skills and reinforces the ability to work with ratios effectively.
9. FAQs on Ratio
This section addresses frequently asked questions about ratios, providing clear and concise answers to common queries.
9.1. What is Ratio in Math?
A ratio is a comparison between two numbers of the same unit to check how much bigger one number is than the other. For example, if marks scored in a test are 7 out of 10, the ratio of marks obtained to the total marks is 7:10.
9.2. What are the Ways of Writing a Ratio?
A ratio can be written by separating the two quantities using a colon (:) or in fractional form. For example, if there are 4 apples and 8 melons, the ratio of apples to melons can be written as 4:8 or 4/8, which simplifies to 1:2.
9.3. How to Calculate the Ratio Between Two Numbers?
To calculate the ratio of two quantities, follow these steps:
- Note the quantities of both items.
- Write it in fractional form a/b.
- Simplify the fraction if possible.
- Express the simplified fraction as a ratio.
For example, if 14 cups of butter and 28 cups of sugar are needed, the ratio of butter to sugar is 14/28, which simplifies to 1:2.
9.4. How to Find Equivalent Ratios?
Equivalent ratios represent the same value when simplified. Multiply or divide both terms of the ratio by the same number. For example, multiplying the ratio 1:4 by 2 gives (1 × 2)/(4 × 2) = 2/8 or 2:8.
9.5. What is a Ratio Table?
A ratio table is a list of equivalent ratios obtained by multiplying or dividing both quantities by the same value. For example, starting with 1:3, successive rows would have 2:6, 3:9, 4:12, and so on.
9.6. What is the Golden Ratio?
The golden ratio is a special number approximately equal to 1.618, symbolized by the Greek letter phi (ϕ). It is used in art, geometry, and architecture because it is believed to create the most pleasing shapes.
9.7. Why are Ratios Important?
Ratios are important because they allow us to express quantities in a way that is easier to interpret. They help compare the size of two or more quantities with respect to each other. For example, a class with 30 girls and 20 boys has a girl-to-boy ratio of 3:2.
9.8. What is the Ratio Formula?
The ratio formula compares the relationship between two numbers or quantities. The general form of representing a ratio between two quantities ‘a’ and ‘b’ is a:b, read as ‘a is to b.’
9.9. What is Ratio and Proportion?
A ratio is the comparison between two quantities of the same unit, written as a/b or a:b. A proportion is an equality of two ratios, such as a:b = c:d, used to write equivalent ratios and solve for unknown quantities.
9.10. How to Compare Ratios?
To compare ratios, write them as fractions, reduce the fractions, find the least common multiple (LCM) of the denominators, make the denominators equal, and then compare the numerators. For example, comparing 1:2 and 2:3 involves making the fractions 1/2 and 2/3 have a common denominator of 6, resulting in 3/6 and 4/6, showing that 2:3 > 1:2.
9.11. How to Convert Ratios to Fractions?
Write the ratio in the form of a fraction with the antecedent as the numerator and the consequent as the denominator. For example, the ratio 3:5 can be written as 3/5.
9.12. How to Convert Fractions to Ratios?
Reduce the fraction to its lowest terms and then write the numerator as the antecedent and the denominator as the consequent. For example, the fraction 16/48 is reduced to 1/3 and expressed as the ratio 1:3.
9.13. How to Convert Ratios to Decimals?
Write the ratio as a fraction and divide the numerator by the denominator. For example, 3:7 can be written as 3/7, which equals approximately 0.428.
9.14. How to Convert Ratios to Percentages?
Write the ratio as a fraction, multiply the fraction by 100, and add the percentage symbol. For example, 5:6 can be written as 5/6, which is approximately 83.33%.
Are you struggling to find quick, free answers to your questions? Do you need help understanding complex topics? At WHAT.EDU.VN, we provide a platform where you can ask any question and receive timely, accurate responses from knowledgeable individuals.
We understand the challenges of finding reliable information and the frustration of not knowing where to turn for help. That’s why we’ve created a community-driven platform that offers free consultations and expert advice on a wide range of subjects.
Whether you’re a student tackling homework, a professional seeking career guidance, or simply a curious individual eager to learn, WHAT.EDU.VN is here to support you.
Ready to get your questions answered? Visit WHAT.EDU.VN today and experience the convenience of free, expert consultations. Our services are available to users worldwide, ensuring that knowledge is accessible to everyone.
Contact us:
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: what.edu.vn