Are you curious about What Is A Rational Number? Look no further than WHAT.EDU.VN for a clear and comprehensive explanation. A rational number is any number that can be expressed as a fraction p/q, where p and q are integers and q is not zero. We’ll break down the definition, explore different types, and provide plenty of examples to solidify your understanding of rational numbers and related mathematical concepts.
Want to explore more about rational numbers and get free answers? Visit WHAT.EDU.VN today to ask your questions!
1. Defining Rational Numbers: A Comprehensive Overview
A rational number is fundamentally any number that can be written as a ratio of two integers, p and q, where q isn’t zero. This means that every fraction you encounter, with the condition that the denominator is not zero, is a rational number. The result of dividing these numbers will be a decimal that either terminates (ends) or repeats in a pattern. Understanding this definition is crucial for grasping more complex mathematical concepts.
1.1. Identifying Rational Numbers: Key Conditions
To determine if a number qualifies as rational, verify these conditions:
- Fraction Form: Can the number be written in the form of p/q, where p and q are integers, and q is not equal to zero?
- Decimal Representation: Can the ratio p/q be simplified into a decimal that either terminates or repeats?
If both conditions are met, you’re dealing with a rational number.
1.2. The Set of Rational Numbers: An Overview
The set of rational numbers encompasses a broad range of numbers:
- Includes Various Numbers: It features positive numbers, negative numbers, and zero.
- Expressible as a Fraction: Each rational number can be shown as a fraction.
1.3. Rational Number Examples:
| p | q | p/q | Rational |
|---|---|---|---|
| 10 | 2 | 10/2 = 5 | Yes |
| 1 | 1000 | 1/1000 = 0.001 | Yes |
| 50 | 10 | 50/10 = 5 | Yes |
| -3 | 4 | -3/4 = -0.75 | Yes |
| 0 | 5 | 0/5 = 0 | Yes |
| 22 | 7 | 22/7 ≈ 3.142857 | Yes |

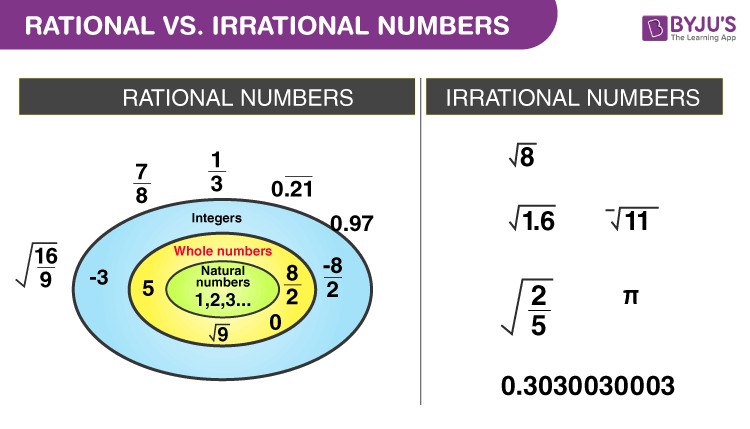

2. Exploring Types of Rational Numbers
To be classified as rational, a number must be expressible as a fraction with integers in the numerator and denominator, the denominator being non-zero.
2.1. Visualizing Number Sets
Understanding the relationship between different sets of numbers can be simplified using a visual representation:
- Real Numbers (R): Encompass all rational numbers (Q).
- Integers (Z): A subset of real numbers.
- Natural Numbers (N): Contained within integers.
Additionally, all whole numbers are rational because they can be expressed as a fraction with a denominator of 1.
2.2. Standard Form of Rational Numbers
A rational number is in standard form if the greatest common factor between the numerator and denominator is 1, and the denominator is positive. For example, 12/36 simplifies to 1/3, which is in standard form.
2.3. Positive and Negative Rational Numbers
Rational numbers can be positive or negative. If p/q is positive, both p and q are positive or both are negative. If p/q is negative, either p or q is negative.
- -(p/q) = (-p)/q = p/(-q)
Positive vs. Negative Rational Numbers:
| Positive Rational Numbers | Negative Rational Numbers |
|---|---|
| Numerator and denominator have the same sign. | Numerator and denominator have opposite signs. |
| Greater than 0. | Less than 0. |
| Examples: 12/17, 9/11, 3/5, -2/-3, -5/-7 | Examples: -2/17, 9/-11, -1/5, 2/-3, 5/-7 |
3. Arithmetic Operations on Rational Numbers
Arithmetic operations form the bedrock of working with rational numbers. Here’s a look at how addition, subtraction, multiplication, and division are handled with rational numbers, denoted as p/q and s/t.
3.1. Addition
To add two rational numbers, p/q and s/t, you need a common denominator. The formula is (pt + qs) / qt.
Example: 1/2 + 3/4 = (14 + 32) / (2*4) = (4 + 6) / 8 = 10/8 = 5/4
3.2. Subtraction
For subtraction, a common denominator is also required. Subtracting s/t from p/q results in (pt – qs) / qt.
Example: 1/2 – 3/4 = (14 – 32) / (2*4) = (4 – 6) / 8 = -2/8 = -1/4
3.3. Multiplication
Multiplication of rational numbers involves multiplying the numerators and the denominators separately: (p/q) × (s/t) = (p×s) / (q×t).
Example: 1/2 × 3/4 = (1×3) / (2×4) = 3/8
3.4. Division
Dividing p/q by s/t is the same as multiplying p/q by the reciprocal of s/t: (p/q) ÷ (s/t) = (p/q) × (t/s) = (p×t) / (q×s).
Example: 1/2 ÷ 3/4 = (1×4) / (2×3) = 4/6 = 2/3
4. Multiplicative Inverse of Rational Numbers
The multiplicative inverse, also known as the reciprocal, of a rational number p/q is q/p, such that (p/q) × (q/p) = 1.
Example: The multiplicative inverse of 4/7 is 7/4, because (4/7) × (7/4) = 1.
5. Properties of Rational Numbers
Rational numbers possess several key properties due to their classification as a subset of real numbers.
- Closure: Addition, subtraction, and multiplication of rational numbers always result in another rational number.
- Equivalence: Multiplying or dividing both the numerator and denominator by the same non-zero number does not change the value of the rational number.
- Additive Identity: Adding zero to any rational number leaves the number unchanged.
For a more in-depth understanding, explore additional properties of rational numbers on WHAT.EDU.VN.
6. Rational Numbers vs. Irrational Numbers
The key difference lies in their representation. Rational numbers can be expressed as a simple fraction with non-zero denominators, while irrational numbers cannot.
- Rational Numbers: Can be positive, negative, or zero. In standard notation, a negative rational number is represented with the negative sign either in front of the fraction or with the numerator (e.g., -5/2).
- Irrational Numbers: Cannot be written as a simple fraction. They have endless non-repeating digits after the decimal point. Common examples include Pi (π ≈ 3.14159…) and the square root of 2 (√2 ≈ 1.414213…).
7. Finding Rational Numbers Between Two Given Numbers
Infinite rational numbers exist between any two rational numbers. Here are two common methods to find them:
7.1. Method 1: Equivalent Fractions
Find equivalent fractions for the given rational numbers with a common denominator, and then identify the rational numbers that fall between them.
7.2. Method 2: Mean Value
Calculate the mean (average) of the two rational numbers. The mean will be a rational number between the two original numbers. To find more rational numbers, repeat the process using the mean and one of the original numbers.
8. Video Resources on Rational Numbers
For a visual learning experience, check out video lessons on rational numbers available on various educational platforms.
9. Solved Examples: Understanding Rational Numbers
Let’s apply our understanding with some examples.
Example 1: Identify each number as rational or irrational: ¾, 90/12007, 12, and √5.
Solution:
- ¾: Rational, as it can be expressed as a fraction (3/4 = 0.75).
- 90/12007: Rational, as it is a fraction.
- 12: Rational, as it can be written as 12/1.
- √5: Irrational, as its value (approximately 2.2360679775…) is non-terminating and non-repeating, and therefore cannot be written as a fraction.
Example 2: Determine whether the mixed fraction 1 1/2 is a rational number.
Solution:
- First, convert the mixed fraction to an improper fraction: 1 1/2 = 3/2
- Numerator = 3, which is an integer.
- Denominator = 2, which is an integer and not equal to zero.
- Therefore, 3/2 is a rational number.
Example 3: Determine whether the given numbers are rational or irrational: (a) 1.75 (b) 0.01 (c) 0.5 (d) 0.09 (e) √3
Solution:
Convert each decimal number into a fraction form (p/q). If the denominator is not equal to zero, then the number is rational; otherwise, it is irrational.
| Decimal Number | Fraction | Rational Number |
|---|---|---|
| 1.75 | 7/4 | Yes |
| 0.01 | 1/100 | Yes |
| 0.5 | 1/2 | Yes |
| 0.09 | 9/100 | Yes |
| √3 | ? | No |
10. Frequently Asked Questions (FAQs) on Rational Numbers
Here are some common questions to further clarify the concept of rational numbers.
Q1. What are rational numbers? Give Examples.
Rational numbers are numbers that can be expressed in the form p/q, where p and q are integers, and q is not equal to 0. Examples include 1/3, 2/4, 1/5, and 9/3.
Q2. What is the difference between rational and irrational numbers?
A rational number can be expressed as the ratio of two integers, with a non-zero denominator. An irrational number cannot be expressed in this form. Rational numbers have terminating or repeating decimals, while irrational numbers have non-terminating, non-recurring decimals. An example of a rational number is 10/2, and an example of an irrational number is Pi (π ≈ 3.141592653589…).
Q3. Is 0 a rational number?
Yes, 0 is a rational number because it is an integer and can be written as 0/1, where the denominator is a non-zero integer. It fits the form p/q = 0/1.
Q4. Is 7 a rational number?
Yes, 7 is a rational number because it can be written as the ratio 7/1.
Q5. Is 3.14 a rational number?
Yes, 3.14 is a rational number because it terminates and can be expressed as the fraction 314/100. However, π (pi) is not a rational number because its exact value (3.141592653589793238…) is non-terminating and non-recurring.
Q6. Find a rational number between 3 and 4.
A rational number between 3 and 4 is (3+4)/2 = 7/2 = 3.5
Q7. What is the denominator of the rational number?
The denominator of a rational number can be any real number except 0.
Q8. Is Pi(π) a rational number?
No, Pi (π) is not a rational number; it is an irrational number with a value approximately equal to 3.14159….
Do you still have questions about rational numbers? Don’t struggle alone! At WHAT.EDU.VN, we provide a platform for you to ask any question and receive free answers from experts and community members. Stop searching endlessly and get the specific information you need, tailored to your understanding.
Ready to simplify your understanding of math?
Visit WHAT.EDU.VN today! Our services are designed to help you:
- Ask any question, anytime: No matter how complex or simple, we’re here to provide answers.
- Receive fast, accurate responses: Our community of experts is dedicated to giving you the information you need quickly.
- Access a wealth of knowledge for free: Learning shouldn’t break the bank. Our platform is completely free to use.
Address: 888 Question City Plaza, Seattle, WA 98101, United States
WhatsApp: +1 (206) 555-7890
Website: WHAT.EDU.VN
Take advantage of our free question-and-answer service at what.edu.vn and make learning easier and more accessible than ever before. We’re here to help you succeed.
