What Is A Supplementary Angle? Unlock the secrets of supplementary angles with WHAT.EDU.VN. Our guide offers clear explanations, practical examples, and helpful tips, ensuring you grasp this essential geometry concept. Discover more about angle pairs and straight lines today.
1. Understanding Supplementary Angles: The Basics
Supplementary angles are two angles whose measures add up to 180 degrees. This fundamental concept in geometry helps us understand the relationships between angles and lines. When these two angles are adjacent, they form a straight line.
Think of it like this: Imagine a pizza cut into two slices. If the angles of those two slices add up to form a half-circle (180 degrees), then those angles are supplementary. This applies whether the angles are next to each other or separated.
2. Defining Supplementary Angles
Formally, two angles, ∠A and ∠B, are supplementary if:
∠A + ∠B = 180°
This definition means that if you know one angle, you can always find its supplement by subtracting its measure from 180 degrees.
For example, if ∠A = 60°, then ∠B = 180° – 60° = 120°. Therefore, 60° and 120° are supplementary angles.
3. Key Properties of Supplementary Angles
Understanding the properties of supplementary angles can help you solve geometry problems more efficiently:
- Sum to 180°: This is the defining property. The measures of the two angles always add up to 180 degrees.
- Form a Straight Line: When adjacent, supplementary angles create a straight line, also known as a straight angle.
- Not Necessarily Adjacent: Supplementary angles do not have to be next to each other. They simply need to add up to 180 degrees.
- One Acute, One Obtuse, or Two Right Angles: Supplementary angles can consist of one acute angle (less than 90°) and one obtuse angle (greater than 90° but less than 180°), or they can both be right angles (exactly 90°).
4. Examples of Supplementary Angles in Action
Let’s look at some examples to solidify your understanding:
- 135° and 45°: 135° + 45° = 180°. These angles are supplementary.
- 90° and 90°: 90° + 90° = 180°. Two right angles are supplementary.
- 60° and 120°: 60° + 120° = 180°. These angles are also supplementary.
- 20° and 160°: 20° + 160° = 180°. Another example of supplementary angles.
- 75° and 105°: 75° + 105° = 180°. This pair fits the definition as well.
5. Adjacent vs. Non-Adjacent Supplementary Angles
Supplementary angles can be classified as either adjacent or non-adjacent, depending on their position relative to each other.
5.1. Adjacent Supplementary Angles
Adjacent supplementary angles share a common vertex and a common side. They lie next to each other, forming a straight line.
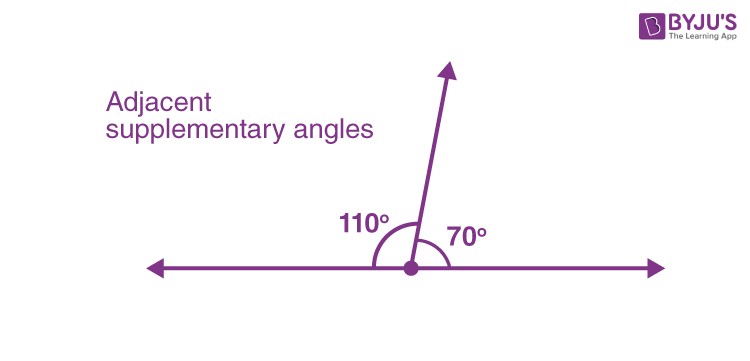Adjacent Supplementary Angles
In the image above, the two angles are adjacent because they share a common vertex and side. Together, they form a straight line. An example of this would be angles measuring 70° and 110°.
5.2. Non-Adjacent Supplementary Angles
Non-adjacent supplementary angles do not share a common vertex or a common side. They are separate angles that, when added together, equal 180 degrees.
For example, consider two separate angles, one measuring 50° and the other measuring 130°. They are non-adjacent because they are not connected, but they are supplementary because 50° + 130° = 180°.
6. How to Calculate Supplementary Angles
Calculating supplementary angles is straightforward. If you know one angle, you can find its supplement using the formula:
Supplementary Angle = 180° – Given Angle
Let’s illustrate this with a few examples:
-
Example 1: Find the supplement of an angle measuring 30°.
- Supplementary Angle = 180° – 30° = 150°
-
Example 2: Find the supplement of an angle measuring 95°.
- Supplementary Angle = 180° – 95° = 85°
-
Example 3: Find the supplement of an angle measuring 120°.
- Supplementary Angle = 180° – 120° = 60°
7. Supplementary Angle Theorem Explained
The Supplementary Angle Theorem states that if two angles are supplementary to the same angle, then those two angles are congruent (equal in measure).
7.1. Proof of the Theorem
Let’s say we have three angles: ∠X, ∠Y, and ∠Z. If ∠X and ∠Y are both supplementary to ∠Z, then:
∠X + ∠Z = 180°
∠Y + ∠Z = 180°
From these two equations, we can deduce that:
∠X + ∠Z = ∠Y + ∠Z
Subtracting ∠Z from both sides, we get:
∠X = ∠Y
Therefore, ∠X and ∠Y are congruent.
7.2. Practical Application
This theorem is useful in geometry proofs and problem-solving. It allows you to conclude that two angles are equal if they are both supplements of the same angle, simplifying complex geometric relationships.
8. Supplementary Angles vs. Complementary Angles
It’s easy to confuse supplementary and complementary angles, but they have distinct definitions.
| Feature | Complementary Angles | Supplementary Angles |
|---|---|---|
| Definition | Sum to 90° | Sum to 180° |
| Equation | ∠A + ∠B = 90° | ∠A + ∠B = 180° |
| Angle Types | Acute angles | Can include obtuse |
| Common Application | Right triangles | Straight lines |
| Mnemonic | “Corner” (90°) | “Straight” (180°) |
| Example Angles | 30° and 60° | 60° and 120° |
| Geometric Formation | Right angle | Straight angle |
| Typical Use Cases | Triangle properties | Linear pairs |
| Degree Relationship | Half of a straight | Full straight angle |
| Practical Scenario | Roof pitch | Compass direction |
- Complementary Angles: Two angles are complementary if their measures add up to 90 degrees. These angles form a right angle.
- Supplementary Angles: As we’ve discussed, two angles are supplementary if their measures add up to 180 degrees. These angles form a straight line.
9. Real-World Applications of Supplementary Angles
Supplementary angles are not just abstract geometric concepts; they have practical applications in various fields.
- Architecture: Architects use supplementary angles to design structures and ensure stability. For example, roof angles and support beams often involve supplementary relationships.
- Engineering: Engineers apply the principles of supplementary angles in designing bridges, machines, and other structures. Accurate angle calculations are crucial for structural integrity.
- Navigation: Navigators use angles to determine direction and position. Supplementary angles can help calculate bearings and courses.
- Construction: Builders rely on angle measurements to construct walls, floors, and roofs. Supplementary angles ensure that structures are square and aligned correctly.
- Art and Design: Artists and designers use angles to create visually appealing compositions. Supplementary angles can contribute to balance and harmony in artwork.
10. Common Mistakes to Avoid When Working with Supplementary Angles
To ensure accuracy when working with supplementary angles, avoid these common mistakes:
- Confusing with Complementary Angles: Remember that supplementary angles add up to 180°, while complementary angles add up to 90°.
- Assuming Adjacency: Supplementary angles do not need to be adjacent. They simply need to add up to 180°.
- Incorrectly Subtracting from 180°: Double-check your subtraction when finding the supplement of an angle.
- Forgetting Units: Always include the degree symbol (°) when expressing angle measurements.
- Misinterpreting Diagrams: Be careful when interpreting diagrams. Ensure you understand which angles are being referred to.
11. Practice Problems: Test Your Knowledge
Let’s put your knowledge to the test with some practice problems:
Problem 1: Angle A measures 115°. What is the measure of its supplement, angle B?
Solution:
∠B = 180° – ∠A
∠B = 180° – 115°
∠B = 65°
Therefore, the supplement of angle A is 65°.
Problem 2: Two angles are supplementary. One angle measures 48°. What is the measure of the other angle?
Solution:
Let the unknown angle be x.
x + 48° = 180°
x = 180° – 48°
x = 132°
Therefore, the other angle measures 132°.
Problem 3: Angle P and angle Q are supplementary. If angle P measures 72°, what is the measure of angle Q?
Solution:
∠Q = 180° – ∠P
∠Q = 180° – 72°
∠Q = 108°
Therefore, angle Q measures 108°.
Problem 4: Determine if the angles 55° and 135° are supplementary.
Solution:
55° + 135° = 190°
Since the sum is not 180°, these angles are not supplementary.
Problem 5: Angle X and angle Y are supplementary. If angle X is three times the size of angle Y, find the measures of both angles.
Solution:
Let ∠Y = y
Then ∠X = 3y
Since they are supplementary:
3y + y = 180°
4y = 180°
y = 45°
So, ∠Y = 45° and ∠X = 3 * 45° = 135°
12. Advanced Concepts Involving Supplementary Angles
Once you have a solid understanding of the basics, you can explore more advanced concepts involving supplementary angles.
12.1. Linear Pairs
A linear pair is a pair of adjacent angles formed when two lines intersect. These angles are always supplementary.
In the figure above, ∠1 and ∠2 form a linear pair and are supplementary. Therefore, ∠1 + ∠2 = 180°.
12.2. Angles on a Straight Line
When multiple angles lie on a straight line, their measures add up to 180 degrees.
For example, if angles A, B, and C lie on a straight line, then:
∠A + ∠B + ∠C = 180°
12.3. Interior Angles on the Same Side of a Transversal
When a transversal intersects two parallel lines, the interior angles on the same side of the transversal are supplementary.
In the figure above, ∠3 and ∠6 are interior angles on the same side of the transversal and are supplementary. Similarly, ∠4 and ∠5 are supplementary.
13. Interactive Exercises to Reinforce Learning
Engage with these interactive exercises to solidify your understanding of supplementary angles:
- Identify Supplementary Angles: Given a set of angle pairs, identify which pairs are supplementary.
- Find the Missing Angle: Given one angle, calculate its supplement.
- Solve for Unknown Variables: Use supplementary angle relationships to solve for unknown variables in geometric diagrams.
- Real-World Applications: Apply your knowledge of supplementary angles to solve practical problems in architecture, engineering, and navigation.
- Create Your Own Problems: Challenge yourself by creating your own supplementary angle problems and solving them.
14. Frequently Asked Questions (FAQs) About Supplementary Angles
| Question | Answer |
|---|---|
| Can two acute angles be supplementary? | No, because the sum of two acute angles (each less than 90°) will always be less than 180°. |
| Can two obtuse angles be supplementary? | No, because the sum of two obtuse angles (each greater than 90°) will always be greater than 180°. |
| Can two right angles be supplementary? | Yes, because 90° + 90° = 180°. |
| Are supplementary and complementary angles the same? | No, supplementary angles add up to 180°, while complementary angles add up to 90°. |
| What type of angle is formed when supplementary angles are joined? | A straight angle (180°) is formed. |
| What is a linear pair? | A linear pair is a pair of adjacent, supplementary angles formed by two intersecting lines. |
| What is the supplement of a 45-degree angle? | The supplement is 180° – 45° = 135°. |
| How are supplementary angles used in real-world applications? | They are used in architecture, engineering, navigation, and construction to ensure structural integrity and accurate measurements. |
| What is the Supplementary Angle Theorem? | If two angles are supplementary to the same angle, then those two angles are congruent. |
| Can non-adjacent angles be supplementary? | Yes, angles do not need to be adjacent to be supplementary; they simply need to add up to 180°. |
15. The Importance of Mastering Supplementary Angles
Mastering the concept of supplementary angles is crucial for success in geometry and related fields. It provides a foundation for understanding more complex geometric relationships and problem-solving techniques. By thoroughly understanding supplementary angles, you can:
- Solve a wide range of geometry problems.
- Apply geometric principles to real-world applications.
- Develop strong critical thinking and problem-solving skills.
- Build a solid foundation for advanced math courses.
- Enhance your spatial reasoning abilities.
16. How WHAT.EDU.VN Can Help You Learn More
At WHAT.EDU.VN, we’re dedicated to providing clear, comprehensive, and accessible educational resources. If you have any questions or need further clarification on supplementary angles or any other topic, don’t hesitate to reach out.
Our platform offers:
- Detailed Articles: In-depth explanations of various mathematical and scientific concepts.
- Practice Problems: A wide range of practice problems to test your knowledge and skills.
- Interactive Exercises: Engaging exercises to reinforce learning and understanding.
- Expert Support: Access to experts who can answer your questions and provide guidance.
- Free Question Answering: A free service to ask any question and receive prompt, accurate answers.
17. Ask Your Questions on WHAT.EDU.VN
Still have questions? Visit WHAT.EDU.VN today and ask your questions for free. Our community of experts is ready to provide the answers and support you need to succeed.
Understanding supplementary angles is just the beginning. With WHAT.EDU.VN, you can explore a vast array of topics and unlock your full learning potential.
18. Need Help? Contact Us
If you need further assistance or have any questions, please don’t hesitate to contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
Let what.edu.vn be your guide to mastering supplementary angles and beyond.
