What Is A Variable In Math? Understanding Variables

What Is A Variable In Math? It’s a fundamental question. At WHAT.EDU.VN, we break down mathematical concepts to make learning easy and accessible for everyone. Discover how variables play a crucial role in algebra, calculus, and beyond. Learn more about mathematical expressions, algebraic equations, and problem-solving strategies.

1. Definition of a Variable in Math

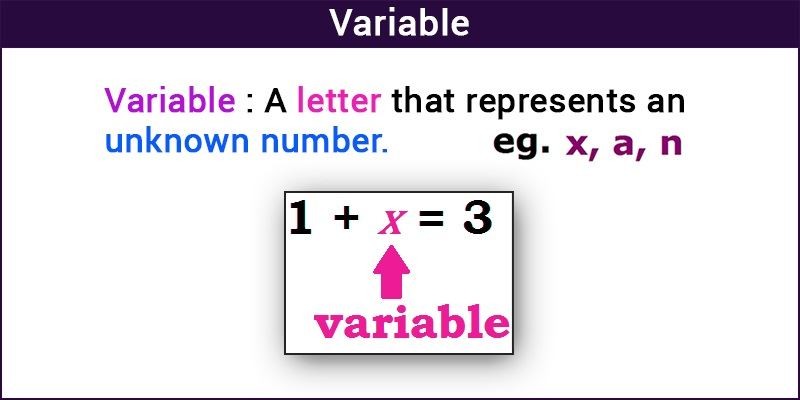
A variable in mathematics is a symbol, typically a letter, that represents a value that is unknown or that can change. Variables are fundamental to algebra and are used to express relationships between quantities. They allow us to formulate general rules and solve for unknown values in equations and inequalities.

Variables can represent a wide range of values, including numbers, quantities, or even other mathematical objects. The key characteristic of a variable is its ability to take on different values, making it a versatile tool for mathematical modeling and problem-solving.

1.1. The Role of Variables in Equations

In equations, variables act as placeholders for unknown values. The goal is often to determine the value(s) of the variable(s) that make the equation true. This process is known as solving the equation.

For example, in the equation x + 5 = 10, x is a variable representing an unknown number. Solving the equation involves finding the value of x that satisfies the equation, which in this case is x = 5.

1.2. Variables in Expressions

Variables are also used in mathematical expressions, which are combinations of numbers, variables, and operations. Unlike equations, expressions do not have an equals sign and cannot be “solved.” Instead, expressions can be simplified or evaluated for specific values of the variables.

For example, in the expression 3x + 2y, x and y are variables. If we assign values to x and y, such as x = 2 and y = 3, we can evaluate the expression:

3(2) + 2(3) = 6 + 6 = 12

1.3. Why Variables Are Important

Variables are essential in mathematics for several reasons:

• Generalization: They allow us to express mathematical relationships and rules in a general form that applies to a wide range of specific cases.
• Problem-Solving: They enable us to represent unknown quantities and solve for them using algebraic techniques.
• Modeling: They are used to create mathematical models of real-world phenomena, allowing us to analyze and make predictions.
• Abstraction: They promote abstract thinking and the ability to manipulate mathematical concepts without relying on specific numerical values.

2. Types of Variables in Math

Variables in math can be classified based on their role and behavior within equations, expressions, and functions. Understanding these different types of variables is crucial for effectively working with mathematical concepts.

2.1. Independent Variables

An independent variable is a variable whose value is not determined by other variables in the equation or function. It is the input or the variable that is manipulated or changed to observe its effect on other variables.

In a function y = f(x), x is typically the independent variable. The value of x can be chosen freely, and the function f determines the corresponding value of the dependent variable y.

For example, in the equation y = 2x + 3, x is the independent variable. We can choose any value for x, and the equation will determine the corresponding value of y.

2.2. Dependent Variables

A dependent variable is a variable whose value is determined by the value of one or more independent variables. It is the output or the variable that is being measured or observed in response to changes in the independent variable.

In a function y = f(x), y is typically the dependent variable. Its value depends on the value of x chosen.

For example, in the equation y = 2x + 3, y is the dependent variable. Its value depends on the value of x. If x = 1, then y = 2(1) + 3 = 5.

2.3. Control Variables

In experimental settings, control variables are variables that are kept constant to prevent them from influencing the relationship between the independent and dependent variables. These variables are carefully monitored and maintained to ensure that the observed effects are due to the independent variable alone.

For example, in an experiment to test the effect of fertilizer on plant growth, control variables might include the amount of water given to each plant, the type of soil used, and the amount of sunlight each plant receives.

2.4. Constants

While not variables themselves, constants are often used in conjunction with variables in mathematical expressions and equations. A constant is a fixed value that does not change. Constants can be numbers, such as 2, 3.14 (pi), or mathematical symbols, such as e (Euler’s number).

In the equation y = 2x + 3, 2 and 3 are constants. The value of y depends on the variable x and these fixed constants.

2.5. Parameters

Parameters are values that are fixed for a particular context but can vary in different contexts. They are often used in equations and functions to represent specific characteristics or conditions.

For example, in the equation of a line y = mx + b, m and b are parameters. m represents the slope of the line, and b represents the y-intercept. While x and y are variables that can take on different values, m and b are fixed for a particular line but can change to define a different line.

3. Examples of Variables in Different Math Contexts

Variables are used extensively in various branches of mathematics. Here are some examples of how variables are used in different contexts:

3.1. Algebra

In algebra, variables are used to represent unknown quantities in equations and inequalities. Algebraic expressions are manipulated to solve for the value(s) of the variables that satisfy the given conditions.

Example:

Solve for x in the equation 3x - 5 = 7.

1. Add 5 to both sides: 3x = 12
2. Divide both sides by 3: x = 4

In this example, x is the variable, and the goal is to find the value of x that makes the equation true.

3.2. Calculus

In calculus, variables are used to represent quantities that change continuously. Calculus deals with rates of change and accumulation, and variables are essential for expressing these concepts.

Example:

Find the derivative of the function f(x) = x^2 + 2x - 1.

The derivative, denoted as f'(x), represents the instantaneous rate of change of the function with respect to x.

f'(x) = 2x + 2

In this example, x is the variable, and the derivative f'(x) is another function that depends on the value of x.

3.3. Geometry

In geometry, variables are used to represent lengths, angles, areas, and volumes. Geometric formulas often involve variables that represent the dimensions of shapes.

Example:

Find the area of a rectangle with length l and width w.

The area A of the rectangle is given by the formula:

A = l * w

In this example, l and w are variables representing the length and width of the rectangle, respectively.

3.4. Statistics

In statistics, variables are used to represent data points or characteristics of a population. Statistical analysis involves examining the relationships between variables and drawing inferences about the population.

Example:

Consider a dataset of students’ test scores. The variable x might represent a student’s score on a particular test. Statistical measures, such as the mean and standard deviation, can be calculated for this variable to describe the distribution of test scores.

3.5. Trigonometry

In trigonometry, variables are used to represent angles and side lengths of triangles. Trigonometric functions, such as sine, cosine, and tangent, relate angles to the ratios of side lengths.

Example:

In a right triangle, let θ be an angle, opposite be the length of the side opposite to θ, and hypotenuse be the length of the hypotenuse.

The sine of θ is given by:

sin(θ) = opposite / hypotenuse

In this example, θ, opposite, and hypotenuse are variables, and the sine function relates the angle θ to the ratio of the side lengths.

4. Variables in Real-World Applications

Variables are not just abstract mathematical concepts; they are used extensively in real-world applications to model and solve problems in various fields.

4.1. Physics

In physics, variables are used to represent physical quantities such as distance, time, velocity, acceleration, force, and energy. Physical laws and equations relate these variables to describe the behavior of the physical world.

Example:

Newton’s second law of motion states that the force F acting on an object is equal to the mass m of the object multiplied by its acceleration a:

F = m * a

In this equation, F, m, and a are variables representing force, mass, and acceleration, respectively.

4.2. Engineering

In engineering, variables are used to represent design parameters, material properties, and performance characteristics. Engineering models and simulations use variables to analyze and optimize designs.

Example:

In electrical engineering, Ohm’s law relates the voltage V across a resistor to the current I flowing through it and the resistance R of the resistor:

V = I * R

In this equation, V, I, and R are variables representing voltage, current, and resistance, respectively.

4.3. Economics

In economics, variables are used to represent economic quantities such as price, quantity, income, and demand. Economic models use variables to analyze and predict economic behavior.

Example:

In a simple supply and demand model, P represents the price of a good, and Q represents the quantity of the good. The demand curve shows the relationship between P and Q from the consumer’s perspective, while the supply curve shows the relationship between P and Q from the producer’s perspective.

4.4. Computer Science

In computer science, variables are used to store data and information in computer programs. Variables are assigned names and data types, and their values can be manipulated during program execution.

Example:

In a Python program, you might declare a variable age to store a person’s age:

age = 30
print(age)  # Output: 30

In this example, age is a variable that stores the integer value 30.

4.5. Data Science

In data science, variables are used to represent features or attributes of a dataset. Data analysis and machine learning algorithms use variables to identify patterns and make predictions.

Example:

In a dataset of housing prices, variables might include the size of the house (in square feet), the number of bedrooms, the number of bathrooms, and the location of the house. These variables are used to build models that predict the price of a house based on its characteristics.

5. How to Work with Variables Effectively

Working with variables effectively is crucial for success in mathematics and related fields. Here are some tips for using variables effectively:

5.1. Choose Meaningful Variable Names

When working with variables in equations, expressions, or computer programs, choose names that are descriptive and meaningful. This makes your work easier to understand and reduces the risk of errors.

Example:

Instead of using x and y to represent the length and width of a rectangle, use length and width.

5.2. Understand the Context

Be aware of the context in which variables are being used. Different fields may have different conventions and interpretations for variables.

Example:

In physics, t typically represents time, while in statistics, t might represent a t-statistic.

5.3. Keep Track of Units

When working with variables that represent physical quantities, keep track of the units of measurement. This helps prevent errors and ensures that your results are meaningful.

Example:

If distance is measured in meters and time is measured in seconds, then velocity = distance / time will be measured in meters per second.

5.4. Use Variables to Generalize

Use variables to express mathematical relationships and rules in a general form. This allows you to apply these relationships to a wide range of specific cases.

Example:

The formula for the area of a circle, A = πr^2, uses the variable r to represent the radius of the circle. This formula applies to any circle, regardless of its size.

5.5. Practice Problem-Solving

Practice solving problems that involve variables. This helps you develop your skills in manipulating variables and applying mathematical concepts.

Example:

Solve for x in the equation 2x + 3 = 7.

1. Subtract 3 from both sides: 2x = 4
2. Divide both sides by 2: x = 2

6. Common Mistakes to Avoid When Working with Variables

Working with variables can sometimes be challenging, and it’s easy to make mistakes. Here are some common mistakes to avoid:

6.1. Confusing Variables with Constants

A common mistake is to confuse variables with constants. Remember that variables can take on different values, while constants have fixed values.

Example:

In the equation y = 2x + 3, x and y are variables, while 2 and 3 are constants.

6.2. Using the Same Variable for Different Quantities

Avoid using the same variable to represent different quantities in the same problem. This can lead to confusion and errors.

Example:

If you are working with two different rectangles, use different variables for their lengths and widths (e.g., l1, w1 for the first rectangle and l2, w2 for the second rectangle).

6.3. Not Defining Variables Clearly

Always define your variables clearly before using them. This includes specifying the quantity that the variable represents and the units of measurement.

Example:

Before using the variable t in a physics problem, state that t represents time in seconds.

6.4. Incorrectly Applying Algebraic Operations

Be careful when applying algebraic operations to equations and expressions that involve variables. Make sure you are following the correct order of operations and applying the same operations to both sides of an equation.

Example:

To solve for x in the equation 3x + 5 = 14, you must first subtract 5 from both sides before dividing by 3.

6.5. Forgetting to Check Your Answers

After solving for the value(s) of a variable, always check your answers by substituting them back into the original equation or problem. This helps ensure that your answers are correct.

Example:

If you solve for x in the equation 2x - 1 = 5 and get x = 3, substitute x = 3 back into the equation: 2(3) - 1 = 6 - 1 = 5. Since the equation is true, your answer is correct.

7. Advanced Concepts Related to Variables

As you progress in your mathematical studies, you will encounter more advanced concepts related to variables. Here are some examples:

7.1. Systems of Equations

A system of equations is a set of two or more equations that involve the same variables. The goal is to find the values of the variables that satisfy all of the equations simultaneously.

Example:

Solve the following system of equations:

x + y = 5
2x - y = 1

7.2. Functions of Several Variables

A function of several variables is a function that takes multiple inputs, each represented by a variable.

Example:

The volume V of a cylinder is a function of its radius r and height h:

V(r, h) = πr^2h

7.3. Linear Algebra

Linear algebra deals with vectors, matrices, and linear transformations. Variables are used to represent the components of vectors and matrices.

Example:

A vector v in two dimensions can be represented as:

v = [x, y]

where x and y are variables representing the components of the vector.

7.4. Differential Equations

Differential equations are equations that relate a function to its derivatives. Variables are used to represent the independent variable, the dependent variable, and the derivatives of the dependent variable.

Example:

The equation dy/dx = ky is a differential equation that describes exponential growth or decay.

7.5. Multivariable Calculus

Multivariable calculus extends the concepts of calculus to functions of several variables. It involves partial derivatives, multiple integrals, and vector calculus.

Example:

The gradient of a function f(x, y) is a vector that points in the direction of the greatest rate of increase of the function:

∇f = [∂f/∂x, ∂f/∂y]

8. Resources for Further Learning About Variables

If you want to learn more about variables in math, here are some resources that you may find helpful:

8.1. Online Courses

• Khan Academy: Offers free courses on algebra, calculus, and other math topics, with detailed explanations of variables.
• Coursera: Provides courses from top universities on various math subjects, including linear algebra and differential equations.
• edX: Offers courses on mathematics and statistics, with a focus on data analysis and modeling.
  

8.2. Textbooks

• “Algebra” by Michael Artin: A comprehensive textbook on abstract algebra, with a detailed treatment of variables and equations.
• “Calculus” by James Stewart: A widely used calculus textbook that covers variables, functions, derivatives, and integrals.
• “Linear Algebra and Its Applications” by David C. Lay: A clear and accessible introduction to linear algebra, with a focus on applications.

8.3. Websites

• WHAT.EDU.VN: Offers articles and resources on various math topics, including variables, equations, and functions.
• MathWorld: A comprehensive online encyclopedia of mathematics, with definitions, formulas, and examples.
• Wolfram Alpha: A computational knowledge engine that can solve equations, evaluate expressions, and provide information on math topics.

9. FAQ about Variables in Math

9.1. What is the difference between a variable and a constant?

A variable is a symbol that represents a value that can change, while a constant is a fixed value that does not change.

9.2. How do you solve for a variable in an equation?

To solve for a variable in an equation, you need to isolate the variable on one side of the equation by applying algebraic operations to both sides.

9.3. What are independent and dependent variables?

An independent variable is a variable whose value is not determined by other variables, while a dependent variable is a variable whose value depends on the value of one or more independent variables.

9.4. Can a variable represent a negative number?

Yes, a variable can represent a negative number, a positive number, zero, or any other type of number.

9.5. How are variables used in computer programming?

In computer programming, variables are used to store data and information in computer programs. Variables are assigned names and data types, and their values can be manipulated during program execution.

10. Need Help with Math? Ask Your Questions at WHAT.EDU.VN!

Are you struggling with math concepts? Do you have questions about variables, equations, or any other math topic? Don’t worry, we’re here to help!

At WHAT.EDU.VN, we provide a free platform for you to ask any question you have and receive answers from knowledgeable experts. Whether you’re a student, a professional, or just someone who’s curious about math, we’re here to support your learning journey.

10.1. Why Choose WHAT.EDU.VN?

• Free Service: Ask any question you have without paying a dime. We believe that everyone should have access to quality education.
• Fast Answers: Get answers to your questions quickly. Our community of experts is dedicated to providing timely and accurate responses.
• Knowledgeable Experts: Receive answers from experienced mathematicians, teachers, and professionals. Our experts have a deep understanding of math concepts and can provide clear and helpful explanations.
• Easy-to-Use Platform: Our website is designed to be user-friendly and accessible. Simply type your question and submit it to our community.
• Comprehensive Coverage: Get answers to questions on any math topic, from basic arithmetic to advanced calculus.

10.2. How to Ask a Question on WHAT.EDU.VN

1. Visit our website: WHAT.EDU.VN
2. Navigate to the “Ask a Question” section.
3. Type your question clearly and concisely.
4. Provide any relevant background information or context.
5. Submit your question.
6. Check back regularly for answers from our experts.

10.3. Contact Us

If you have any questions or feedback about our service, please don’t hesitate to contact us.

Address: 888 Question City Plaza, Seattle, WA 98101, United States
Whatsapp: +1 (206) 555-7890
Website: what.edu.vn

We are committed to providing a valuable resource for anyone who wants to learn more about math. Ask your questions today and let us help you succeed!