What Is A Vertex? Understanding Vertices In Geometry

What Is A Vertex? It’s a fundamental concept in geometry, representing a crucial point where lines or edges meet. At WHAT.EDU.VN, we simplify complex topics like this, offering clear explanations and solutions to all your questions. This comprehensive guide will explore the definition, properties, and applications of vertices, ensuring you grasp this essential geometric concept and encouraging you to ask further questions on related topics on WHAT.EDU.VN for expert insights. We’ll also cover the plural form: vertices and related terms.

1. Defining a Vertex: The Cornerstone of Geometric Shapes

A vertex, in its simplest form, is a point where two or more lines, curves, or edges meet. It’s a foundational element in defining shapes and structures, both in two-dimensional and three-dimensional spaces. Understanding what constitutes a vertex is crucial for comprehending the properties and characteristics of geometric figures.

Think of a vertex as the “corner” of a shape. For example, a square has four corners, and each of these corners is a vertex. Similarly, a triangle has three vertices, and a cube has eight.

Definition: A point where two or more lines, curves, or edges intersect.
Plural: Vertices
Importance: Crucial for defining shapes and understanding their properties.
Examples: Corners of a square, triangle, or cube.

2. Vertices in Two-Dimensional (2D) Shapes

In 2D geometry, a vertex is the point where two sides of a polygon meet. Polygons are closed shapes formed by straight line segments. The number of vertices in a polygon is always equal to the number of its sides.

Examples of 2D Shapes and Their Vertices

Shape	Number of Sides	Number of Vertices
Triangle	3	3
Square	4	4
Rectangle	4	4
Pentagon	5	5
Hexagon	6	6
Octagon	8	8

Alt text: Example of 2D shapes including a square, triangle, and polygon with labeled vertices where sides meet.

Polygons: Closed shapes formed by straight line segments.
Relationship: Number of vertices = Number of sides.
Examples: Triangles, squares, pentagons, hexagons.
Key takeaway: Each corner of a 2D polygon is a vertex.

3. Vertices in Three-Dimensional (3D) Shapes

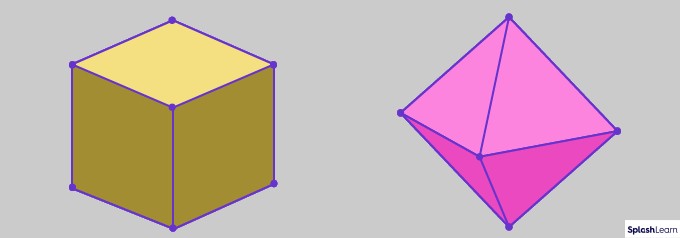
In 3D geometry, a vertex is the point where three or more edges of a solid meet. These solids, also known as polyhedra, are three-dimensional shapes with flat faces and straight edges. The vertices are the “corners” of these 3D objects.

Examples of 3D Shapes and Their Vertices

Shape	Number of Vertices
Cube	8
Cuboid	8
Tetrahedron	4
Square Pyramid	5
Octahedron	6

Alt text: Visual representation of a cube and an octahedron, highlighting the vertices as red dots.

Polyhedra: Three-dimensional shapes with flat faces and straight edges.
Vertices: Corners where edges meet.
Examples: Cubes, cuboids, tetrahedra, pyramids.
Key takeaway: The intersection of multiple edges forms a vertex in 3D shapes.

4. Distinguishing Vertices from Other Geometric Points

While vertices are essential points in geometry, it’s crucial to differentiate them from other types of points such as midpoints, centers, and points of tangency.

Point Type	Definition	Location	Example
Vertex	Point where two or more lines, curves, or edges meet	Corners of shapes	Corner of a square or a cube
Midpoint	Point that divides a line segment into two equal parts	Middle of a line segment	Center of a side of a triangle
Center	Point equidistant from all points on a circle or sphere	Middle of a circle or sphere	Center of a circle or a sphere
Point of Tangency	Point where a line or curve touches another curve or surface at one point	Where a tangent line touches a circle or curve	Where a tangent line touches a circle

Vertices: Corners where lines/edges meet.
Midpoints: Points dividing a line segment into two equal parts.
Centers: Points equidistant from all points on a circle or sphere.
Points of Tangency: Points where a line or curve touches another curve or surface.

5. Real-World Applications of Vertices

Vertices are not just abstract geometric concepts; they have numerous practical applications in various fields, including:

Architecture: Architects use vertices to design buildings and structures, ensuring stability and aesthetic appeal.
Computer Graphics: In computer graphics and animation, vertices define the shapes and forms of 3D models.
Engineering: Engineers use vertices in structural analysis to determine the stress and strain on various components of a structure.
Mapping and Navigation: Vertices are used in mapping and navigation systems to represent key locations and intersections.
Game Development: Game developers use vertices to create realistic and interactive environments and characters.

Alt text: An architectural drawing displaying vertices used in designing a house plan.

Architecture: Design of stable and aesthetically pleasing buildings.
Computer Graphics: Defining shapes and forms of 3D models.
Engineering: Structural analysis and stress determination.
Mapping: Representing key locations and intersections.
Game Development: Creating realistic environments and characters.

6. How to Identify Vertices in Different Shapes

Identifying vertices in different shapes is a fundamental skill in geometry. Here’s how you can do it:

Look for Corners: In 2D shapes, vertices are typically the corners where the sides meet.
Count the Sides: The number of vertices in a polygon is equal to the number of its sides.
Identify Intersections: In 3D shapes, vertices are the points where multiple edges intersect.
Visualize the Shape: Mentally visualize the shape and identify the points that form its corners or edges.
Use Tools: Use geometric tools like rulers and protractors to accurately locate and identify vertices.

Corners: Identify corners in 2D shapes.
Side Count: Relate the number of sides to the number of vertices.
Edge Intersections: Find points where multiple edges intersect in 3D shapes.
Visualization: Mentally picture the shape and locate corners.
Tools: Use rulers and protractors for accurate identification.

7. Common Mistakes to Avoid When Identifying Vertices

When working with vertices, it’s important to avoid common mistakes that can lead to incorrect results. Here are some pitfalls to watch out for:

Confusing Vertices with Midpoints: Vertices are corners, while midpoints are points on a line segment.
Miscounting Vertices: Ensure you accurately count the number of vertices in a shape, especially in complex 3D figures.
Ignoring Hidden Vertices: In 3D shapes, some vertices may be hidden from view.
Assuming All Shapes Have Vertices: Shapes like circles and spheres do not have vertices.
Overlooking Vertices in Irregular Shapes: Irregular shapes may have vertices that are not immediately obvious.

Distinguish: Differentiate vertices from midpoints.
Accurate Count: Ensure precise counting, especially in 3D.
Hidden Points: Account for vertices hidden from view in 3D.
Shape Variety: Remember that not all shapes have vertices.
Irregular Forms: Pay attention to less obvious vertices in irregular shapes.

8. Advanced Concepts Related to Vertices

Vertices are also important in more advanced geometric concepts such as:

Graph Theory: Vertices are fundamental in graph theory, representing nodes in a network.
Linear Programming: Vertices represent feasible solutions in linear programming problems.
Computer-Aided Design (CAD): Vertices are used to define the geometry of complex 3D models.
Finite Element Analysis (FEA): Vertices are used to create meshes for analyzing stress and strain in structures.
Topology: Vertices are used to study the properties of shapes that are preserved under continuous deformations.

Graph Theory: Represent nodes in a network.
Linear Programming: Represent feasible solutions.
CAD: Define geometry of complex 3D models.
FEA: Create meshes for structural analysis.
Topology: Study shape properties under deformation.

9. Tips and Tricks for Mastering Vertex Concepts

To truly master the concept of a vertex, consider the following tips and tricks:

Practice Regularly: Work through a variety of exercises and problems involving vertices.
Visualize Shapes: Develop your ability to visualize shapes in both 2D and 3D.
Use Manipulatives: Use physical objects or software to manipulate shapes and identify vertices.
Relate to Real-World Examples: Look for examples of vertices in everyday objects and structures.
Seek Clarification: Don’t hesitate to ask questions and seek clarification when needed.

Consistent Study: Regular practice with vertex problems.
Spatial Skills: Enhance the ability to visualize shapes.
Hands-On Learning: Manipulate physical or digital shapes.
Practical Connections: Find vertices in everyday objects.
Ask Questions: Seek clarification when uncertain.

10. The Role of Vertices in Geometric Proofs

Vertices play a vital role in geometric proofs by providing specific points of reference for establishing relationships and properties. Here’s how:

Defining Angles: Vertices are used to define angles, which are essential for proving geometric theorems.
Establishing Congruence: Vertices are used to establish congruence between shapes by comparing corresponding sides and angles.
Determining Similarity: Vertices are used to determine similarity between shapes by comparing ratios of corresponding sides.
Constructing Auxiliary Lines: Vertices are used to construct auxiliary lines that help prove geometric theorems.
Identifying Key Points: Vertices serve as key points for applying geometric principles and theorems.

Angle Definitions: Defining angles for geometric proofs.
Congruence: Establishing shape congruence through vertices.
Similarity: Determining shape similarity using vertex ratios.
Auxiliary Lines: Constructing lines for theorem proofs.
Key Points: Identifying vertices for geometric principles.

11. Importance of Understanding Vertices in Standardized Tests

A solid understanding of vertices is crucial for success in standardized tests such as the SAT, ACT, and GRE. These tests often include questions that require you to identify, analyze, and apply vertex-related concepts.

Geometric Reasoning: Questions involving vertices test your ability to reason geometrically and solve problems involving shapes and angles.
Spatial Visualization: Questions involving 3D shapes test your ability to visualize objects in three dimensions and identify vertices.
Problem Solving: Questions involving vertices require you to apply geometric principles and formulas to solve real-world problems.
Critical Thinking: Questions involving vertices challenge you to think critically and analyze complex geometric scenarios.
Time Management: Mastering vertex concepts can help you solve problems more quickly and efficiently, saving valuable time on standardized tests.

Geometric Skills: Assessing geometric reasoning and problem-solving.
Spatial Ability: Testing 3D visualization and vertex identification.
Practical Application: Applying geometric principles to real-world problems.
Analytical Skills: Challenging critical thinking in complex scenarios.
Efficient Solving: Improving problem-solving speed for time management.

12. Vertices in Computer Science

Vertices play a critical role in computer science, particularly in areas like computer graphics, data structures, and algorithms.

Computer Graphics: Vertices are fundamental in creating 3D models and rendering scenes. They define the shape and structure of objects, and their properties (such as color and normal vectors) determine how these objects appear when lit and viewed.
Data Structures: In graph theory, which is a key area of computer science, a graph is a collection of vertices (or nodes) and edges that connect them. Graphs are used to model many real-world systems, such as social networks, transportation networks, and the internet.
Algorithms: Many algorithms operate on graphs, and vertices are often the starting point for these algorithms. For example, algorithms for finding the shortest path between two points in a network often start at a specific vertex and explore the graph until the destination vertex is reached.
Game Development: Vertices are used extensively in game development to create characters, environments, and special effects. Game engines use vertices to define the shape of 3D objects, and developers can manipulate these vertices to create animations and other visual effects.
Virtual Reality (VR) and Augmented Reality (AR): In VR and AR applications, vertices are used to create immersive and interactive experiences. They define the shape of virtual objects, and their properties determine how these objects interact with the real world.

Alt text: A visual representation of graph theory showcasing vertices and edges.

3D Modeling: Using vertices to form and render objects.
Graph Structures: Applying vertices in data structure graphs.
Pathfinding: Utilizing vertices as algorithm starting points.
Game Elements: Employing vertices to design game components.
Immersive Tech: Creating interactive VR and AR experiences.

13. Exploring Types of Vertices

Vertices aren’t all the same; they can be classified into different types based on their properties and the shapes they form.

Convex Vertex: A vertex in a polygon where the interior angle is less than 180 degrees. In other words, the vertex “points outward.”
Concave Vertex: A vertex in a polygon where the interior angle is greater than 180 degrees. This means the vertex “points inward.”
Regular Vertex: A vertex in a regular polygon, where all sides and angles are equal.
Irregular Vertex: A vertex in an irregular polygon, where sides and angles are not all equal.
Isolated Vertex: In graph theory, a vertex with no incident edges.
Leaf Vertex: In tree structures, a vertex with degree 1 (i.e., connected to only one other vertex).

Understanding these different types of vertices can help in analyzing and classifying geometric shapes more effectively.

Outward Point: Convex vertices with angles less than 180°.
Inward Point: Concave vertices with angles greater than 180°.
Equal Attributes: Regular vertices in polygons with equal sides.
Unequal Attributes: Irregular vertices in polygons with unequal sides.
Standalone Node: Isolated vertices with no connections in graphs.
Terminal Point: Leaf vertices connected to one other vertex in trees.

14. Practical Exercises to Strengthen Understanding

To reinforce your understanding of vertices, try these practical exercises:

Drawing Shapes: Draw various 2D shapes (triangles, squares, pentagons, hexagons) and label their vertices.
Identifying Vertices in Objects: Look around your environment and identify objects with vertices (e.g., a table, a book, a picture frame).
Building 3D Models: Use materials like cardboard or modeling clay to build simple 3D models (cubes, pyramids) and count their vertices.
Solving Puzzles: Work on puzzles that involve geometric shapes and vertices.
Using Software: Use geometry software to explore and manipulate shapes and vertices.

These exercises will help you develop a more intuitive understanding of vertices and their properties.

Shape Creation: Draw and label vertices on 2D figures.
Real-World Scavenger Hunt: Locate vertex-featuring objects around you.
Hands-On Creation: Construct 3D models and count their vertices.
Mind Bending Fun: Solve vertex-related puzzles.
Digital Exploration: Use software to manipulate vertex shapes.

15. The Significance of Vertices in Higher Mathematics

In higher mathematics, vertices are fundamental in various fields, including topology, differential geometry, and algebraic geometry.

Topology: Vertices are used to define the structure of topological spaces, which are spaces that are studied without regard to their exact shape or size.
Differential Geometry: Vertices are used to define the curvature of surfaces, which is a measure of how much a surface deviates from being flat.
Algebraic Geometry: Vertices are used to define algebraic varieties, which are sets of solutions to polynomial equations.

Understanding vertices is essential for anyone pursuing advanced studies in mathematics.

Space Definition: Defining topological structures with vertices.
Curvature Measurement: Assessing surface curvature with vertices.
Solution Definition: Defining algebraic equation solutions with vertices.

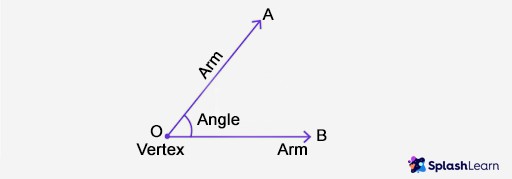
16. How Vertices Relate to Angles

Vertices are intrinsically linked to angles. An angle is formed by two rays or lines that share a common endpoint, and this endpoint is the vertex of the angle.

Formation of Angles: Vertices are the points where angles are formed.
Measurement of Angles: The size of an angle is determined by the amount of rotation between the two rays or lines that form the angle.
Types of Angles: Angles can be classified into different types (acute, right, obtuse, straight) based on their measure.

Understanding the relationship between vertices and angles is crucial for solving geometric problems.

Point of Origin: Vertices act as the origin for angle formation.
Size Determination: Rotation between lines determines angle size.
Angle Categorization: Angles classified by acute, right, etc., types.

17. Vertices and Their Role in Tessellations

Tessellations, also known as tilings, are patterns formed by repeating shapes that cover a plane without gaps or overlaps. Vertices play a crucial role in tessellations.

Arrangement of Shapes: The way shapes are arranged in a tessellation is determined by the properties of their vertices.
Angle Sum at Vertices: The sum of the angles around each vertex in a tessellation must be 360 degrees.
Types of Tessellations: Tessellations can be classified into different types (regular, semi-regular, irregular) based on the shapes used and the arrangement of vertices.

Understanding the role of vertices in tessellations can help in designing and analyzing these patterns.

Shape Arrangement: Vertex properties determine tiling arrangements.
Full Rotation: Vertex angles sum to 360 degrees in tilings.
Tiling Classification: Patterns categorized by shape and vertex.

18. Fun Facts About Vertices

Here are some fun facts about vertices that you might find interesting:

The word “vertex” comes from the Latin word “vertex,” which means “highest point” or “summit.”
The concept of a vertex has been studied for thousands of years, dating back to ancient Greek mathematicians.
Vertices are used in art and design to create visually appealing compositions.
Vertices are used in cryptography to create secure codes and ciphers.
Vertices are used in music theory to analyze the structure of musical compositions.

Origin Meaning: Vertex from Latin means “highest point.”
Ancient Study: Greeks studied vertices thousands of years ago.
Artistic Use: Used to create appealing visual compositions.
Security Applications: Employed in creating secure codes.
Musical Analysis: Utilized in analyzing musical structures.

19. How to Teach the Concept of a Vertex to Children

Teaching the concept of a vertex to children can be fun and engaging. Here are some tips:

Use Visual Aids: Use pictures, diagrams, and models to illustrate the concept of a vertex.
Relate to Real-World Objects: Point out vertices in everyday objects (e.g., corners of a book, points of a star).
Play Games: Play games that involve identifying and counting vertices.
Use Manipulatives: Use building blocks or other manipulatives to create shapes and identify vertices.
Keep It Simple: Use simple language and avoid technical jargon.

By making the learning experience fun and interactive, you can help children develop a solid understanding of vertices.

Engage Visually: Use pictures and models to illustrate vertices.
Everyday Connections: Point out vertices in daily objects.
Gamify Learning: Play vertex-related games.
Hands-On Approach: Use blocks to create shapes.
Simple Communication: Use clear, jargon-free language.

20. Frequently Asked Questions (FAQs) about Vertices

Question	Answer
What is a vertex?	A vertex is a point where two or more lines, curves, or edges meet.
What is the plural of vertex?	The plural of vertex is vertices.
Do all shapes have vertices?	No, not all shapes have vertices. For example, circles and spheres do not have vertices because they do not have straight edges or corners.
How do you identify a vertex?	Look for the point where two or more lines, curves, or edges meet.
What is the difference between a vertex and a midpoint?	A vertex is a corner of a shape, while a midpoint is the point that divides a line segment into two equal parts.
Can a shape have more than one vertex?	Yes, most shapes have more than one vertex. For example, a triangle has three vertices, a square has four vertices, and a cube has eight vertices.
How are vertices used in real life?	Vertices are used in architecture, computer graphics, engineering, mapping, and game development.
What is a convex vertex?	A convex vertex is a vertex in a polygon where the interior angle is less than 180 degrees.
What is a concave vertex?	A concave vertex is a vertex in a polygon where the interior angle is greater than 180 degrees.
How do vertices relate to angles?	Vertices are the points where angles are formed. An angle is formed by two rays or lines that share a common endpoint, and this endpoint is the vertex of the angle.

Still have questions? Don’t hesitate to ask our experts at WHAT.EDU.VN for more in-depth explanations and assistance! We are located at 888 Question City Plaza, Seattle, WA 98101, United States. Contact us on Whatsapp: +1 (206) 555-7890, or visit our website: WHAT.EDU.VN.

Conclusion

Understanding what is a vertex is fundamental to grasping geometry and its many applications. From defining the corners of simple shapes to playing a crucial role in advanced mathematical concepts and computer science, vertices are essential. By mastering the concepts discussed, you’ll be well-equipped to tackle geometric problems and appreciate the beauty and precision of mathematics.

Are you struggling to find quick and free answers to your questions? Do you feel lost and don’t know where to turn for reliable information? Are you worried about the cost of getting expert advice? Look no further! WHAT.EDU.VN offers a free platform where you can ask any question and receive prompt, accurate, and easy-to-understand answers. Our knowledgeable community is ready to help you with any topic, big or small.

Don’t let your curiosity be stifled. Visit what.edu.vn today and experience the ease and convenience of getting your questions answered for free! Ask your question now! Our team is ready to provide the support and guidance you need.