Are you looking for a simple explanation of what a vertex is in geometry? WHAT.EDU.VN is here to help you understand this fundamental concept with clear definitions and examples. We provide a free and easy-to-use platform for all your geometry questions, covering topics like corners, points, and intersections.
Table of Contents
1. What Is a Vertex?
2. What Are the Key Features of a Vertex?
3. What Are the Properties of a Vertex?
4. Vertex in 2D Shapes
5. Vertex in 3D Shapes
6. How to Identify Vertices in Different Shapes
7. Real-World Examples of Vertices
8. Common Mistakes to Avoid When Identifying Vertices
9. Advanced Concepts Related to Vertices
10. Frequently Asked Questions (FAQs) About Vertices
1. What Is a Vertex?
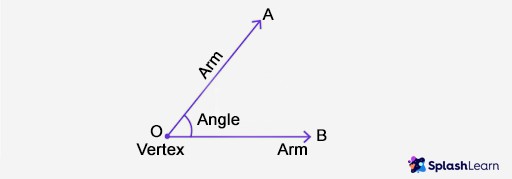
A vertex, in geometry, is a point where two or more lines, curves, or edges meet. Think of it as a corner. This point is crucial for defining the shape and structure of geometric figures, whether in two dimensions (2D) or three dimensions (3D). The term “vertex” comes from Latin, meaning “summit” or “peak,” which accurately describes its position at the highest or most prominent point of an angle or shape. In simpler terms, a vertex is where the sides of a shape connect. According to Euclidean Geometry, a vertex serves as a foundational element in understanding more advanced geometric concepts.
2. What Are the Key Features of a Vertex?
Understanding the key features of a vertex will help you identify and work with them more effectively.
2.1 Meeting Point
A vertex is primarily a meeting point. It is where two or more lines, line segments, or rays intersect. This intersection forms an angle. For example, in a triangle, the three corners are the vertices, each formed by the meeting of two sides.
2.2 Angle Formation
Vertices are always associated with angles. The angle is formed by the two lines or edges that meet at the vertex. The size of the angle can vary, but the presence of an angle is a defining feature of a vertex.
2.3 Dimensionality
Vertices exist in both 2D and 3D shapes. In 2D shapes, vertices are the corners of polygons. In 3D shapes, vertices are the points where edges or faces meet. For example, a cube has eight vertices, each formed by the intersection of three edges.
2.4 Singular and Plural Forms
It’s important to use the correct terminology. The singular form is “vertex,” while the plural form is “vertices.” Knowing this helps in clear communication when discussing geometry.
2.5 Location
The location of a vertex is specific and fixed. It is the precise point where the lines or edges meet. This fixed position is essential for defining the shape accurately.
3. What Are the Properties of a Vertex?
Understanding the properties of a vertex is crucial for grasping its role in geometry. Here are some key properties to consider.
3.1 No Sides, No Vertex
If a shape doesn’t have straight sides or edges, it doesn’t have vertices. For example, a circle, sphere, or cylinder doesn’t have vertices because they lack straight edges that meet at a point.
3.2 Angle Formation
When lines meet at a point to form a vertex, they also create an interior angle. This angle is an integral part of the shape. The vertex is the point where this angle is formed.
3.3 Intersection
Vertices are always points of intersection. They mark where different parts of a shape come together. Whether it’s the sides of a polygon or the edges of a polyhedron, the vertex is the point of convergence.
3.4 Importance in Shape Definition
Vertices play a critical role in defining the shape of geometric figures. The number and arrangement of vertices determine the type of shape. For instance, a triangle is defined by its three vertices, and a square is defined by its four vertices.
3.5 Use in Calculations
Vertices are used in various calculations, such as finding the area and volume of shapes. They serve as reference points in coordinate geometry, making it easier to perform mathematical operations.
4. Vertex in 2D Shapes
In two-dimensional shapes, a vertex is the point where two sides of the shape meet. Understanding how vertices are present in different 2D shapes is essential for geometry.
4.1 Polygons
Polygons are closed 2D shapes with straight sides. Each corner of a polygon is a vertex. Here are a few examples:
- Triangle: A triangle has three sides and three vertices.
- Square: A square has four sides and four vertices.
- Rectangle: A rectangle also has four sides and four vertices.
- Pentagon: A pentagon has five sides and five vertices.
- Hexagon: A hexagon has six sides and six vertices.
4.2 Circles
A circle does not have any vertices because it has no straight sides. It is a continuous curve.
4.3 Other 2D Shapes
Any 2D shape with straight sides will have vertices. The number of vertices depends on the number of sides. For example, a quadrilateral (a four-sided shape) will have four vertices.
4.4 Importance
Understanding vertices in 2D shapes helps in calculating area, perimeter, and other geometric properties. It also helps in recognizing and classifying different shapes.
5. Vertex in 3D Shapes
In three-dimensional shapes, a vertex is a point where three or more edges or faces meet. These points define the corners of 3D objects.
5.1 Polyhedra
Polyhedra are 3D shapes with flat faces and straight edges. Each corner of a polyhedron is a vertex. Here are some examples:
- Cube: A cube has six faces, twelve edges, and eight vertices.
- Cuboid: A cuboid (rectangular prism) also has six faces, twelve edges, and eight vertices.
- Pyramid: A pyramid has a base and triangular faces that meet at a single vertex (apex). The number of vertices depends on the shape of the base. For example, a square pyramid has five vertices.
- Prism: A prism has two identical ends and flat sides. The number of vertices depends on the shape of the ends. For example, a triangular prism has six vertices.
5.2 Spheres and Cylinders
A sphere and a cylinder do not have any vertices because they do not have flat faces or straight edges.
5.3 Importance
Understanding vertices in 3D shapes is essential for calculating volume, surface area, and other spatial properties. It also helps in visualizing and constructing 3D models.
5.4 Euler’s Formula
Euler’s formula relates the number of vertices (V), edges (E), and faces (F) of a polyhedron: V – E + F = 2. This formula is a fundamental concept in topology and is useful for verifying the properties of polyhedra.
6. How to Identify Vertices in Different Shapes
Identifying vertices in different shapes is a fundamental skill in geometry. Here’s how you can do it effectively.
6.1 Visual Inspection
The simplest way to identify a vertex is by visual inspection. Look for the corners or points where lines or edges meet. This method works well for simple shapes like triangles, squares, and cubes.
6.2 Counting Sides and Corners
For polygons and polyhedra, count the number of sides and corners. Each corner is a vertex. For example, a hexagon has six sides and six vertices.
6.3 Using Definitions
Refer to the definitions of different shapes. For example, a triangle is defined as a shape with three sides and three vertices. Use this definition to confirm that a shape is indeed a triangle and to identify its vertices.
6.4 Coordinate Geometry
In coordinate geometry, vertices can be identified by their coordinates. Each vertex is a point in space, defined by its x, y, and z coordinates. Use these coordinates to locate and identify vertices accurately.
6.5 Practice
The more you practice identifying vertices, the easier it becomes. Work with different shapes and objects to sharpen your skills.
7. Real-World Examples of Vertices
Vertices are not just abstract geometric concepts. They appear in many real-world objects and structures. Recognizing them can help you appreciate the practical applications of geometry.
7.1 Buildings
Buildings often have vertices where walls meet. The corners of a room or the points where the roof meets the walls are examples of vertices.
7.2 Furniture
Furniture items like tables and chairs have vertices. The corners of a table or the points where the legs of a chair connect to the seat are vertices.
7.3 Bridges
Bridges, especially truss bridges, have many vertices where the structural members meet. These vertices are crucial for the stability and strength of the bridge.
7.4 Crystals
Crystals have distinct geometric shapes with well-defined vertices. The points where the faces of a crystal meet are vertices.
7.5 Everyday Objects
Many everyday objects, such as boxes, books, and toys, have vertices. Recognizing these vertices helps in understanding the shape and structure of these objects.
8. Common Mistakes to Avoid When Identifying Vertices
Identifying vertices can sometimes be tricky, and it’s easy to make mistakes. Here are some common errors to avoid.
8.1 Confusing Edges and Vertices
Edges are the lines or curves that connect vertices. Don’t confuse edges with vertices, which are the points where edges meet.
8.2 Counting Curves as Vertices
Shapes like circles and spheres do not have vertices. Avoid mistakenly identifying points on a curve as vertices.
8.3 Miscounting Vertices
When counting vertices, be systematic and double-check your count. It’s easy to miss a vertex or count one twice, especially in complex shapes.
8.4 Ignoring Hidden Vertices
In 3D shapes, some vertices may be hidden from view. Remember to account for these hidden vertices when identifying all the vertices of a shape.
8.5 Overlooking Small Angles
Vertices are always associated with angles, but sometimes the angle can be very small or obtuse.
9. Advanced Concepts Related to Vertices
Once you have a solid understanding of the basics, you can explore more advanced concepts related to vertices.
9.1 Graph Theory
In graph theory, a vertex (or node) is a fundamental concept. Graphs are used to model relationships between objects, and vertices represent these objects.
9.2 Topology
Topology is a branch of mathematics that studies the properties of shapes that are preserved under continuous deformations. Vertices play a crucial role in topological analysis.
9.3 Linear Programming
Linear programming involves optimizing a linear objective function subject to linear constraints. Vertices of the feasible region are often the solutions to these problems.
9.4 Computer Graphics
In computer graphics, vertices are used to define 3D models. The position and properties of vertices determine the shape and appearance of the model.
9.5 Finite Element Analysis
Finite element analysis (FEA) is a numerical method used to solve engineering and mathematical problems. Vertices are used to discretize the domain and create a mesh for analysis.
10. Frequently Asked Questions (FAQs) About Vertices
Here are some frequently asked questions about vertices to help reinforce your understanding.
10.1 How Many Vertices Does a Cone Have?
A cone has one vertex at its apex.
10.2 How Many Vertices Does a Cube Have?
A cube has eight vertices.
10.3 Which Objects Do Not Have a Vertex?
Objects without straight edges or angles do not have a vertex. Examples include circles, spheres, and cylinders.
10.4 How Many Vertices Does a Tetrahedron Have?
A tetrahedron has four vertices. It also has six edges and four triangular faces.
10.5 Can a Shape Have an Infinite Number of Vertices?
No, shapes with straight sides have a finite number of vertices. Shapes without straight sides, like circles, do not have any vertices.
10.6 What Is the Significance of Vertices in Real Life?
Vertices are essential in various fields, including architecture, engineering, and computer graphics. They help define the structure and shape of objects and are used in calculations for stability, design, and analysis.
10.7 How Do You Find the Coordinates of a Vertex?
The coordinates of a vertex can be found using coordinate geometry. Each vertex is a point in space defined by its x, y, and z coordinates. These coordinates can be determined by measuring the position of the vertex relative to a reference point.
10.8 What Is the Difference Between a Vertex and an Edge?
A vertex is a point where lines or edges meet, while an edge is a line segment or curve that connects two vertices. They are distinct but related components of geometric shapes.
10.9 Why Is Understanding Vertices Important in Geometry?
Understanding vertices is crucial because they are fundamental to defining and analyzing shapes. They are used in various calculations and are essential for recognizing and classifying different geometric figures.
10.10 Where Can I Learn More About Vertices?
You can learn more about vertices through textbooks, online courses, and educational websites like WHAT.EDU.VN. Practice identifying vertices in different shapes and explore advanced concepts to deepen your understanding.
Geometry is a critical part of mathematics that forms a large part of the curriculum for students. Advanced learning of geometry is possible only with the correct understanding of the basics of geometry. Vertex is one of the preliminary topics that make the foundation of Geometry.
Do you have more questions about vertices or any other geometry topics? Don’t hesitate to ask on WHAT.EDU.VN, where you can get free and fast answers from experts and peers. Our platform is designed to help you understand complex concepts easily.
Ready to Explore More?
Have more questions or need further clarification on any topic? Visit what.edu.vn today and ask your question for free! Our community of experts and learners is ready to assist you. Get the answers you need quickly and easily. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States or via WhatsApp at +1 (206) 555-7890.