What Is An Equation? Definition, Types, and Examples

Are you curious about what an equation is and how it works? WHAT.EDU.VN is here to provide you with a clear understanding of equations, their types, and practical examples. Let’s simplify the concept of equations together, ensuring you grasp the fundamentals for your mathematical journey. Discover the solution at WHAT.EDU.VN, where we break down complex topics into easy-to-understand explanations, covering everything from mathematical statements to algebraic expressions and problem-solving techniques.

1. Defining Equations: What Is An Equation?

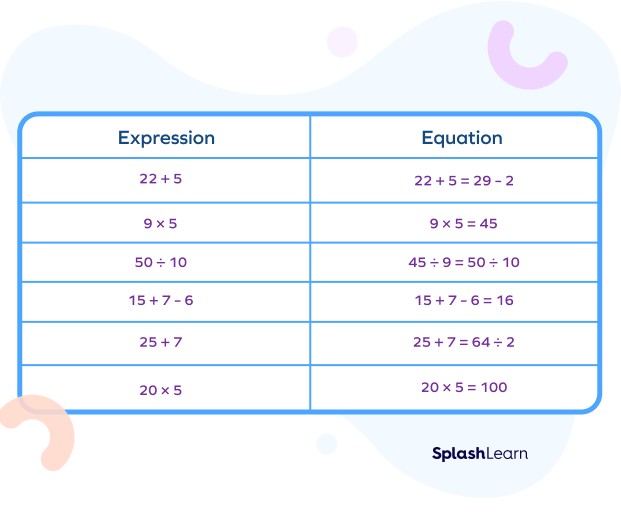
In its simplest form, What Is An Equation? It’s a mathematical statement showing that two expressions are equal. Think of it as a balanced scale, where both sides must weigh the same.

For example:

• 3x + 5 = 14
• 4y + 2 = 18
• 9m = 49.5

Here, expressions like “3x + 5” and “14” are separated by an equals sign (=), indicating they have the same value.

1.1 Equations vs. Expressions

It’s crucial to differentiate between an equation and an expression. An expression is a combination of numbers, variables, and operations, without an equals sign. An equation always has an equals sign, linking two expressions.

Examples of Expressions:

• k + 7
• u + w
• x³ + 5x
• 9t

Key Difference: Equations show equality; expressions do not.

1.2 Variables in Equations

Many algebraic equations contain variables, which are symbols (usually letters) representing unknown values. The goal is often to find the value of the variable that makes the equation true.

1.3 Why Are Equations Important?

Equations are fundamental to mathematics and are used extensively in various fields, including science, engineering, economics, and computer science. They allow us to model real-world situations, solve problems, and make predictions.

2. Types of Equations

Equations come in different forms, each with its unique characteristics and methods for solving. Here are some common types:

2.1 Linear Equations

What is a linear equation? A linear equation is one where the highest power of the variable is 1. These equations can have one or more variables. They are also known as one-degree equations.

General Form: ax + b = 0, where ‘a’ and ‘b’ are constants and ‘x’ is the variable.

Example: 2x + 3 = 7

Characteristics:

• Graph as a straight line.
• Easy to solve using basic algebraic operations.
• Have only one solution (in the case of one variable).

2.2 Quadratic Equations

What is a quadratic equation? A quadratic equation is a second-order equation. In quadratic equations, at least one of the variables should be raised to the exponent 2.

General Form: ax² + bx + c = 0, where ‘a’, ‘b’, and ‘c’ are constants and ‘x’ is the variable.

Example: x² + 3x + 2 = 0

Characteristics:

• Have a squared term (x²).
• Can have two, one, or no real solutions.
• Solved using factoring, completing the square, or the quadratic formula.

2.3 Cubic Equations

What is a cubic equation? A cubic equation is a third-order equation. In cubic equations, at least one of the variables should be raised to the exponent 3.

General Form: ax³ + bx² + cx + d = 0, where ‘a’, ‘b’, ‘c’, and ‘d’ are constants and ‘x’ is the variable.

Example: x³ – 6x² + 11x – 6 = 0

Characteristics:

• Have a cubed term (x³).
• Can have up to three real solutions.
• More complex to solve than linear or quadratic equations.

2.4 Rational Equations

What is a rational equation? A rational equation is an equation that contains fractions with a variable in the numerator, denominator, or both.

General Form: P(x)/Q(x) = 0, where P(x) and Q(x) are polynomials.

Example: x/2 = (x + 1)/4

Characteristics:

• Contain fractions with variables.
• Require careful handling to avoid dividing by zero.
• Solved by multiplying both sides by the least common denominator.

2.5 Other Types of Equations

Besides the common types mentioned above, there are many other types of equations, including:

• Exponential Equations: Equations where the variable is in the exponent (e.g., 2^x = 8).
• Logarithmic Equations: Equations involving logarithms (e.g., log₂(x) = 3).
• Trigonometric Equations: Equations involving trigonometric functions (e.g., sin(x) = 0.5).
• Differential Equations: Equations involving derivatives (used in calculus and advanced mathematics).

3. Understanding Solutions of Equations

The solution of an equation is the value (or values) of the variable that makes the equation a true statement. In other words, it’s the value that, when substituted into the equation, makes both sides equal.

3.1 Verifying Solutions

To verify whether a particular value is a solution, substitute it into the equation and check if both sides are equal.

Example 1: Verify that x = 3 is the solution of an equation 4x − 8 = − 5 + 3x

• Substitute x = 3 in the given equation
• LHS: 4x − 8 = 4(3) − 8 = 12 − 8 = 4
• RHS: −5 + 3x = −5 + 3(3) = −5 + 9 = 4
• LHS = RHS
• So, x = 3 is the solution of an equation 4x − 8 = −5 + 3x.

Example 2: Verify that y = −2 is the solution of an equation 2m – 4 = 1

• Substitute y = −2 in the given equation.
• LHS: 2m – 4 = 2(−2) − 4 = − 4 − 4 = − 8
• RHS: 1
• − 8 ≠ 1
• LHS ≠ RHS
• So, y = −2 is not the solution of given equation 2m – 4 = 1.

3.2 Multiple Solutions

Some equations, like quadratic equations, can have more than one solution. This means there are multiple values that make the equation true.

Example: x² – 5x + 6 = 0 has solutions x = 2 and x = 3

3.3 No Solution

Certain equations have no solution, meaning there is no value that can make the equation true.

Example: x + 1 = x + 2 (no value of x can satisfy this)

4. How to Solve Linear Equations with One Variable

Solving equations involves finding the value of the variable that makes the equation true. Here’s a step-by-step guide for solving linear equations with one variable:

4.1 Steps to Solve Linear Equations

1. Simplify: Remove parentheses, brackets, braces, and fraction bars by distributing or combining like terms on each side of the equation.
2. Isolate the Variable: Use addition or subtraction to move all terms with the variable to one side of the equation and all constant terms to the other side. Remember, whatever operation you perform on one side, you must do on the other side to maintain equality.
3. Solve for the Variable: Use multiplication or division to isolate the variable. This will give you the value of the variable that satisfies the equation.

4.2 Transposition Method

An alternative method is transposition, where any term of an equation may be taken from one side to the other with a change in its sign.

Example: 4a – 9 = 13 – 7a

1. Transpose −7a to LHS and − 9 to RHS: 4a + 7a = 13 + 9
2. Add like terms: 11a = 22
3. Transpose 11 to RHS: a = 22/11
4. Simplify: a = 2

4.3 Examples of Solving Linear Equations

Example 1: Solve for x: x + 8 = 12

• Subtract 8 from both sides: x + 8 – 8 = 12 – 8
• Simplify: x = 4

Example 2: Solve: (1/5) + 3w = (2/5)

1. Transpose (1/5) to RHS: 3w = (2/5) – (1/5)
2. Simplify: 3w = (1/5)
3. Transpose 3 to RHS: w = (1/5) / 3
4. Simplify: w = 1/15

5. Solved Examples On Equation

Let’s walk through some more examples to solidify your understanding.

Example 1: Solve for x.

x + 8 = 12

Solution:

Here is the equation to solve: x + 8 = 12

We need to leave x alone on one side of the equation. For this, we must take 8 out of both sides.

So, x + 8 – 8 = 12 – 8

or, x = 4

Example 2: Determine if the value 3 is a solution of the equation:

4x – 2 = 3x + 1

Solution:

We will substitute the value of 3 in this equation and will check if the left-side equation is equal to the right-hand side.

So,

4(3) – 2 = 3(3) + 1

or, 12 – 2 = 9 + 1

or, 10 = 10

Yes, 3 is a solution to the given equation.

Example 3: Solve the equation: 6(2x + 3) + x – 7 = 3(5x + 7) + 2x

Solution:

6(2x + 3) + x – 7 = 3(5x + 7) + 2x

Expanding the terms we get,

12x + 18 + x – 7 = 15x + 21 + 2x

or, 13x + 11 = 17x + 21

On further simplification,

13x – 17x = 21 – 11

−4x = 10

x = -$frac{10}{4}$

x = -$frac{5}{2}$

6. Real-World Applications of Equations

Equations are not just abstract mathematical concepts; they are powerful tools used to solve real-world problems. Here are a few examples:

6.1 Physics

In physics, equations are used to describe the motion of objects, the behavior of energy, and the properties of matter. For example, Newton’s second law of motion (F = ma) relates force, mass, and acceleration.

6.2 Engineering

Engineers use equations to design structures, circuits, and machines. For example, the equation for calculating the voltage drop across a resistor (V = IR) is fundamental in electrical engineering.

6.3 Economics

Economists use equations to model economic systems, predict market behavior, and analyze the impact of policies. For example, supply and demand equations are used to determine market equilibrium.

6.4 Computer Science

Computer scientists use equations to develop algorithms, model data, and solve computational problems. For example, equations are used in machine learning to train models and make predictions.

7. Practical Problems On Equation

7.1 Equation Problems

Test your knowledge with these quizzes.

Problem 1: Which of these is an equation?

• 7x + 5y = 19
• 5 – 2
• $frac{4}{7} – frac{2}{7}$
• 3a + 9b

Solution:

The correct answer is: 7x + 5y = 19. This is because option a has an equal sign (=) between two math expressions, making it an equation. The other options are expressions.

Problem 2: Determine the equation for which 7 is Not the solution.

• n + 2 = 9
• 7 – g = 0
• x – 4 = 3
• h$times$ 1 = 8

Solution:

The correct answer is: h$times$ 1 = 8. This is because 7$times$ 1 = 7 and 7 ≠ 8. So 7 is not the solution for the given equation.

Problem 3: Solve 9k = −27

• 3
• 2
• −3
• −1

Solution:

The correct answer is: −3. To solve, divide both sides by 9: k = -$frac{27}{9}$, which simplifies to k = -3.

8. Tips and Tricks for Mastering Equations

Mastering equations requires practice and a solid understanding of the underlying concepts. Here are some tips and tricks to help you succeed:

• Practice Regularly: The more you practice, the more comfortable you will become with solving equations.
• Understand the Basics: Make sure you have a strong foundation in basic algebra concepts, such as variables, expressions, and operations.
• Break Down Complex Problems: When faced with a complex equation, break it down into smaller, more manageable steps.
• Check Your Work: Always check your solutions by substituting them back into the original equation to make sure they are correct.
• Use Resources: Take advantage of available resources, such as textbooks, online tutorials, and study groups.
• Ask for Help: Don’t be afraid to ask for help from teachers, tutors, or classmates if you are struggling with a particular concept.

9. Common Mistakes to Avoid

When working with equations, it’s easy to make mistakes. Here are some common mistakes to avoid:

• Incorrectly Distributing: Make sure to distribute correctly when removing parentheses or brackets.
• Forgetting to Perform Operations on Both Sides: Remember to perform the same operation on both sides of the equation to maintain equality.
• Combining Unlike Terms: Only combine like terms (terms with the same variable and exponent).
• Dividing by Zero: Avoid dividing by zero, as it is undefined.
• Ignoring Signs: Pay close attention to signs (positive and negative) when performing operations.

10. FAQ: Equations Explained

10.1 What Are the Different Types of Equations?

There are three types of equations based on the degree: Linear equation, quadratic equation, and cubic equation.

10.2 How Are Linear Equations Used in Daily Life?

Linear equations are used to find wages based on hourly pay rates, speed, and medicine dosage based on the patient’s weight.

10.3 What Must An Equation Have?

An equation in algebra is a statement of equality that contains one or more unknown quantities or variables.

10.4 How Do You Solve Equations?

Solving Equations – A General Rule:

• Remove parentheses and combine like terms on each side of the equation.
• To isolate the variable term, you can use addition or subtraction.
• To solve for a variable, use multiplication or division.

11. Why Choose WHAT.EDU.VN for Your Questions?

Finding reliable and accurate answers to your questions can be challenging. At WHAT.EDU.VN, we understand the difficulties you face and offer a unique platform designed to provide quick and dependable solutions.

11.1 Challenges Addressed

• Difficulty Finding Answers: It can be frustrating to search endlessly for the information you need.
• Uncertainty About Sources: Not all online sources are trustworthy, and it’s hard to know who to ask.
• Cost Concerns: Professional consultations can be expensive, making it difficult to get expert advice.
• Platform Usability: Many platforms are complicated and hard to navigate, wasting your time.

11.2 How WHAT.EDU.VN Helps

WHAT.EDU.VN offers a free and easy-to-use platform where you can ask any question and receive fast, accurate answers. Our community of knowledgeable users and experts are ready to assist you with clear, helpful information.

11.3 Benefits of Using WHAT.EDU.VN

• Free Question Platform: Ask questions without any cost.
• Fast and Accurate Answers: Get reliable information quickly.
• Easy-to-Understand Explanations: Information is presented in a clear and accessible manner.
• Community Support: Connect with others to exchange knowledge.
• Free Consultation: Get free advice for simple issues.

12. Take Action: Ask Your Questions on WHAT.EDU.VN

Ready to get your questions answered? Don’t struggle alone. Visit WHAT.EDU.VN today and experience the ease and convenience of our free question-and-answer platform.

Ready to Ask?

1. Visit our website: WHAT.EDU.VN
2. Ask your question in the search bar.
3. Get fast, accurate answers from our community of experts.

Contact Us

If you have any questions or need assistance, feel free to reach out:

• Address: 888 Question City Plaza, Seattle, WA 98101, United States
• WhatsApp: +1 (206) 555-7890
• Website: WHAT.EDU.VN

Stop wondering and start learning. Join WHAT.EDU.VN now and get the answers you deserve.

13. Conclusion

Understanding what is an equation is crucial for anyone studying mathematics or related fields. Equations are fundamental tools used to model and solve problems in various areas of life. By learning the different types of equations, how to solve them, and their real-world applications, you can enhance your problem-solving skills and gain a deeper appreciation for the power of mathematics. Remember, practice makes perfect, so keep solving equations and exploring new mathematical concepts. With persistence and the right resources, you can master equations and unlock a world of possibilities. And don’t forget, what.edu.vn is here to help you with any questions you may have.