Constant of proportionality defines the relationship between two proportional quantities, and WHAT.EDU.VN is here to help you understand it better. This constant, often denoted as ‘k’, is crucial in understanding direct and inverse variations. Ready to dive in and explore the world of proportional relationships and unit rates?
1. Understanding Constant of Proportionality
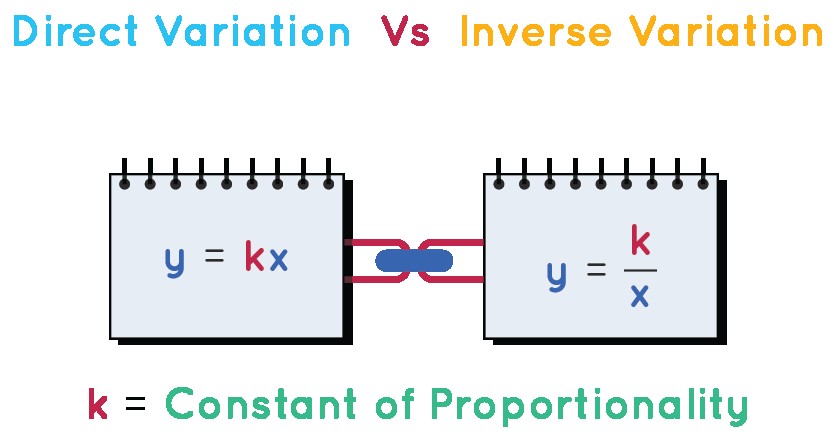
The constant of proportionality is a fixed value that describes the relationship between two quantities that are proportional to each other. This relationship can be either a direct variation or an inverse variation. Let’s break down each type:
1.1. Direct Variation
In direct variation, as one quantity increases, the other quantity also increases proportionally. The relationship is expressed as:
y = kxWhere:
yis one quantityxis the other quantitykis the constant of proportionality
This means that the ratio of y to x is always the same, which is k.
For example, if you’re buying apples and each apple costs $2, the total cost (y) is directly proportional to the number of apples you buy (x). The constant of proportionality (k) is $2.
1.2. Inverse Variation
In inverse variation, as one quantity increases, the other quantity decreases proportionally. The relationship is expressed as:
y = k/xWhere:
yis one quantityxis the other quantitykis the constant of proportionality
This means that the product of y and x is always the same, which is k.
For example, if you’re driving a certain distance, the time it takes (y) is inversely proportional to your speed (x). The constant of proportionality (k) is the distance.
1.3. Why is ‘k’ Called a Constant?
The term “constant” implies that the value of k does not change, regardless of the values of x and y. This unchanging nature of ‘k’ is what defines the proportional relationship between the two variables. Whether dealing with direct or inverse variation, identifying this constant is key to solving related problems.
2. Significance of Constant of Proportionality
The constant of proportionality isn’t just a number; it’s a key to understanding and solving real-world problems. It helps us to:
2.1. Determine Relationships
By finding the constant of proportionality, we can determine whether two variables have a direct or inverse relationship. This understanding is crucial in many fields, from science to economics.
2.2. Make Predictions
Once we know the constant of proportionality, we can predict how one variable will change when the other variable changes. This is useful for making informed decisions and planning.
2.3. Solve Problems
The constant of proportionality allows us to set up equations and solve for unknown quantities in proportional relationships. This is a fundamental skill in mathematics and many applied fields.
2.4. Real-World Applications
- Cooking: Scaling recipes up or down while maintaining the correct ratios of ingredients.
- Engineering: Designing structures and machines that maintain proportional relationships between different parts.
- Finance: Calculating interest rates and investment returns.
- Physics: Understanding relationships between physical quantities like force, mass, and acceleration.
3. Methods to Determine Constant of Proportionality
There are several ways to find the constant of proportionality, depending on the information you have:
3.1. Using Given Values
If you have specific values for both variables, you can use the appropriate equation to solve for k.
For direct variation (y = kx):
k = y/xFor inverse variation (y = k/x):
k = xyFor example, if y = 10 when x = 2 in a direct variation, then k = 10/2 = 5.
3.2. From a Table of Values
If you have a table of values for x and y, you can calculate the ratio y/x (for direct variation) or the product xy (for inverse variation) for each pair of values. If the ratio or product is the same for all pairs, then that value is the constant of proportionality.
| x | y | y/x |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 6 | 3 |
| 3 | 9 | 3 |

In this table, the constant of proportionality is 3.
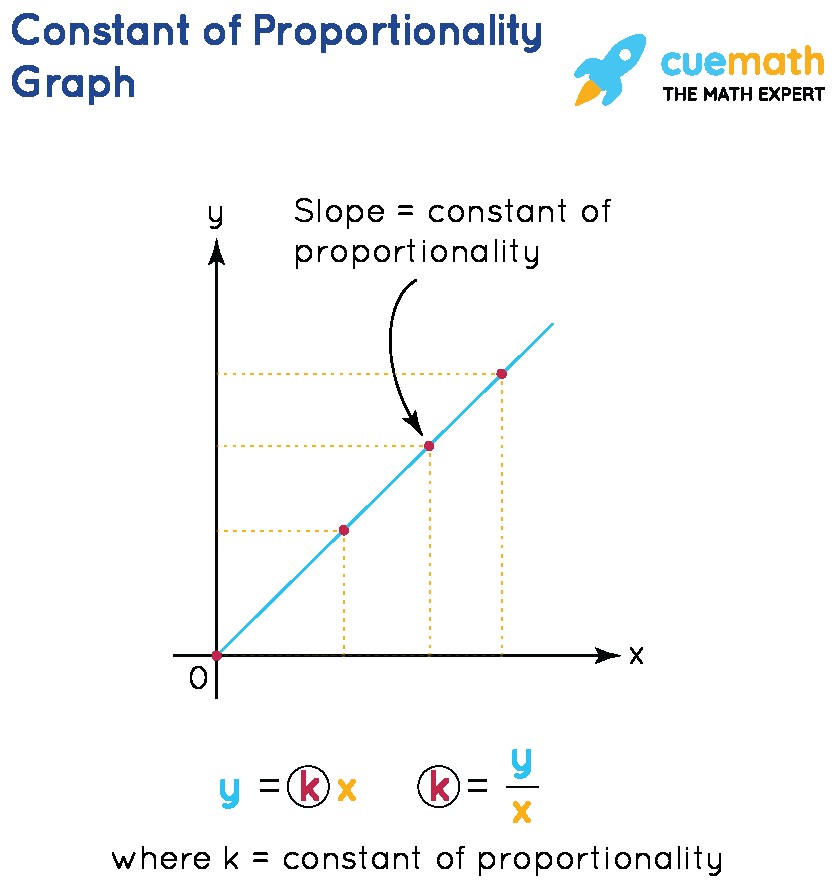
3.3. From a Graph
If you have a graph of the relationship between x and y, you can determine the constant of proportionality as follows:
- Direct Variation: The graph will be a straight line passing through the origin. The constant of proportionality is the slope of the line.
- Inverse Variation: The graph will be a hyperbola. You can find the constant of proportionality by choosing any point on the graph and calculating the product of its x and y coordinates.
4. Examples of Finding Constant of Proportionality
Let’s walk through some examples to illustrate how to find the constant of proportionality.
4.1. Example 1: Direct Variation
Suppose the distance a car travels (y) is directly proportional to the amount of fuel it consumes (x). If the car travels 150 miles on 5 gallons of fuel, find the constant of proportionality.
Using the direct variation equation y = kx, we have:
150 = k * 5Solving for k:
k = 150 / 5 = 30So, the constant of proportionality is 30 miles per gallon.
4.2. Example 2: Inverse Variation
The time it takes to complete a task (y) is inversely proportional to the number of workers (x). If 4 workers can complete the task in 6 hours, find the constant of proportionality.
Using the inverse variation equation y = k/x, we have:
6 = k / 4Solving for k:
k = 6 * 4 = 24So, the constant of proportionality is 24. This means the task requires 24 “worker-hours” of effort.
4.3. Example 3: Using a Table
Consider the following table showing the relationship between the number of hours worked (x) and the amount earned (y):
| Hours Worked (x) | Amount Earned (y) |
|---|---|
| 2 | 30 |
| 4 | 60 |
| 6 | 90 |
To find the constant of proportionality, calculate y/x for each pair of values:
- 30 / 2 = 15
- 60 / 4 = 15
- 90 / 6 = 15
Since the ratio is the same for all pairs, the constant of proportionality is 15 dollars per hour.
5. Common Mistakes to Avoid
When working with constant of proportionality, it’s important to avoid these common mistakes:
5.1. Confusing Direct and Inverse Variation
Make sure you correctly identify whether the relationship is direct or inverse before applying the appropriate formula.
5.2. Incorrectly Calculating ‘k’
Double-check your calculations when solving for k, especially when dealing with fractions or decimals.
5.3. Assuming Proportionality
Don’t assume that two variables are proportional without verifying the relationship using data or information.
5.4. Using the Wrong Units
Pay attention to the units of measurement and make sure they are consistent throughout the problem.
6. FAQs on Constant of Proportionality
6.1. What is the constant of proportionality also known as?
The constant of proportionality is also known as the unit rate.
6.2. How does the constant of proportionality relate to the slope of a line?
In direct variation, the constant of proportionality is the slope of the line when the relationship is graphed.
6.3. Can the constant of proportionality be negative?
Yes, the constant of proportionality can be negative, indicating an inverse relationship where one variable decreases as the other increases.
6.4. What are some real-world examples of constant of proportionality?
Real-world examples include the relationship between distance and time (at a constant speed), the relationship between the number of items and their total cost (at a constant price), and the relationship between the number of workers and the time it takes to complete a task (assuming each worker contributes equally).
6.5. How can I use the constant of proportionality to solve problems?
Once you know the constant of proportionality, you can use the appropriate equation (y = kx for direct variation, y = k/x for inverse variation) to solve for unknown quantities.
7. Practice Problems
Test your understanding with these practice problems:
-
The weight of an object on Earth (
y) is directly proportional to its mass (x). If an object with a mass of 10 kg weighs 98 N, find the constant of proportionality. -
The volume of a gas (
y) is inversely proportional to its pressure (x). If the volume of a gas is 5 L at a pressure of 2 atm, find the constant of proportionality. -
Determine if the following table represents a proportional relationship and, if so, find the constant of proportionality:
x y 1 4 2 8 3 12
8. Conclusion
Understanding the constant of proportionality is essential for grasping proportional relationships in mathematics and real-world scenarios. By correctly identifying the type of variation, calculating the constant, and avoiding common mistakes, you can confidently solve problems involving proportions.
Still have questions about constant of proportionality? Don’t hesitate to ask! At WHAT.EDU.VN, we provide a free platform for you to ask any question and receive quick, accurate answers from knowledgeable individuals. We are committed to making learning easy and accessible for everyone.
9. Need More Help? Ask Away at WHAT.EDU.VN
Are you struggling with understanding the constant of proportionality or any other math concept? Do you need a quick and reliable answer to a pressing question? Look no further than WHAT.EDU.VN!
9.1. Why Choose WHAT.EDU.VN?
- Free Access: Our platform is completely free to use. You can ask any question without worrying about subscription fees or hidden charges.
- Quick Answers: We understand the importance of timely information. Our community of experts and knowledgeable users are dedicated to providing prompt and accurate answers to your queries.
- Expert Guidance: Whether you’re a student, a professional, or simply a curious individual, you can benefit from the insights of experienced individuals in various fields.
- Easy to Use: Our platform is designed to be user-friendly and intuitive. You can easily post your questions and receive answers in a clear and organized manner.
- Diverse Topics: From mathematics and science to history and current events, you can ask questions on virtually any topic and receive insightful responses.
9.2. How to Ask a Question on WHAT.EDU.VN
- Visit Our Website: Go to WHAT.EDU.VN.
- Sign Up (Optional): While you can browse questions and answers without signing up, creating an account allows you to post questions and receive personalized notifications.
- Ask Your Question: Click on the “Ask a Question” button and type in your query. Be as specific as possible to ensure you receive a relevant and helpful answer.
- Submit Your Question: Once you’re satisfied with your question, submit it to the community.
- Receive Answers: Keep an eye on your question and check back for answers from our knowledgeable users.
9.3. Get in Touch
If you have any questions or need assistance, feel free to contact us:
- Address: 888 Question City Plaza, Seattle, WA 98101, United States
- WhatsApp: +1 (206) 555-7890
- Website: WHAT.EDU.VN
At WHAT.EDU.VN, we are dedicated to providing you with the resources and support you need to succeed. Ask your questions today and unlock a world of knowledge!
Don’t let confusion hold you back. Ask your questions now on what.edu.vn and get the answers you need to excel in your studies and beyond!
