What Is Exponential Function? Understanding Exponential Growth & Decay

Exponential functions are fundamental in mathematics and appear in numerous real-world applications. At WHAT.EDU.VN, we aim to provide a clear and comprehensive understanding of exponential functions, exploring their definition, formulas, graphs, properties, and applications. Let’s explore exponential increase, exponential decrease, and logarithmic functions.

This article dives deep into the world of exponential functions, explaining not just what they are but also how they work and why they’re important.

1. Defining the Exponential Function

An exponential function is a mathematical function defined by the formula:

f(x) = a^x

Where:

• ‘x’ is a variable representing any real number (the exponent).
• ‘a’ is a constant representing the base of the function.

Key Characteristics of the Base ‘a’:

• a > 0: The base must be a positive real number.
• a ≠ 1: The base cannot be equal to 1. If a=1, the function becomes f(x) = 1^x = 1, which is a constant function, not an exponential function.

Common Base:

The most frequently used base for exponential functions is the transcendental number e, also known as Euler’s number, approximately equal to 2.71828. When e is the base, the function is written as f(x) = e^x and is called the natural exponential function.

2. Understanding the Exponential Function Formula

The exponential function’s behavior is dictated by the formula f(x) = a^x. The ‘x’ in the exponent is what gives exponential functions their unique properties. The exponential curve visually represents this function and is significantly influenced by the value of ‘x’.

The core formula is:

f(x) = a^x

Where:

• f(x): Represents the value of the function for a given ‘x’.
• a: Is a constant (the base) where a > 0 and a ≠ 1.
• x: Is the variable, representing any real number.

Important Considerations:

• The function is undefined for negative bases when -1 < x < 1.
• Whether the curve grows or decays depends on the value of ‘a’ and the sign of ‘x’.

3. Exponential Growth vs. Exponential Decay

Exponential functions model situations where a quantity increases or decreases at a rate proportional to its current value. This leads to two distinct behaviors: exponential growth and exponential decay.

3.1. Exponential Growth

Exponential growth occurs when the quantity increases over time, starting slowly and then accelerating rapidly.

Formula for Exponential Growth:

y = a (1 + r)^x

Where:

• y: Final amount after time ‘x’.
• a: Initial amount.
• r: Growth rate (expressed as a decimal).
• x: Time interval.

In exponential growth, the rate of change increases over time, leading to a rapid, or “exponential,” increase. For example, if you invest money with compound interest, the amount you earn each year grows exponentially because it’s based on the increasing balance.

3.2. Exponential Decay

Exponential decay occurs when the quantity decreases over time, starting rapidly and then slowing down.

Formula for Exponential Decay:

y = a (1 – r)^x

Where:

• y: Final amount after time ‘x’.
• a: Initial amount.
• r: Decay rate (expressed as a decimal).
• x: Time interval.

In exponential decay, the rate of change decreases over time, leading to a gradual, or “exponential,” decrease. Radioactive decay is a classic example, where the amount of a radioactive substance decreases exponentially over time.

4. Visualizing Exponential Functions: The Graph

The graph of an exponential function provides a visual representation of its behavior, illustrating how the value of the function changes as the input ‘x’ varies. The steepness and direction of the curve reveal whether the function represents growth or decay.

The general form of the exponential function is y = a^x.

4.1. Key Observations from the Graph

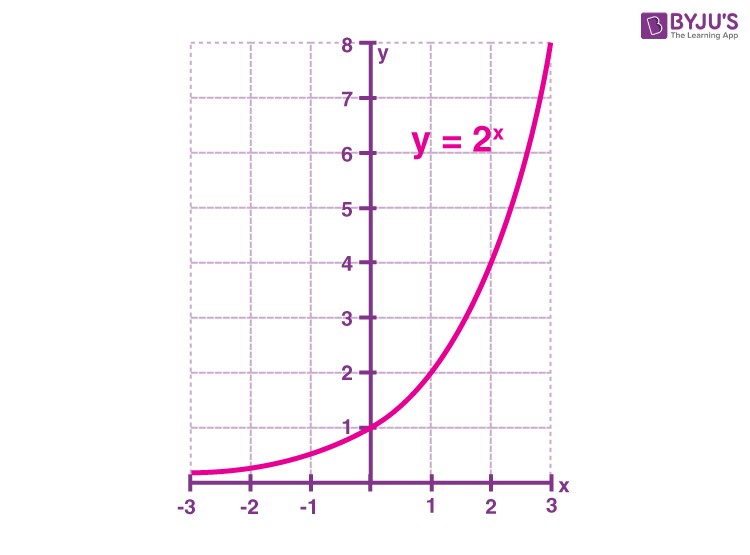
• Base Greater Than 1 (a > 1): The graph increases from left to right. As ‘x’ increases, ‘y’ increases exponentially. This represents exponential growth.
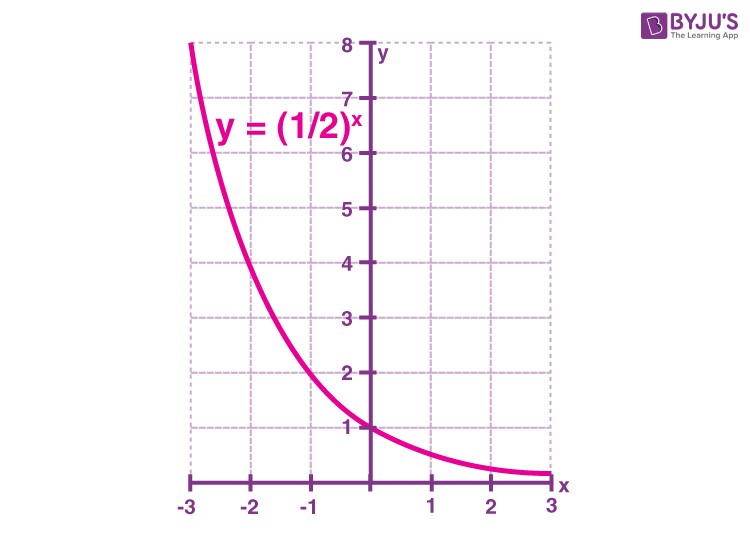
• Base Between 0 and 1 (0 < a < 1): The graph decreases from left to right. As ‘x’ increases, ‘y’ decreases exponentially, approaching zero. This represents exponential decay.
• The Point (0, 1): All exponential functions of the form y = a^x pass through the point (0, 1) because any number raised to the power of 0 equals 1 (a⁰ = 1).
• Asymptotic Behavior: Exponential functions approach the x-axis (y = 0) as a horizontal asymptote. In exponential growth, this occurs as x approaches negative infinity. In exponential decay, this occurs as x approaches positive infinity. This means the curve gets closer and closer to the x-axis but never actually touches it.

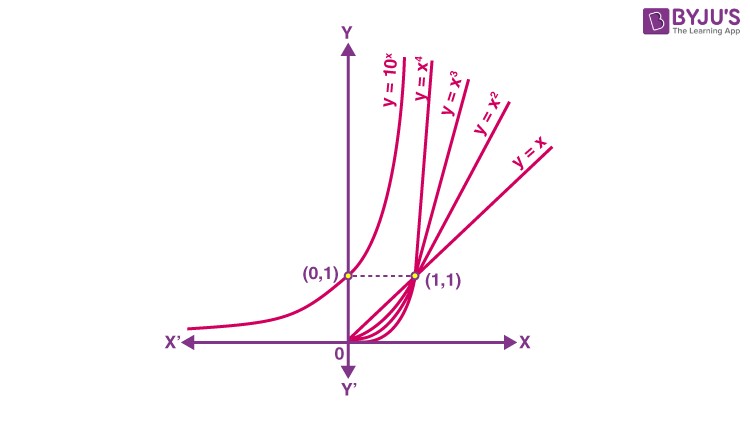
4.2. Impact of the Exponent

As the exponent increases, the curves on the graph become steeper, and the rate of growth increases accordingly. For x > 1, the value of y = fⁿ(x) increases for increasing values of (n).

Polynomial functions’ nature depends on their degree; the higher the degree, the greater the growth. An exponential function like y = f(x) = a^x (where a > 1) grows faster than any polynomial function. For any positive integers n, the function f(x) grows faster than fⁿ(x).

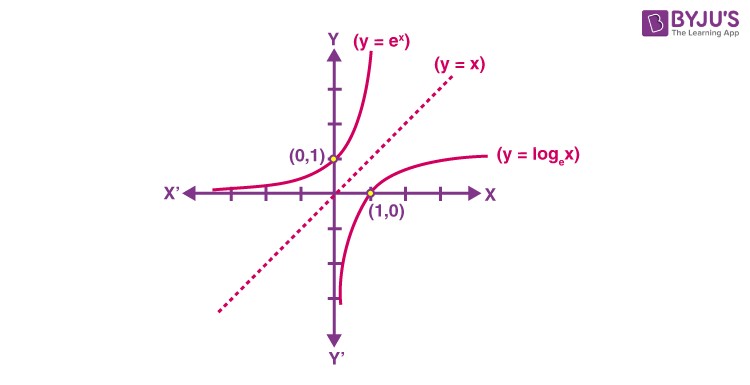
5. Logarithmic Functions: The Inverse of Exponential Functions

Logarithmic functions are closely related to exponential functions. In fact, they are inverse functions of each other. This means that a logarithm “undoes” an exponential function.

Definition:

For a > 1, the logarithm of b to base a is x if a^x = b. Mathematically, this is written as:

log_a b = x if a^x = b

This function is known as the logarithmic function.

5.1. Special Cases of Logarithms

• Common Logarithm: When the base is a = 10, it’s called the common logarithm, denoted as log₁₀ or simply log.
• Natural Logarithm: When the base is a = e (Euler’s number), it’s called the natural logarithm, denoted as ln.

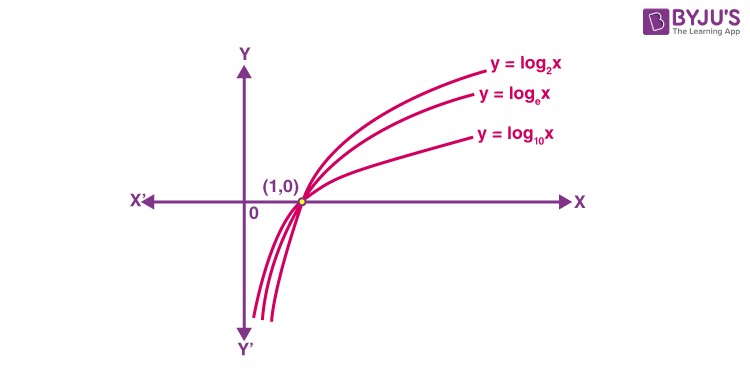
5.2. Key Observations about Logarithmic Functions (Base a > 1)

• Domain: The domain of a logarithmic function consists only of positive real numbers because we cannot take the logarithm of a negative number or zero.
• Range: The range of a logarithmic function is the set of all real numbers.
• Increasing Behavior: When you plot the graph of a logarithmic function and move from left to right, the function increases.
• Asymptotic Behavior: The graph of a logarithmic function never intersects the y-axis, although it seems to approach it.

5.3. Important Logarithmic Properties

• If log_ap = α, log_bp = β, and log_ba = µ, then a^α = p, b^β = p, and b^µ = a
• log_b(pq) = log_bp + log_bq
• log_b(p^y) = y log_bp
• log_b(p/q) = log_bp – log_bq

6. The Derivative of Exponential Functions

In calculus, the derivative of a function measures its rate of change. The derivative of an exponential function has a unique property.

The derivative of e^x with respect to x is e^x:

d(e^x)/dx = e^x

This means that the exponential function f(x) = e^x is its own derivative:

f'(x) = e^x = f(x)

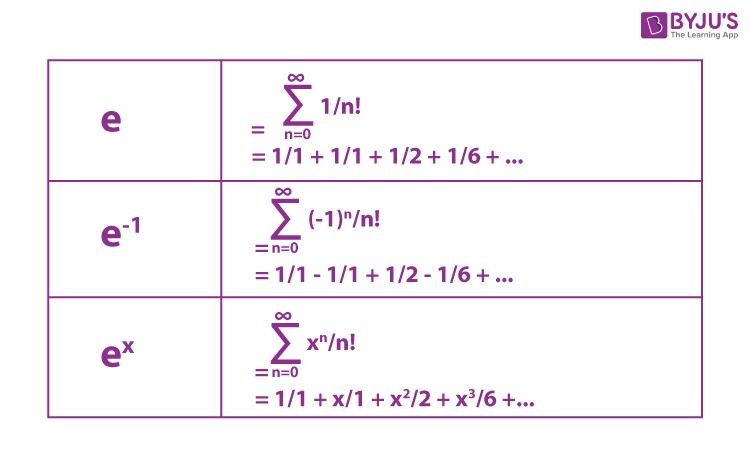
7. Exponential Series

An exponential series is an infinite sum of terms involving exponents. A common exponential series is:

8. Key Properties of Exponential Functions

The properties of exponential functions can be understood by examining their graphs. Let’s consider the exponential function y = 2^x as an example.

8.1. Properties when the Base is Greater Than 1 (a > 1)

• The graph passes through the point (0, 1).
• The domain is all real numbers.
• The range is y > 0.
• The graph is increasing (from left to right).
• The graph is asymptotic to the x-axis as x approaches negative infinity.
• The graph increases without bound as x approaches positive infinity.
• The graph is continuous.
• The graph is smooth (no sharp corners or breaks).

8.2. Properties when the Base is Between 0 and 1 (0 < a < 1)

Now consider the function y = 2^-x.

• The graph passes through the point (0, 1).
• The domain is all real numbers.
• The range is y > 0.
• The graph is decreasing (from left to right).
• The graph is asymptotic to the x-axis as x approaches positive infinity.
• The graph increases without bound as x approaches negative infinity.
• The graph is continuous.
• The graph is smooth.

9. Essential Rules for Working with Exponents

Understanding and applying exponent rules is crucial when working with exponential functions. These rules simplify expressions and allow you to solve exponential equations.

If a > 0 and b > 0, the following rules hold true for all real numbers x and y:

• Product of Powers: a^x * a^y = a^x+y
• Quotient of Powers: a^x / a^y = a^x-y
• Power of a Power: (a^x)^y = a^xy
• Power of a Product: a^xb^x = (ab)^x
• Power of a Quotient: (a/b)^x = a^x/b^x
• Zero Exponent: a⁰ = 1
• Negative Exponent: a^-x = 1/a^x

10. Examples of Exponential Functions

Here are some examples of exponential functions:

• f(x) = 2^x
• f(x) = (1/2)^x = 2^-x
• f(x) = 2^x+3
• f(x) = 0.5^x

11. Solved Problems: Applying Exponential Function Concepts

Let’s work through a couple of examples to solidify your understanding of exponential functions.

Question 1:

Simplify the exponential function 2^x – 2^x+1

Solution:

Given exponential function: 2^x – 2^x+1

Using the property: a^x * a^y = a^x+y

We can write 2^x+1 as 2^x * 2

So, the given function becomes:

2^x – 2^x+1 = 2^x – 2^x * 2

Now, factor out the term 2^x

2^x – 2^x+1 = 2^x – 2^x * 2 = 2^x(1 – 2)

2^x – 2^x+1 = 2^x(-1)

2^x – 2^x+1 = – 2^x

Therefore, the simplification of the given exponential function 2^x – 2^x+1 is – 2^x.

Question 2:

Solve the exponential equation: (¼)^x = 64

Solution:

Given exponential equation is:

(¼)^x = 64

Using the exponential rule (a/b)^x = a^x/b^x, we get:

1^x/4^x = 4³

1/4^x = 4³ [since 1^x = 1]

(1)(4^-x) = 4³

4^-x = 4³

Here, bases are equal.

So, by equating the powers, we have:

x = -3

12. Frequently Asked Questions (FAQ) About Exponential Functions

Question	Answer
What is the basic form of an exponential function?	The basic form is f(x) = ax, where ‘a’ is the base and ‘x’ is the exponent. The base ‘a’ must be positive and not equal to 1.
How do exponential growth and decay differ?	Exponential growth represents an increase in quantity over time, while exponential decay shows a decrease. Growth occurs when the base ‘a’ is greater than 1, and decay happens when ‘a’ is between 0 and 1.
What role does ‘e’ play in exponential functions?	‘e’ (Euler’s number) is a special base approximately equal to 2.71828. The function f(x) = ex is known as the natural exponential function and is frequently used in calculus and various applications.
What is the derivative of ex?	The derivative of ex with respect to x is simply ex itself, meaning the function is its own derivative.
What are the key properties of exponential graphs?	Key properties include passing through the point (0, 1), having a domain of all real numbers, a range of positive numbers, increasing or decreasing behavior based on the base, and asymptotic behavior approaching the x-axis.
How are logarithmic functions related to exponential functions?	Logarithmic functions are the inverse of exponential functions. The logarithm of a number ‘b’ to base ‘a’ is the exponent to which ‘a’ must be raised to equal ‘b.’
What are the common rules for manipulating exponents?	Common rules include the product of powers (ax * ay = ax+y), the quotient of powers (ax / ay = ax-y), the power of a power ((ax)y = axy), and others, which simplify expressions and solve equations.
Can exponential functions model real-world phenomena?	Yes, exponential functions are used extensively to model population growth, radioactive decay, compound interest, and many other real-world phenomena where quantities increase or decrease at a rate proportional to their current value.
How do you solve exponential equations?	Solving exponential equations often involves using logarithms to isolate the variable in the exponent. You can also use properties of exponents to simplify the equation before solving.
What is the difference between exponential and polynomial growth?	Exponential growth increases at a rate proportional to the current value, leading to rapid acceleration. Polynomial growth increases at a steady rate based on the degree of the polynomial but is eventually overtaken by exponential growth.

13. Further Practice

1. Graph an exponential function (⅓)^x – 1.
2. Solve for x: 8(4^x-1) = 4^5x
3. Solve the exponential equation for x: -5^x-3 = 25/40

Conclusion

Exponential functions are essential mathematical tools for modeling growth and decay in various real-world scenarios. Whether you are calculating compound interest, understanding population dynamics, or studying radioactive decay, the principles of exponential functions apply. By understanding the formulas, graphs, and properties of these functions, you can gain valuable insights into the world around you.

Do you have more questions about exponential functions or other math topics? Visit WHAT.EDU.VN today to ask your questions and receive free answers from our community of experts! Our mission is to provide quick, accurate, and easy-to-understand information to anyone seeking knowledge. Contact us at 888 Question City Plaza, Seattle, WA 98101, United States. Whatsapp: +1 (206) 555-7890. Visit our website what.edu.vn for more information.